There is nothing in the nature of music itself to determine the pitch of the tonic of any composition. If different melodies and musical pieces have to be executed by musical instruments or singing voices of definite compass, the tonic must be chosen of a suitable pitch, differing when the melody rises far above the tonic and when it sinks much below it. In short, the pitch of the tonic must be chosen so as to bring the compass of the tones of the piece within the compass of the executants, vocal or instrumental. This inevitable practical necessity entails the condition of being able to give any required pitch to the tonic.
Moreover, in the longer pieces of music, it is necessary to be able to make a temporary change of tonic, that is, to modulate, in order to avoid uniformity and to utilise the musical effects resulting from changing and then returning to the original key. Just as consonances are made more prominent and effective by means of dissonances, the feeling for the predominant tonality and the satisfaction which arises from it, is heightened by previous deviations into adjacent keys. The variety in musical turns produced by modulational connection has become all the more necessary for modern music, because we have been obliged entirely to renounce, or at any rate materially to circumscribe, the old principle of altering expression by means of the various tonal modes. The Greeks had a free choice among seven different tonal modes, the middle ages among five or six, but we can choose between two only, major and minor. Those old tonal modes presented a series of different degrees of tonal character, out of which two only remain suitable for harmonic music. But the clearer and firmer construction of an harmonic piece gives modern composers greater freedom in modulational deviations from the original key, and places at their command new sources of musical wealth, which were scarcely accessible to the ancients.
Finally I must just touch on the question, so much discussed, whether each different key has a peculiar character of its own.
It is quite clear that, within the course of a single piece of music, modulational deviations into the more or less distantly related keys on the dominant or subdominant side produce very different effects. This, however, arises simply from the contrast they offer to the original principal key, and would be merely a relative character. But the question here mooted is, whether individual keys have an absolute character of their own, independently of their relation to any other key.
This is often asserted, but it is difficult to determine how much truth the assertion contains, or even what it precisely means, because probably a variety of different things are included under the term character, and perhaps the amount of effect due to the particular instrument employed has not been allowed for. If an instrument of fixed tones is completely and uniformly tuned according to the equal temperament, so that all Semitones throughout the scale have precisely the same magnitude, and if also the musical quality of all the tones is precisely the same, there seems to be no ground for understanding how each different key should have a different character. Musicians fully capable of forming a judgment have also admitted to me, that no difference in the character of the keys can be observed on the organ, for example. And Hauptmann,[1] I think, is right when he makes the same assertion for singing voices with or without an organ accompaniment. A great change in the pitch of the tonic can at most cause all the higher notes to be strained or all the lower ones obscured.
On the other hand, there is a decidedly different character in different keys on pianofortes and bowed
instruments.
In bowed instruments the more powerful quality of tone in the open strings is conspicuous, and there are also probably differences in the quality of tone of strings which are stopped at short and long lengths, and these may alter the character of the key according to the degree of the scale on which they fall. This assumption is confirmed by the inquiries I have made of musicians respecting the mode in which they recognise keys under certain conditions. The inequality of intonation will add to this effect. The Fifths of the open strings are perfect Fifths. But it is impossible that all the other Fifths should be perfect if in playing in different keys each note has the same sound throughout, as appears at least to be the intention of elementary instruction on the violin. In this way the scales of the various keys will differ in intonation, and this will necessarily have a much more important influence on the character of the melody. [See App. XX. sect. G. arts. 6 and 7.]
The differences in quality of tone of different notes on wind instruments are still more striking.
If this view is correct, the character of the keys would be very different on different instruments, and I believe this to be the case. But it is a matter to be decided by a musician with delicate ears, who directs his attention to the points here raised.
It is, however, not impossible that by a peculiarity of the human ear, already touched upon in p. 116a, certain common features may enter into the character of keys,
independent of the difference of musical instruments, and dependent solely on the absolute pitch of the tonic. Since
All or some of these reasons, then, made it necessary for musicians to have free command over the pitch of the tonic, and hence even the later Greeks transposed their scales on to all degrees of the chromatic scale. For singers these transpositions offer no difficulties. They can begin with any required pitch, and find in their vocal instrument all such of the corresponding degrees as lie within the extreme limits of their voice. But the matter becomes much more difficult for musical instruments, especially for such as only possess tones of certain definite degrees of pitch. The difficulty is not entirely removed even on bowed instruments. It is true that these can produce every required degree of pitch; but players are unable to hit the pitch, as correctly as the ear desires, without acquiring a certain mechanical use of their fingers, which can only result from an immense amount of practice.
The Greek system was not accompanied with great difficulties, even for instruments, so long as no deviations into remote keys were permitted, and hence but few marks of sharps and flats had to be used. Up to the beginning of the seventeenth century musicians were content with two signs of depression for the notes \(B\flat\) and \(E\flat\), and with the sign \(\sharp\) for \(F\sharp\), \(C\sharp\), \(G\sharp\), in order to have the leading tones for the tonics \(G\), \(D\), and \(A\). They took care to avoid the enharmonically equivalent tones \(A\sharp\) for \(B\flat\), \(D\sharp\) for \(E\flat\), \(G\flat\) for \(F\sharp\), \(D\flat\) for \(C\sharp\), and \(A\flat\) for \(G\sharp\). By help of \(B\flat\) for \(B\)[3] every tonal mode could be transposed to the key of its subdominant, and no other transposition was made.
In the Pythagorean system, which maintained its predominance over theory to the time of Zarlino in the sixteenth century, tuning proceeded by ascending Fifths, thus —
Now if we tune two Fifths upwards and an Octave downwards, we make a step having the ratio \(\tfrac{3}{2}\times\tfrac{3}{2}\times\tfrac{1}{2}=\tfrac{9}{8}\), which is a major Second. This gives for the pitch of every second tone in the last list —
Now if we tune two Fifths upwards and an Octave downwards, we make a step having the ratio \(\tfrac{3}{2}\times\tfrac{3}{2}\times\tfrac{1}{2}=\tfrac{9}{8}\), which is a major Second. This gives for the pitch of every second tone in the last list —
Now if we proceed downwards by Fifths from \(C\) we obtain the series —
If we descend two Fifths and rise an Octave, we may obtain the tones —
Hence the tone \(B\sharp\) is higher than the Octave of \(C\) by the small interval
The tones in the upper line are all higher than those in the lower by the small interval \(\tfrac{73}{74}\) [ = 24 cents]. Our staff notation had its principles settled before the development of the modern musical system, and has consequently preserved these differences of pitch. But for practice on instruments with fixed tones the distinction between degrees of tone which lie so near to each other, was inconvenient, and attempts were made to fuse them together. This led to many imperfect attempts, in which individual intervals were more or less altered in order to keep the rest true, producing the so-called unequal temperaments, and finally to the system of equal temperament, in which the Octave was divided into 12 precisely equal degrees of tone.[4] We have seen that we can ascend from \(C\) by 12 perfect Fifths to \(B\sharp\), which differs from c by about \(\tfrac{1}{5}\) of a Semitone, namely by the interval \(\tfrac{73}{74}\). In the same way we can descend by 12 perfect Fifths to \(D\flat\flat\), which is as much lower than \(C\), as \(B\sharp\) is higher. If, then, we put \(C=B\sharp=D\flat\flat\), and distribute this little deviation of \(\tfrac{73}{74}\) equally among all the 12 Fifths of the circle, each Fifth will be erroneous by about \(\tfrac{1}{60}\) of a Semitone [or \(\tfrac{1}{11}\) of a comma or 2 cents], which is certainly a very small interval. By this means all varieties of tonal degrees within an Octave are reduced to 12, as on our modern keyed instruments.
The Fifth in the system of equal temperament, is, when expressed approximately in the smallest possible numbers,
\(=\tfrac{3}{2}\times\tfrac{885}{886}\). It is very seldom that any difficulty could result from its use in place of
the perfect Fifth. The root struck with its tempered Fifth makes one beat in the time that the Fifth makes
\(442\tfrac{1}{2}\) complete vibrations. Now since a makes 440 vibrations in a second, it follows that the tempered
Fifth
The Thirds and Sixths of the equal temperament are nearer the perfect intervals than are the Pythagorean.[5]
| Intervals | Perfect | Equally Tempered | Pythagorean | |||
| ratios | cents | ratios | cents | ratios | cents | |
| Major Third... |
|
386 |
|
400 |
|
408 |
| Minor Sixth... |
|
814 |
|
800 |
|
792 |
| Minor Third... |
|
316 |
|
300 |
|
294 |
| Major Sixth... |
|
884 |
|
900 |
|
906 |
| Semitone... |
|
182 |
|
100 |
|
90 |
Use the buttons to switch this keyboard between equally tempered, pythagorean, and just.
The dissonances occasioned by the upper partial tones are consequently somewhat milder than those due to Pythagorean
intervals, but the combinational tones are much more disagreeable. For the Pythagorean Thirds
These bad combinational tones have always been to me the most annoying part of equally tempered harmonies. When moderately slow passages in Thirds at rather a high pitch are played, they form a horrible bass to them, which is all the more disagreeable for coming tolerably near to the correct bass, and hence sounding as if they were played on some other instrument which was dreadfully out of tune. They are heard most distinctly on the harmonium and violin. Here every professional and even every amateur musician observes them immediately, when their attention is properly directed. And when the ear has once become accustomed to note them, it can even discover them on the piano. In the Pythagorean intonation the combinational tones sound rather as if some one were intentionally playing dissonances. Which of these two evils is the worse, I will not venture to decide. In lower positions where the very low combinational tones can be scarcely, if at all, heard, the equally tempered Thirds have the advantage over the Greek, because they are not so rough, and produce fewer beats. In higher positions the latter advantage is perhaps destroyed by their combinational tones. However, the equally tempered system is capable of effecting everything that can be done by the Pythagorean, and with less expenditure of means.
C. E. Naumann,[7] who has lately defended the Pythagorean as
opposed to the equally tempered system, grounds his reasons chiefly on the fact that the Semitones which separate
the ascending leading tone from the tonic, and the descending minor Seventh from the Third of the chord on which it
has to be resolved, are smaller in the Pythagorean (where they are about \(\tfrac{21}{20}\); as appears in the Table
on p. 313c) than in the equally tempered, where they are about \(\tfrac{18}{17}\);
while they are greatest of all in just intonation, viz. \(\tfrac{16}{15}\). Now in the equally tempered scale there
is only one tone between
Hence the Semitone always approaches the tone on to which it would fall in regular resolution, and the height of the pitch determines the direction of resolution. But although the leading tone plays an important part in modulations, it is perfectly clear that we are not justified in changing its pitch at will in order to bring it nearer to the note on which it has to be resolved. There would otherwise be no limit to our making it come nearer and nearer to that tone, as in the ancient Greek enharmonic mode.[8] Suppose we replace the Pythagorean Semitone, which is about \(\tfrac{4}{5}\) of the natural Semitone, by another still smaller, about \(\tfrac{3}{5}\) of the natural one, say \(\tfrac{16}{15}\times\tfrac{80}{81}\times\tfrac{80}{81}\); the result would be perfectly unnatural as a leading note.[9] We have already seen that the character of the leading note essentially depends upon its being that tone in the scale which is most distantly related to the tonic, and hence most uncertain and alterable [melodically], Hence we are perfectly unjustified in deducing from such a tone the principle of construction for the whole scale.
The principal fault of our present tempered intonation, therefore, does not lie in the Fifths; for their imperfection is really not worth speaking of, and is scarcely perceptible in chords. The fault rather lies in the Thirds, and this error is not due to forming the Thirds by means of a series of imperfect Fifths, but it is the old Pythagorean error of forming the Thirds by means of an ascending series of four Fifths. Perfect Fifths in this case give even a worse result than flat Fifths. The natural relation of the major Third to the tonic, both melodically and harmonically, depends on the ratio \(\tfrac{5}{4}\) of the pitch numbers. Any other Third is only a more or less unsatisfactory substitute for the natural major Third. The only correct system of tones is that in which, as Hauptmann proposed, the system of tones generated by Fifths should be separated from those generated by major Thirds. Now as it is important for the solution of many theoretical questions to be able to make experiments on tones which really form with each other the natural intervals required by theory, to prevent the ear from being deceived by the imperfections of the equal temperament, I have endeavoured to have an instrument constructed by which I could modulate by perfect intervals into all keys.
If we were really obliged to produce in all its completeness the system of tones distinguished by Hauptmann, in order to obtain perfect intervals in all keys, it would certainly be scarcely possible to overcome the difficulties of the problem. Fortunately it is possible to introduce a great and essential simplification by means of the artifice originally invented by the Arabic and Persian musicians, and previously mentioned on p. 281a.
We have already seen that the tones of Hauptmann’s system which are generated by Fifths, and are marked by letters
without any subscribed or superscribed lines, as
Now these two intervals are very nearly alike; \(b_1\) is rather higher than \(c\flat\), but only in the proportion —
or, using the approximation obtained by continued fractions-
The interval between \(c\flat\) and \(b_1\) is consequently about the same as that between a perfect and an equally tempered Fifth.[10]
Now \(b_1\) is the true major Third of \(g\), and if we descend 8 Fifths from \(g\) we arrive at \(c\flat\) thus:
Now, as \(c\flat\) is flatter than \(b_1\), if we diminished[11] all of the Fifths by \(\tfrac{1}{8}\) of the small interval \(\tfrac{886}{885}\) we should arrive at \(b_1\) instead of \(c\flat\).
Now, since the interval \(\tfrac{886}{885}\) is itself on the limits of sensible difference of pitch, the eighth part of this interval cannot be taken into account at all, and we may consequently identify the following tones of Hauptmann's system, by proceeding in a series of Fifth from \(c\flat=b_1\), that is, the upper line with the lower, or -
Among musical instruments, the harmonium, on account of its uniformly sustained sound, the piercing character of its
quality of tone, and its tolerably distinct combinational tones, is particularly sensitive to inaccuracies of
intonation. And as its vibrators also admit of a delicate and durable tuning, it appeared to me peculiarly suitable
for experiments on a more perfect system of tones. I therefore selected an harmonium of the larger kind,[12] with two manuals, and a set of
vibrators for each, and had it so tuned that by using the tones of the two manuals I could play all the major chords
from \(F\flat\) major to \(F\sharp\) major. The tones are thus distributed.

This instrument therefore furnishes 15 major chords and as many minor chords, with perfectly pure Thirds, but with Fifths too flat by \(\tfrac{1}{8}\) of the interval by which an equally tempered Fifth is too flat.[13] On the Lower Manual we have the complete scales of \(C\flat\) major and \(G\) major and in the upper the complete scales of \(E\flat\) major and \(B\) major inclusive complete. All the major scales exist from \(C\flat\) major to \(B\) major, and they can all be played with perfect exactness in the natural intonation. But to modulate beyond \(B\) major on the one side and \(C\flat\) major on the other, it is necessary to make a really enharmonic interchange between \(B_1\) and \(C\flat\), which perceptibly alters the pitch (by a comma \(\tfrac{81}{80}\)).[14] The minor modes on the lower manual are \(B_1\) minor or \(C\flat\) minor complete, on the upper manual \(D_1\sharp\) minor or \(E\flat\) minor.
For the minor keys this series of tones is not quite so satisfactory as for the major keys. The dominant of a minor
key is the Fifth of a minor triad and the root of a major triad. But as the minor chord has to be written as
Of these, the six last tonics from \(C\flat\) to \(B\flat\) are also provided with major scales. Hence there are complete minor scales on all degrees of the scales of \(B_1\) major and \(E_1\) major; and complete minor and major scales on all degrees of the scale of \(B_1\) major, with the exception of \(E_1\).
After previous experiments on another harmonium, where I had at command only the two sets of tones of one octave common to two stops with one manual, I had expected that it would be scarcely observed if either the other minor keys had a somewhat too sharp Pythagorean Seventh, or if minor chords which are themselves rather obscurely harmonious, were executed in Pythagorean intonation. When isolated minor chords are struck the difference is, indeed, not much observed. But when long series of justly-intoned chords have been employed, and the ear has grown accustomed to their effect, it becomes so sensitive to any intermixture of chords in imperfect intonation, that the disturbance is very appreciable.[15]
The least disturbance is caused by taking the Pythagorean Seventh, because this leading tone is in modern compositions scarcely ever used but in the chord of the dominant Seventh, or other dissonances. In a pure major triad its effect is certainly very harsh. But in a discord it has a less disturbing effect, because by its sharpness it brings out the character of the leading note more distinctly. On the other hand, I have found minor chords with Pythagorean Thirds absolutely intolerable when coming between justly-intoned major and minor chords.[15] By allowing, then, a Pythagorean Seventh in the scale, or a Pythagorean major Third in the chord of the dominant Seventh, we may form the following minor scales:[16] —
In the former series, Nos. 8 and 7, we had already \(b\flat\) minor and \(e\flat\) minor, which are a comma sharper than Nos. 13 and 14. Hence the series of minor keys is also completed by the fusion of their extremities through enharmonic interchange.
In most cases it is possible to transpose the music to be played on such instruments, so as to avoid the necessity of making these enharmonic interchanges, provided the modulations do not extend too far into different keys. But if it is not possible to avoid enharmonic interchanges, they must be introduced where two unrelated[17] chords follow each other. This is best done between dissonant chords. Naturally this enharmonic change is always necessary when a piece of music modulates through the whole circle of Fifths — from \(C\) major to \(B\sharp\) major, for example. But Hauptmann is certainly right when he characterises such circular modulation as unnatural artificiality, which could only be rendered possible by the imperfections of our modem system of temperament. Such a process must certainly destroy the hearer’s feeling for the unity of the tonic. For although \(B\sharp\) has very nearly the same pitch as \(C\), or can be even improperly identified with it, the hearer can only restore his feeling for the former tonic by going back on the same path that he advanced. He cannot possibly retain his recollection of the absolute pitch of the first tonic \(C\) after his long modulations up to \(B\sharp\) with such a degree of exactness as to be able to recognise that they are identical. For any fine artistic feeling \(B\sharp\) must remain a tonic far removed from \(C\) on the dominant side; or, more probably, after such distant modulations, the hearer’s whole feeling for tonality will have become confused, and it will then be perfectly indifferent to him in what key the piece ends. Generally speaking, an immoderate use of striking modulations is a suitable and easy instrument in the hands of modern composers, to make their pieces piquant and highly coloured. But a man cannot live upon spice, and the consequence of restless modulation is almost always the obliteration of artistic connection. It must not be forgotten that modulations should be only a means of giving prominence to the tonic by contrasting it with another and then returning into it, or of attaining isolated and peculiar effects of expression.
Since harmoniums with two manuals have usually two sets of vibrators for each manual of which the above system of tuning only uses one, I have had the two others (an 8-foot and a 16-foot stop) tuned in the usual equal temperament, which renders it very easy to compare the effect of this tuning with just intonation, as I have merely to pull out or push in a stop to make the difference.[18]
As regards musical effect, the difference between the just and the equally tempered, or the just and the Pythagorean intonations, is very remarkable. The justly intoned chords, in favourable positions, notwithstanding the rather piercing quality of the tone of the vibrators, possess a full and as it were saturated harmoniousness; they flow on, with a full stream, calm and smooth, without tremor or beat. Equally tempered or Pythagorean chords sound beside them rough, dull, trembling, restless. The difference is so marked that every one, whether he is musically cultivated or not, observes it at once. Chords of the dominant Seventh in just intonation have nearly the same degree of roughness as a common major chord of the same pitch in tempered intonation. The difference between natural and tempered intonation is greatest and most unpleasant in the higher Octaves of the scale, because here the false combinational tones of the tempered intonation are more observable, and the number of beats for equal differences of pitch becomes larger, and hence the roughness greater.
A second circumstance of essential importance is, that the differences of effect between major and minor chords, between different inversions and positions of chords of the same kind, and between consonances and dissonances are much more decided and conspicuous, than in the equal temperament. Hence modulations become much more expressive. Many fine distinctions are sensible, which otherwise almost disappear, as, for instance, those which depend on the different inversions and positions of chords, while, on the other hand, the intensity of the harsher dissonances is much increased by their contrast with perfect chords. The chord of the diminished Seventh, for example, which is so much used in modern music, borders upon the insupportable, when the other chords are tuned justly.[19]
Modern musicians who, with rare exceptions, have never heard any music executed except in equal temperament, mostly make light of the inexactness of tempered intonation. The errors of the Fifths are very small. There is no doubt of that. And it is usual to say that the Thirds are much less perfect consonances than the Fifths, and consequently also less sensitive to errors of intonation. The last assertion is also correct, so long as homophonic music is considered, in which the Thirds occur only as melodic intervals and not in harmonic combinations. In a consonant triad every tone is equally sensitive to false intonation, as theory and experience alike testify, and the bad effect of the tempered triad depends especially on the imperfect Thirds.[20]
There can be no question that the simplicity of tempered intonation is extremely advantageous for instrumental music,
that any other intonation requires an extraordinarily greater complication in the mechanism of the instrument, and
would materially increase the difficulties of manipulation, and that consequently the high development of modern
instrumental music would not have been possible without tempered intonation. But it must not be imagined that the
difference between tempered and just intonation is a mere mathematical subtilty without any practical value. That
this difference is really very striking even to unmusical ears, is shewn immediately by actual experiments with
properly tuned instruments. And that the early musicians, who were still accustomed to the perfect intervals of
vocal music, which was then most carefully practised, felt the same, is immediately seen by a glance at the musical
writings of the latter half of the seventeenth and the earlier part of the eighteenth centuries, at which time there
was much discussion about the introduction of different kinds of temperament, and one new method after another was
invented and rejected for escaping the difficulties, and the most ingenious forms of instrument were designed for
practically executing the enharmonic differences of the tones. Praetorius[21] mentions a universal cymbalum, which he saw at the house of the
court-organist of the Emperor Rudolph II. in Prague, and which had 77 digitals in 4 octaves, or 19 to the octave,
the black digitals being doubled, and others inserted between those for \(e\) and \(f\), and between those for \(b\)
and \(c\).[22] In the older directions for tuning, several tones are usually tuned by Fifths which
beat slightly, and then others as perfect major Thirds. The intervals on which the errors accumulated were called
wolves.
Prætorius
says: 'It is best for the wolf to remain in the
wood with its abominable howling, and not disturb our harmonicas concordantias’. Rameau, too, who at a later
period contributed greatly to the introduction of equal temperament, in 1726[23] still defended a different style of tuning, in which the Thirds
of the more usual keys were kept perfect at the expense of the Fifths and of the unusual keys. Thus he tuned up from
\(C\), in Fifths so much diminished, that the fourth Fifth, instead of being \(E\), became the perfect Third of
\(C\), namely \(E_1 = F\flat\). Then again four Fifths more to \(A_1\flat\), the perfect Third of \(F\flat\),
instead of to \(A\flat\). But then the four Fifths between this \(A_1\flat\) and \(C\) had necessarily[24] to be made too large, because it
is not \(A_1\flat\) but \(A\flat\) which is four perfect Fifths distant from \(C\). This plan of tuning gives the
perfect major Thirds,
The old attempts to introduce more than 12 degrees into the scale have led to nothing practical, because they did not start from any right principle. They always attached themselves to the Greek system of Pythagoras, and imagined only that it was necessary to make a difference between \(c\sharp\) and \(d\flat\), or between \(f\sharp\) and \(g\flat\), and so on. But that is not by any means sufficient, and is not even always correct. According to our system of notation we may identify \(c_1\sharp\) with \(d\flat\), but we must distinguish the \(c\sharp\) found from the relation of Fifths, from the \(c_1\sharp\) found from the relation of Thirds.[28] Hence the attempts to construct instruments with complex arrangements of manuals and digitals, have led to no result, which was at all commensurate with the trouble bestowed upon them, and the increased difficulties of fingering which they occasioned. The only instrument of the kind which is still used is the pedal harp ȧ double mouvement, on which the intonation can be changed by the foot.
Not only habitual use, and the absence of any power to compare its effects with those of just intonation, but some other circumstances are favourable to equal temperament.
First, it should be observed that the disturbances due to beats in the tempered scale, are the less observable the swifter the motion and the shorter the duration of the single notes. When the note is so short that but very few beats can possibly occur while it lasts, the ear has no time to remark their presence. The beats produced by a tempered triad are the following:
1. Beats of the tempered Fifth. Suppose we take the number of vibrations of \(c'\) to be 264, the tempered Fifth
2. Beats of the two first combinational tones of
3. Beats of the major Third
4. Beats of the minor Third
All these beats occur twice as fast when the chord lies an Octave higher, and half as fast when it occurs an Octave lower.
Of these beats, the first, arising from the tempered Fifths, have the least injurious influence on the harmoniousness
of the chord. They are so slow that they can be heard only for very slow notes in the middle parts of the scale, and
then they produce a slow undulation of the chord which may occasionally have a good effect. Beats of the second kind
are most striking for the softer quality of tone. In an Allegro, of four crotchets in a bar, two bars occupy
about three seconds. If, then, the tempered chord
For the same reason the beats of the third and fourth kinds, arising from the Thirds, which are clearly audible on harsher qualities of tone (as on the harmonium), are also decidedly disturbing in the middle positions, even in quick time, and essentially injure the calmness of the triad, because they are twice and thrice as fast as the others. It is only in soft qualities of tone that they are but little observed, or, when observed, are so covered by stronger unbroken tones as to be very slightly marked.
Hence in rapid passages, with a soft quality and moderate intensity of tone, the evils of tempered intonation are but little apparent. Now, almost all instrumental music is designed for rapid movement, and this forms its essential advantage over vocal music. We might, indeed, raise the question whether instrumental music had not rather been forced into rapidity of movement by this very tempered intonation, which did not allow us to feel the full harmoniousness of slow chords to the same extent as is possible from well-trained singers, and that instruments had consequently been forced to renounce this branch of music.
Tempered intonation was first and especially developed on the pianoforte, and hence gradually transferred to other instruments. Now, on the pianoforte circumstances really favour the concealment of the imperfections due to the temperament. The tones of a pianoforte are very loud only at the moment of striking, and their loudness rapidly diminishes. This, as I have already had occasion to mention, causes their combinational tones to be audible at the first moment only, and hence makes them very difficult to hear. Beats from that source must therefore be left out of consideration. The beats which depend on the upper partials have been eliminated in modern pianofortes (especially in the higher Octaves, where they would have done most harm), owing to the mode in which upper partials are greatly weakened and the quality of tone much softened by regulating the striking place, as I have explained in Chap. V. (p. 77b). Hence on a pianoforte the deficiencies of the intonation are less marked than on any instrument with sustained tones, and yet are not quite absent. When I go from my justly-intoned harmonium to a grand pianoforte, every note of the latter sounds false and disturbing, especially when I strike isolated successions of chords. In rapid melodic figures and passages, and in arpeggio chords, the effect is less disagreeable. Hence older musicians especially recommended the equal temperament for the pianoforte alone. Matheson, in doing so, acknowledges that for organs Silberman’s unequal temperament, in which the usual keys were kept pure,[29] is more advantageous. Emanuel Bach says that a correctly tuned pianoforte has the most perfect intonation of all instruments, which in the above sense is correct. The great diffusion and convenience of pianofortes made it subsequently the chief instrument for the study of music and its intonation the pattern for that of all other instruments.
On the other hand, for the harsher stops on the organ, as the mixture and reed stops, the deficiencies of equal temperament are extremely striking. It is considered inevitable that when the mixture stops are played with full chords an awful din (höllenlärm) must ensue, and organists have submitted to their fate. Now this is mainly due to equal temperament, because if the Fifths and Thirds in the pipes for each digital of the mixture stops were not tuned justly, every single note would produce beats by itself. But when the Fifths and Thirds between the notes belonging to the different digitals are tuned in equal temperament, every chord furnishes at once tempered and just Fifths and Thirds, and the result is a restless blurred confusion of sounds. And yet it is precisely on the organ it would be so easy by a few stops to regulate the action for each key so as to produce harmonious chords.[30]
Whoever has heard the difference between justly-intoned and tempered chords, can feel no doubt that it would be the greatest possible gain for a large organ to omit half its stops, which are mostly mere toys, and double the number of tones in the Octave, so as to be able, by means of suitable stops, to play correctly in all keys.[31]
The case is the same for the harmonium as for these stops on the organ. Its powerful false combinational tones and its gritty trembling chords, both due to tempered intonation, are certainly the reason why many musicians pronounce this instrument to be out of tune, and dismiss it at once as too trying to the nerves.
Orchestral instruments can generally alter their pitch slightly. Bowed instruments are perfectly unfettered as to intonation; wind instruments can be made a little sharper or flatter by blowing with more or less force. They are, indeed, all adapted for equal temperament, but good players have the means of indulging the ear to some extent. Hence, passages in Thirds for wind instruments, when executed by indifferent players, often sound desperately false (verzweifelt falsch), whereas good performers, with delicate ears, make them sound perfectly well.
The bowed instruments are peculiar. From the first they have retained their tuning in perfect Fifths. The violins
themselves have the perfect Fifths,
But it is clear that if individual players feel themselves obliged to distinguish the different values of the notes in the different consonances, there is no reason why the bad Thirds of the Pythagorean series of Fifths should be retained in quartett playing. Chords of several parts, executed by several performers in a quartett, often sound very ill, even when each single one of these performers can perform solo pieces very well and pleasantly; and, on the other hand, when quartettes are played by finely-cultivated artists, it is impossible to detect any false consonances. To my mind the only assignable reason for these results is that practised violinists with a delicate sense of harmony, know how to stop the tones they want to hear, and hence do not submit to the rules of an imperfect school. That performers of the highest rank do really play in just intonation, has been directly proved by the very interesting and exact results of Delezenne.[32] This observer determined the individual notes of the major scale, as it was played by distinguished violinists and violoncellists, by means of an accurately gauged string, and found that these players produced correctly perfect Thirds and Sixths, and neither equally tempered nor Pythagorean Thirds or Sixths. I was fortunate enough to have an opportunity of making similar observations by means of my harmonium on Herr Joachim. He tuned his violin exactly with the \(g±d±a±e\) of my instrument. I then requested him to play the scale, and immediately he had played the Third or Sixth, I gave the corresponding note on the harmonium. By means of beats it was easy to determine that this distinguished musician used \(b_1\) and not \(b\) as the major Third to \(g\), and \(e_1\) not \(e\) as the Sixth.[33] But if the best players who are thoroughly acquainted with what they are playing are able to overcome the defects of their school and of the tempered system, it would certainly wonderfully smooth the path of performers of the second order, in their attempts to attain a perfect ensemble, if they had been accustomed from the first to play the scales by natural intervals. The greater trouble attending the first attempts would be amply repaid by the result when the ear has once become accustomed to hear perfect consonances. It is really much easier to apprehend the differences between notes of the same name in just intonation than people usually imagine, when the ear has once become accustomed to the effect of just consonances. A confusion between \(a_1\) and \(a\) in a consonant chord on my harmonium strikes me with the same readiness and certainty as a confusion between \(A\) and \(A\flat\) on a pianoforte.[34]
I am, however, too little acquainted with the technicalities of violin-playing, to attempt making any proposals for a definite regulation of the tonal system of bowed instruments. This must be left to masters of this instrument who at the same time possess the powers of a composer. Such men will readily convince themselves by the testimony of their ears, that the facts here adduced are correct, and perceive that, far from being useless mathematical speculations, they are practical questions of very great importance.
The case is precisely similar for our present singers. For singing, intonation is perfectly free, whereas on bowed instruments, the five tones of the open strings at least have an unalterable pitch. In singing the pitch can be made most easily and perfectly to follow the wishes of a fine musical ear. Hence all music began with singing;[35] and singing will always remain the true and natural school of all music. The only intervals which singers can strike with certainty and perfection, are such as they can comprehend with certainty and perfection, and what the singer easily and naturally sings the hearer will also easily and naturally understand.[36]
Down to the seventeenth century singers were practised by the monochord, for which Zarlino in the middle of the sixteenth century reintroduced the correct natural intonation. Singers were then practised with a degree of care of which we have at present no conception. We can even now see from the Italian music of the fifteenth and sixteenth centuries that they were calculated for most perfect intonation of the chords, and that their whole effect is destroyed as soon as this intonation is executed with insufficient precision.
But it is impossible not to acknowledge that at the present day few even of our opera singers are able to execute a little piece for several voices, when either totally unaccompanied, or at most accompanied by occasional chords (as, for example, the trio for the three masks, Protegga il giusto cielo, from the finale to the first act of Mozart’s Don Giovanni), in a manner suited to give the hearer a full enjoyment of its perfect harmony. The chords almost always sound a little sharp or uncertain, so that they disturb a musical hearer. But where are our singers to learn just intonation and make their ears sensitive for perfect chords? They are from the first taught to sing to the equally-tempered pianoforte. If a major chord is struck as an accompaniment, they may sing a perfect consonance with its root, its Fifth, or its Third. This gives them about the fifth part of a Semitone for their voices to choose from without decidedly singing out of harmony, and even if they sing a little sharper than consonance with the sharp Third requires, or a little flatter than consonance with the flat Fifth requires, the harmoniousness of the chord will not be really much more damaged. The singer who practises to a tempered instrument has no principle at all for exactly and certainly determining the pitch of his voice.[37]
On the other hand, we often hear four musical amateurs who have practised much together, singing quartettes in perfectly just intonation. Indeed, my own experience leads me almost to affirm that quartetts are more frequently heard with just intonation when sung by young men who scarcely sing anything else, and often and regularly practise them, than when sung by instructed solo singers who are accustomed to the accompaniment of the pianoforte or the orchestra. But correct intonation in singing is so far above all others the first condition of beauty, that a song when sung in correct intonation even by a weak and unpractised voice, always sounds agreeable, whereas the richest and most practised voice offends the hearer when it sings false, or sharpens.
The case is the same as for bowed instruments. The instruction of our present singers by means of tempered instruments is unsatisfactory, but those who possess good musical talents are ultimately able by their own practice to strike out the right path for themselves, and overcome the error of their original instruction. They even succeed the earlier, perhaps, the sooner they quit school, although, of course, I do not mean to deny that fluency in singing, and the disuse of all kinds of bad ways can only be acquired in school.
It is clearly not necessary to temper the instruments to which the singer practises. A single key suffices for these exercises, and that can be correctly tuned. We do not require to use the same piano for the teaching to sing and for playing sonatas. Of course it would be better to practise the singer to a justly-intoned organ or harmonium in which by means of two manuals all keys may be used.[38] Sustained tones are preferable as an accompaniment because the singer himself can immediately hear the beats between the instrument and his voice when he alters the pitch slightly. Draw his attention to these beats, and he will then have a means of checking his own voice in the most decisive manner. This is very easy on my justly-intoned harmonium, as I know by experience. It is only after the singer has learned to hear every slight deviation from correctness announced by a striking incident, that it becomes possible for him to regulate the motions of his larynx and the tension of his vocal chords with sufficient delicacy to produce the tone which his ear demands. When we require a delicate use of the muscles of any part of the human body, as, in this case, of the larynx, there must be some sure means of ascertaining whether success has been attained. Now the presence or absence of beats gives such a means of detecting success or failure when a voice is accompanied by sustained chords in just intonation. But tempered chords which produce beats of their own are necessarily quite unsuited for such a purpose.
Finally, we cannot, I think, fail to recognise the influence of tempered intonation upon the style of composition. The first effect of this influence was favourable. It allowed composers as well as players to move freely and easily into all keys, and thus opened up a new wealth of modulation. On the other hand, we likewise cannot fail to recognise that the alteration of intonation also compelled composers to have recourse to some such wealth of modulation. For when the intonation of consonant chords ceased to be perfect, and the differences between their various inversions and positions were, as a consequence, nearly obliterated, it was necessary to use more powerful means, to have recourse to a frequent employment of harsh dissonances, and to endeavour by less usual modulations to replace the characteristic expression, which the harmonies proper to the key itself had ceased to possess. Hence in many modern compositions dissonant chords of the dominant Seventh form the majority, and consonant chords the minority, yet no one can doubt that this is the reverse of what ought to be the case; and continual bold modulational leaps threaten entirely to destroy the feeling for tonality. These are unpleasant symptoms for the further development of art. The mechanism of instruments and attention to their convenience, threaten to lord it over the natural requirements of the ear, and to destroy once more the principle upon which modern musical art is founded, the steady predominance of the tonic tone and tonic chord. Among our great composers, Mozart and Beethoven were yet at the commencement of the reign of equal temperament. Mozart had still an opportunity of making extensive studies in the composition of song. He is master of the sweetest possible harmoniousness, where he desires it, but he is almost the last of such masters. Beethoven eagerly and boldly seized the wealth offered by instrumental music, and in his powerful hands it became the appropriate and ready tool for producing effects which none had hitherto attempted. But he used the human voice as a mere handmaid, and consequently she has also not lavished on him the highest magic of her beauty.
And after all, I do not know that it was so necessary to sacrifice correctness of intonation to the convenience of musical instruments. As soon as violinists have resolved to play every scale in just intonation, which can scarcely occasion any difficulty, the other orchestral instruments will have to suit themselves to the correcter intonation of the violins. Horns and trumpets have already naturally just intonation.[39]
Moreover, we must observe that when just intonation is made the groundwork of modulations, even comparatively simple modulational excursions will occasion enharmonic confusions (amounting to a comma) which do not appear as such in the tempered system.[40]
To me it seems necessary that the new tonic into which we modulate should be related to the tonic in which we are playing; the nearer the relationship, the more striking the transition. Again, it is not advisable to remain long in a key which is not related to the principal tonic of the piece. With these principles the rules for modulation usually given coincide. The easiest and most usual transitions are into the key of the dominant or subdominant, these tones being, as is well known, the nearest relations of the first tonic. Hence if the original key is \(C\), we can pass immediately into \(G\) major, and thus change the tones \(F\) and \(A_1\) of the scale of \(C\) major into \(F_1\sharp\) and \(A\). Or we can pass into \(F\) major by exchanging \(B_1\) and \(D\) for \(B\flat\) and \(D_1\). After this step has been made, the music will often pass into a key with a tonic related to \(C\) in the second degree only, as from \(G\) to \(D\) or from \(F\) to \(B\flat\). By proceeding in this way we should come to keys as \(A\) and \(E\flat\), of which the relation to the original tonic \(C\) would be very obscure and in which it would certainly not be advisable to remain long for fear of too much weakening the feeling for the original tonic.
Again, we may also modulate from the principal tonic \(C\) to its Thirds and Sixths, to \(E_1\) and \(A_1\) or \(E^1\flat\) and \(A^1\flat\). In tempered intonation these changes seem to be the same as from \(G\) and \(D\) to \(A\) and \(E\), or from \(F\) and \(B\flat\) to \(E\flat\) and \(A\flat\). But they differ in the pitch, as shewn by the different marks \(A\) and \(A_1\), &c. In the tempered intonation it seems allowable to go by a Sixth from \(c\) to the key \(a\), and then by Fifths back to \(d\), \(g\), and then \(c\) again. But in reality we thus reach a different \(c\) from that with which we began. By such a transition, which is certainly not quite natural, we should be obliged to make an enharmonic exchange [alteration of pitch by a comma], and this would be best done while in the key of \(d\), since both \(d\) and \(d_1\) are related to \(c\) in the second degree. In the complicated modulations of modem composers such enharmonic changes will of course have to be often made. A cultivated taste will have to judge in each individual case how they are to be introduced, but it will be probably advisable to retain the rules already mentioned, and to choose the intonation of the new tonics introduced by modulation in such a manner as will keep them as closely related to the principal tonic as possible. Enharmonic changes are least observed when they are made immediately before or after strongly dissonant chords, as those of the diminished Seventh. Such enharmonic changes of pitch are already sometimes clearly and intentionally made by violinists, and where they are suitable even produce a very good effect.[41]
[42]If we desire to produce a scale in almost precisely just intonation, which will allow of an indefinite power of modulation without having recourse to enharmonic changes,[43] we can effect our purpose by the division of the Octave into 53 exactly equal parts, as was long ago proposed by Mercator [to represent Pythagorean intonation]. Mr. R H. M. Bosanquet[44] has recently provided this temperament as realised on an harmonium, with a symmetrically arranged fingerboard. When the Octave is divided into 53 equal intervals or degrees, 31 such degrees give an almost perfect Fifth, the error of which is only \(\tfrac{1}{28}\) of the error of the Fifth of the usual equal temperament, and 17 of these degrees give a major Third, of which the error in defect is only \(\tfrac{5}{7}\) of the above-named error of the Fifth in equal temperament.[45] The error of the Fifth in this system must be considered as quite inappreciable, that of the major Third is still more difficult to perceive than that of the equally tempered Fifth.[46] In these degrees the major scale will be
| \(C\) | \(D\) | \(E_1\) | \(F\) | \(G\) | \(A_1\) | \(B_1\) | \(C\) | ||||||||
| degrees | 0 | 9 | 17 | 22 | 31 | 39 | 48 | 53 | |||||||
| differences | 9 | 8 | 5 | 9 | 8 | 9 | 5 |
These differences of 9, 8, 5 correspond to the major, minor, and half Tone of the just scale. Each separate degree of the scale corresponds nearly with the interval 77 : 76 [= 22.6 cents] and is therefore extremely little greater than the comma 81 : 80 [= 21.5 cents], which in the just scale gives the difference between a large or diatonic Semitone [16 : 15 = 112 cents] and a small Semitone or limma [256 : 243 = 90 cents]. The ear cannot distinguish this scale from the just,[47] and in its practical applications it admits of unlimited modulation in what is equal to exact intonation. The difference between our \(c_1\) and \(c\), or our \(c\) and \(c^1\) would answer to sharpening by one degree. Mr. Bosanquet therefore employs the convenient signs \(\setminus c\) for \(c_1\), and \(/ c\) for \(c^1\), \(\setminus \setminus c\) for \(c_2\), &c. These signs, \ and /, he also employs before notes on the staff, exactly as we employ \(\sharp\) and \(\flat\). The fingerboard is arranged in a very comprehensible and symmetrical way to make the fingering of all scales and all chords the same in all keys.[48] A diagram of the keyboard will be found in App. XIX. [49]
Perhaps a justification is needed for our having in this whole theory of keys and modulations, identified the key of the Octave with that of its root, while we have distinguished the key of the Twelfth. In the usual school of musical theory, the meaning of the sound of the Octave is completely identified with that of its root, and is so treated. For us, on the other hand, the Octave is only the Tone most nearly and clearly related to the root, but its relationship is the same in kind as that of the Twelfth, or the next higher major Third (Seventeenth) to the root.
Now we have shewn in p. 273a that in the particular relation of the formation of scales, that is of the determination of the key, the higher Octave introduces the same series of directly related tones as does the lower, although in a somewhat different order of strength of relationship. Only throughout the formation of the lower Octave the tones of the major scale are favoured, and in the formation of the upper Octave those of the minor scale are preferred, but not to the exclusion of those of other scales.
When we proceed beyond the limits of the first Octave, the relationships of tone depending on the six first partials give only the Tenth and Twelfth. The other steps of the scales have then to be filled up with tones related in the second degree, and, among these, the relations of the Octave must have the preference, and next those of the Twelfth. Hence in the second Octave we have necessarily a repetition of the scale of the first. By this means, in the formation of scales an equivalence of Octaves is established, without any necessity for assuming a specifically different relation of similarity between them and the root, as we had to do for the other consonances. In the formation of consonant intervals, the usual theory of music also considers the Octaves as equivalent to the roots. This is within certain limits correct, because the intervals usually considered as consonant remain consonant when one of their tones is transposed by an Octave, or at least produce intervals which lie on the limits of consonance. But here the usual rule of the school really gave a very imperfect expression of the facts, since, as we have shewn in Chapters X., XI., and XII., the degree and sequence of the consonance are really materially altered by these changes, and composers who have outgrown the rules of the school, have also very clearly had regard to these alterations.
| meaning of our notation: | |
| F fa ut | f |
| tonus |
204 cents = Tone |
| G sol re ut | g |
| tonus | 204 cents = Tone |
| a la mi re | a |
| semitonium | 90 cents = Semitone |
| b fa | \(b\flat\) |
| apothome | 114 cents = Apotome |
| B mi Trittonus | b Tritone 612 cents |
| semitone | 90 cents = Semitone |
| c sol fa ut | c' Fifth 702 cents |
| Notes | Just, Difference | Pythagorean, Difference | Tempered, Difference | |||
| \(c'\) | 264 | 264 | 264 | |||
| 66=C | 70.12 | 68.61 | ||||
| \(e'\) | 330 | 334.12 | 332.61 | |||
| 65=C | 61.88=\(B_/\) | 62.94 | ||||
| \(g'\) | 396 | 396 | 395.55 | |||
| 99=G | 105.19 | 102.81 | ||||
| \(b'\) | 495 | 501.19 | 498.36 | |||
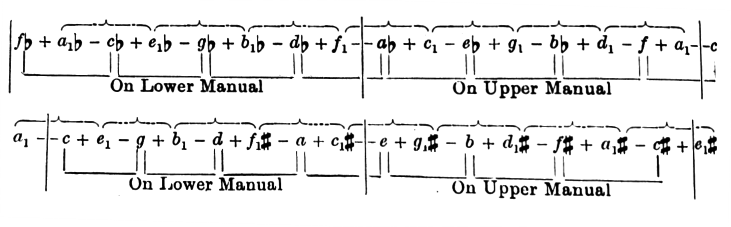
The tuning of this instrument was easily managed. Herr Schiedmayor succeeded at the first attempt by the following direction. Starting from \(a\) on the lower manual, tune the Fifths \(d \pm a\), \(g \pm d\), \(c±g\) perfectly just, and thus obtain \(c, g,d\). Then tune the major chords \(c+e_1-g\), \(g+b_1-d\), \(d+f_1\sharp-a\), giving the three tones \(e_1 b_1 f_1\sharp\) and finally the Fifth, \(f_1\sharp \pm c_1\sharp\), to obtain \(c_1\sharp\). Then putting \(e_1=f\flat\), \(b_1=c\flat\), \(f_1\sharp=g\flat\), \(c_1\sharp=d\flat\), tune the major chords \(f\flat+a_1\flat-c\flat\), \(c\flat+e_1\flat-g\flat\), \(g\flat+b_1\flat-d\flat\) with pure Thirds giving no beats, thus obtaining \(a_1\flat , e_1\flat , b_1\flat\), and finally the Fifth \(b_1\flat \pm f_1\) giving \(f_1\). This completes the tuning of the notes on the lower manual. For the upper manual first tune \(e\) as the perfect Fifth of the \(a\) in the lower manual, and then the three major chords \(e+g_1\sharp-b\), \(b+d_1\sharp-f\sharp\), \(f\sharp+a_1\sharp-c\sharp\), and the Fifth \(a_1\sharp \pm e_1\sharp\), giving \(b, \space f\sharp, \space c\sharp\), and then \(G_1\sharp\), \(d_1\sharp\), \(a_1\sharp\) and also \(e_1\sharp\). Then put \(g_1\sharp = a\flat\), \(d_1\sharp = e\flat\), \(a_1\sharp = b\flat\), \(e_1\sharp = f\), and tune the Thirds in the major chords \(a\flat+c_1-e\flat\), \(e\flat+g_1-b\flat\), \(b\flat+d_1-f\), and the Fifth \(d_1 \pm a_1\). this gives \(c_1\), \(g_1\), \(d_1\), and \(a_1\), and completes the whole tuning, which is much easier than for a series of equally tempered tones.
| I | II | III | IV | V | VI | ||||||
| \(C\sharp\) | 114 | \(E_1\sharp\) | 500 | \(g_2\sharp\sharp\) | 886 | \(d^1\flat\) | 112 | \(f\) | 498 | \(A_1\) | 884 |
| \(F\sharp\) | 612 | \(A_1\sharp\) | 998 | \(c_2\sharp\sharp\) | 184 | \(g^1\flat\) | 610 | \(b\flat\) | 996 | \(D_1\) | 182 |
| \(B\) | 1110 | \(D_1\sharp\) | 296 | \(f_2\sharp\sharp\) | 682 | \(c^1\flat\) | 1108 | \(e\flat\) | 294 | \(G_1\) | 680 |
| \(E\) | 408 | \(G_1\sharp\) | 794 | \(b_2\sharp\sharp\) | 1180 | \(f^1\flat\) | 406 | \(a\flat\) | 792 | \(C_1\) | 1178 |
| \(A\) | 906 | \(C_1\sharp\) | 92 | \(e_2\sharp\) | 478 | \(b^1\flat\flat\) | 904 | \(d\flat\) | 90 | \(F_1\) | 476 |
| \(D\) | 204 | \(F_1\sharp\) | 590 | \(a_2\sharp\) | 976 | \(e^1\flat\flat\) | 202 | \(g\flat\) | 588 | \(B_1\flat\) | 974 |
| \(G\) | 702 | \(B_1\) | 1088 | \(d_2\sharp\) | 274 | \(a^1\flat\flat\) | 700 | \(c\flat\) | 1086 | \(E_1\flat\) | 272 |
| \(C\) | 0 | \(E_1\) | 386 | \(g_2\sharp\) | 772 | \(d^1\flat\flat\) | 1198 | \(f\flat\) | 384 | \(A_1\flat\) | 770 |
[The theoretical flattening of all the Fifths by \(\tfrac{1}{8}\) of a skhisma is here neglected, as it would be impossible by ear only, and in all probability many other errors in tuning were committed, which could not be detected. The result is that the two manuals were tuned to the following tones, using capital letters to represent the large or white digitals, and the small letters the small or black digitals. The Roman letters below shew the secondary meaning attached to the letters above them for the tuning of the notes marked with a • above them.
$$ \begin{gathered} \text{Upper Manual}\\ \text{\.{C}}_1 \quad \text{c}\sharp \quad \text{\.{D}}_1 \quad \text{d}_1\sharp \quad \text{E} \quad \text{E}_1\sharp \quad \text{f}\sharp \quad \text{\.{G}}_1 \quad \text{g}_1\sharp \quad \text{\.{A}}_1 \quad \text{a}_1\sharp \quad \text{B} \\ \hspace{15mm} \text{e}\flat \hspace{12mm} \text{f} \hspace{20mm} \text{a}\flat \hspace{13mm} \text{b}\flat \end{gathered} $$ $$ \begin{gathered} \text{Lower Manual}\\ \text{C} \quad \text{c}_1\sharp \quad \text{D} \quad \text{\.{e}}_1\flat \quad \text{E}_1 \quad \text{F}_1\sharp \quad \text{f}_1\sharp \quad \text{G} \quad \text{\.{a}}_1\flat \quad \text{A} \quad \text{\.{b}}_1\flat \quad \text{B}_1 \\ \hspace{7mm} \text{d}\flat \hspace{18mm} \text{F}\flat \hspace{12mm} \text{g}\flat \hspace{33mm} \text{C}\flat \end{gathered} $$
To make it more clear how the 24 notes of this instrument represent 48 by neglecting the skhisma, I have below arranged the scale on the duodenary system (major Thirds in lines, Fifths in columns, App. XX. sect. E. art. 18), and given the proper number of cents for each note, using capitals for the notes actually tuned, and small letters for those obtained by substitution. The notes above the horizontal lines were in the upper manual, those below it on the lower.
It is thus seen l) that the notes in cols. I., II., III. are exactly 2 cents sharper than those in cols. IV., V., VI. 2) that only cols. I., II., VI. were tuned, and that IV., V., and III. without being tuned were assumed to be identical with them respectively. 3) That cols. I. II., III. form a series of Fifths down or Fourths up, of which only two, namely \(C\) to \(E\sharp\) and \(E_1\), to \(g_2\sharp\sharp\), are defective, being both 700 cents down or 500 up, in place of 702 and 498 as all the others. 4) That the simplest way of tuning would be to take \(A\) to pitch, and then \(A+C_1\sharp\), and \(C_1\sharp+e_2\sharp\) as perfect major Thirds, and then from \(A,\space C_1\sharp, \space e_2\sharp\) to tune the rest of the notes in their columns by perfect Fifths and Fourths, naming the notes in col. III. for convenience as those in col. VI. Afterwards the identity of the first three with the last three columns would be assumed. All the properties and defects of this system of tuning can be immediately deduced from the above diagram.— Translator.] ↵
On converting the ratio of the extent of the interval of a Fifth to that of an Octave (that is log. 1-5: log. 2) into a continued fraction, we get the following approximations :
| 12 | 53 | 306 Fifths |
| nearly=7 | 31 | 179 Octaves |
And by a similar approximation
| 3 | 28 | 59 major Thirds |
| nearly=1 | 9 | 19 Octaves |
[As these approximations give no conception of the extreme closeness with which the 53 division, if accurately tuned, would approximate to just intonation, I annex the following table:
| Note | Just cents | 53 division cents | No. of degrees | ||
| \(C\) |
|
|
0 | ||
| \(C^1\) |
|
|
1 | ||
| \(D_1\) |
|
|
8 | ||
| \(D\) |
|
|
9 | ||
| \(E^1\flat\) |
|
|
14 | ||
| \(E\) |
|
|
17 | ||
| \(^7F\) |
|
|
21 | ||
| \(F\) |
|
|
22 | ||
| \(G\) |
|
|
31 | ||
| \(A^1\flat\) |
|
|
36 | ||
| \(A_1\) |
|
|
39 | ||
| \(^7B\flat\) |
|
|
43 | ||
| \(B\flat\) |
|
|
996.091 | 996.226 | 44 |
| \(B^1\flat\) |
|
|
45 | ||
| \(B_1\) |
|
|
48 | ||
| \(C\) |
|
|
53 | ||
| \(^{17}D\flat\) |
|
|
58 |
Hence for all tertian intervals the approximation is within 2 cents, often within 1 cent. The septimal comma being greater than 1 degree, the \(^7B\flat\) is too sharp by 6 cents. Still the 58 div. chord \(C : E_1 : G : ^7B\flat\) is a great improvement on the just \(C : E_1: G : B\flat\). The 17th harmonic is 8 cents too sharp, but the chord of the diminished Seventh in the 53 div. \(E_1 : G : ^7B\flat : ^{17}D\flat\) is much superior to the just form \(E_1 : G : B\flat : D^1\flat\), though from its just surroundings inferior in effect to the equally tempered \(E:G:B\flat:D\flat\).— Translator.]
↵