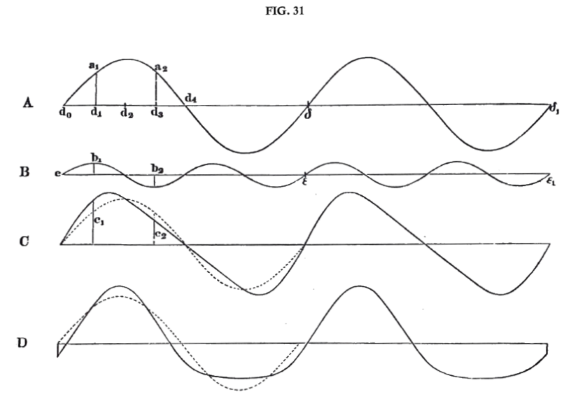
Up to this point we have not endeavoured to analyse given musical tones further than to determine the differences in the number and loudness of their partial tones. Before we can determine the function of the ear in apprehending qualities of tone, we must inquire whether a determinate relative strength of the upper partials suffices to give us the impression of a determinate musical quality of tone or whether there are not also other perceptible differences in quality which are independent of such a relation. Since we deal only with musical tones, that is, with such as are produced by exactly periodic motions of the air, and exclude all irregular motions of the air which appear as noises, we can give this question a more definite form. If we suppose the motion of the air corresponding to the given musical tone to be resolved into a sum of pendular vibrations of air, such individual pendular vibrations will not only differ from each other in force or amplitude for different forms of the compound motion, but also in their relative position, or, according to physical terminology, in their difference of phase. For example, if we superimpose the two pendular vibrational curves A and B, fig. 31 (p. 120), first with the point e of b on the point d0 of a, and next with the point e of b on the point d1 of a, we obtain the two entirely distinct vibrational curves C and D. By further displacement of the initial point e so as to place it on d2 or d3 we obtain other forms, which are the inversions of the forms C and D, as has been already shewn (supra, p. 32). If, then, musical quality of tone depends solely on the relative force of the partial tones, all the various motions C, D, &c., must make the same impression on the ear. But if the relative position of the two waves, that is the difference of phase, produces any effect, they must make different impressions on the ear.

Now to determine this point it was necessary to compound various musical tones out of simple tones artificially, and to see whether an alteration of quality ensued when force was constant but phase varied. Simple tones of great purity, which can have both their force and phase exactly regulated, are best obtained from tuning-forks having the lowest proper tone reinforced, as has been already described (p. 54), by a resonance chamber, and communicated to the air. To set the tuning-forks in very uniform motion, they were placed between the limbs of a little electro-magnet, as shewn in fig. 32, opposite. Each tuning-fork was screwed into a separate board d d, which rested upon pieces of india-rubber tubing e e that were cemented below it, to prevent the vibrations of the fork from being directly communicated to the table and hence becoming audible. The limbs b b of the electro-magnet are surrounded with wire, and its pole f is directed to the fork. There are two clamp screws g on the board d d which are in conductive connection with the coils of the electro-magnet, and serve to introduce other wires which conduct the electric current. To set the forks in strong vibration the strength of these streams must alternate periodically. These are generated by a separate apparatus to be presently described (fig. 33, p. 122).
When forks thus arranged are set in vibration, very little indeed of their tone is heard, because they have so little means of communicating their vibrations to the surrounding air or adjacent solids. To make the tone strongly audible, the resonance chamber i, which has been previously tuned to the pitch of the fork, must be brought near it. This resonance chamber is fastened to another board k, which slides in a proper groove made in the board d d, and thus allows its opening to be brought very near to the fork. In the figure the resonance chamber is shewn at a distance from the fork in order to exhibit the separate parts distinctly; when in use, it is brought as close as possible to the fork. The mouth of the resonance chamber can be closed by a lid l attached to a lever m. By pulling the string n the lid is withdrawn from the opening and the tone of the fork is communicated to the air with great force. When the thread is let loose, the lid is brought over the mouth of the chamber by the spring p, and the tone of the fork is no longer heard. By partial opening of the mouth of the chamber, the tone of the fork can be made to receive any desired intermediate degree of strength. The whole of the strings which open the various resonance chambers belonging to a series of such forks are attached to a keyboard in such a way that by pressing a key the corresponding chamber is opened.
Sing a vowel and then play a synthesized version back
Number of Harmonics displayed:
At first I had eight forks of this kind, giving the tones
To set the forks in motion, intermittent electrical currents had to be conducted through the coils of the electro-magnet, giving as many electrical shocks as the lowest forks made vibrations in a second, namely 120. Every shock makes the iron of the electro-magnet b b momentarily magnetic, and hence enables it to attract the prongs of the fork, which are themselves rendered permanently magnetic. The prongs of the lowest fork \(B\flat\) are thus attracted by the poles of the electro-magnet, for a very short time, once in every vibration; the prongs of the second for \(b\flat\), which moves twice as fast, once every second vibration, and so on. The vibrations of the forks are therefore both excited and kept up as long as the electric currents pass through the apparatus. The vibrations of the lower forks are very powerful, those of the higher proportionally weaker.

The apparatus shewn in fig. 33 (p. 122) serves to produce intermittent currents of exactly determinate periodicity. A tuning-fork a is fixed horizontally between the limbs b b of an electro-magnet; at its extremities are fastened two platinum wires c c, which dip into two little cups d filled half with mercury and half with alcohol, forming the upper extremities of brass columns. These columns have clamping screws i to receive the wires, and stand on two boards f, g, which turn about an axis, as at f, and which can each be somewhat raised or lowered by a thumb screw, as at g, so as to make the points of the platinum wires c c exactly touch the mercury below the alcohol in the cups d. A third clamping screw e is in conductive connection with the handle of the tuning-fork. When the fork vibrates, and an electric current passes through it from i to e, the current will be broken every time that the end of the fork a rises above the surface of the mercury in the cup d, and re-made every time the platinum wire dips again into the mercury. This intermittent current being at the same time conducted through the electromagnet b b, fig. 33, the latter becomes magnetic every time it passes, and thus keeps up the vibrations of the fork a, which is itself magnetic. Generally only one of the cups d is used for conducting the current. Alcohol is poured over the mercury to prevent the latter from being burned by the electrical sparks which arise when the stream is interrupted. This method of interrupting the current was invented by Neef, who used a simple vibrating spring in place of the tuning-fork, as may be generally seen in the induction apparatus so much used for medical purposes. But the vibrations of a spring communicate themselves to all adjacent bodies and are for our purposes both too audible and too irregular. Hence the necessity of substituting a tuning-fork for the spring. The handle of a well worked symmetrical tuning-fork is extremely little agitated by the vibrations of the fork and hence does not itself agitate the bodies connected with it, so powerfully as the fixed end of a straight spring. The tuning-fork of the apparatus in fig. 33 must be in exact unison with the prime tone \(B\flat\). To effect this I employ a little clamp of thick steel wire h, placed on one of the prongs. By slipping this towards the free end of the prong the tone is deepened, and by slipping it towards the handle of the fork, the tone is raised.[2]

When the whole apparatus is in action, but the resonance chambers are closed, all the forks are maintained in a state of uniform motion, but no sound is heard, beyond a gentle humming caused by the direct action of the forks on the air. But on opening one or more resonance chambers, the corresponding tones are heard with sufficient loudness, and are louder as the lid is more widely opened. By this means it is possible to form, in rapid succession, different combinations of the prime tone with one or more harmonic upper partials having different degrees of loudness, and thus produce tones of different qualities.
Among the natural musical tones which appear suitable for imitation with forks, the vowels of the human voice hold the first rank, because they are accompanied by comparatively little extraneous noise and shew distinct differences of quality which are easy to seize. Most vowels also are characterised by comparatively low upper partials, which can be reached by our forks; E and I alone somewhat exceed these limits. The motion of the very high forks is too weak for this purpose when influenced only by such electrical currents as I was able to use without disturbance from the noise of the electric sparks.
The first series of experiments was made with the eight forks \(B\flat\) to \(b''\flat\). With these U, O, Ö, and even A could be imitated; the last not very well because of my not possessing the upper partials \(c'''\) and \(d'''\), which lie immediately above its characteristic tone \(b''\flat\), and are sensibly reinforced in the natural sound of this vowel. The prime tone \(B\flat\) of this series, when sounded alone, gave a very dull U, much duller than could be produced in speech. The sound became more like U when the second and third partial tones \(b\flat\) and \(f'\) were allowed to sound feebly at the same time. A very fine O was produced by taking \(b'\flat\) strong, and \(b\flat\), \(f'\), \(d''\) more feebly; the prime tone \(B\flat\) had then, however, to be somewhat damped. On suddenly changing the pressure on the keys and hence the position of the lids before the resonance chambers, so as to give \(B\flat\) strong, and all the upper partials weak, the apparatus uttered a good clear U after the O.
A or rather A° [nearly o in not] was produced by making the fifth to the eighth partial tones as loud as possible, and keeping the rest under.
The vowels of the second and third series, which have higher characteristic tones, could be only imperfectly imitated by bringing out their reinforced tones of the lower pitch. Though not very clear in themselves they became so by contrast on alternation with U and O. Thus a passably clear Ä was obtained by giving loudness chiefly to the fourth and fifth tones, and keeping down the lower ones, and a sort of E by reinforcing the third, and letting the rest sound feebly. The difference between O and these two vowels lay principally in keeping the prime tone \(B\flat\) and its Octave \(b\flat\) much weaker for Ä and E than for O.[3]
To extend my experiments to the brighter vowels, I afterwards added the forks \(d'''\), \(f''\), \(a'''\flat\), \(b'''\flat\), the two upper ones of which, however, gave a very faint tone, and I chose \(b\flat\) as the prime tone in place of \(B\flat\). With these I got a very good Ä and A, and at least a much more distinct E than before. But I could not get up to the high characteristic tone of I.
In this higher series of forks, the prime tone \(b\flat\), when sounded alone, reproduced U. The same prime \(b\flat\), with moderate force, accompanied with a strong Octave \(b'\flat\), and a weaker Twelfth \(f''\), gave O, which has the characteristic tone \(b'\flat\). A was obtained by taking \(b\flat\), \(b'\flat\), and \(f''\) moderately strong, and the characteristic tones \(b''\flat\) and \(d'''\) very strong. To change A into Ä it was necessary to increase somewhat the force of \(b'\flat\) and \(f''\) which were adjacent to the characteristic tone \(d''\), to damp \(b''\flat\), and bring out \(d'''\) and \(f'''\) as strongly as possible. For E the two deepest tones of the series, \(b\flat\) and \(b'\flat\), had to be kept moderately loud, as being adjacent to the deeper characteristic tone \(f'\), while the highest \(f'''\), \(a'''\flat\), \(b'''\flat\) had to be made as prominent as possible. But I have hitherto not succeeded so well with this as with the other vowels, because the high forks were too weak, and because perhaps the upper partials which lie above the characteristic tone \(b'''\flat\) could not be entirely dispensed with.[4]
Here, you can see how different vowel sounds produce different frequency and different harmonics.
In precisely the same way as the vowels of the human voice, it is possible to imitate the quality of tone produced by organ pipes of different stops, if they have not secondary tones which are too high, but of course the whizzing noise, formed by breaking the stream of air at the lip, is wanting in these imitations. The tuning-forks are necessarily limited to the imitation of the purely musical part of the tone. The piercing high upper partials, required for imitating reed instruments, were absent, but the nasality of the clarinet was given by using a series of unevenly numbered partials, and the softer tones of the horn by the full chorus of all the forks.
But though it was not possible to imitate every kind of quality of tone by the present apparatus, it sufficed to decide the important question as to the effect of altered difference of phase upon quality of tone. As I particularly observed at the beginning of this chapter, this question is of fundamental importance for the theory of auditory sensation. The reader who is unused to physical investigations must excuse some apparently difficult and dry details in the explanation of the experiments necessary for its decision.
The simple means of altering the phases of the secondary tones consists in bringing the resonance chambers somewhat out of tune by narrowing their apertures, which weakens the resonance, and at the same time alters the phase. If the resonance chamber is tuned so that the simple tone which excites its strongest resonance coincides with the simple tone of the corresponding fork, then, as the mathematical theory shews,[5] the greatest velocity of the air at the mouth of the chamber in an outward direction, coincides with the greatest velocity of the ends of the fork in a inward direction. On the other hand, if the chamber is tuned to be slightly deeper than the fork, the greatest velocity of the air slightly precedes, and if it is tuned slightly higher, that greatest velocity slightly lags behind the greatest velocity of the fork. The more the tuning is altered, the greater will be the difference of phase, till at last it reaches the duration of a quarter of a vibration. The magnitude of the difference of phase agrees during this change precisely with the strength of the resonance, so that to a certain degree we are able to measure the former by the latter. If we represent the strength of the sound in the resonance chamber when in unison with the fork by 10, and divide the periodic time of a vibration, like the circumference of a circle, into 360 degrees, the relation between the strength of the resonance and the difference of phase is shewn by the following table : —
| Strength of Resonance | Difference of Phase in angular degrees |
| 10 | 0° |
| 9 | 35° 54' |
| 8 | 50° 12' |
| 7 | 60° 40' |
| 6 | 68° 54' |
| 5 | 75° 31' |
| 4 | 80° 48' |
| 3 | 84° 50' |
| 2 | 87° 42' |
| 1 | 89° 26' |
This table shews that a comparatively slight weakening of resonance by altering the tuning of the chamber occasions considerable differences of phase, but that when the weakening is considerable there are relatively slight changes of phase. We can take advantage of this circumstance when compounding the vowel sounds by means of the tuning-forks to produce every possible alteration of phase. It is only necessary to let the lid shade the mouth of the resonance chamber till the strength of the tone is perceptibly diminished. As soon as we have learned how to estimate roughly the amount of diminution of loudness, the above table gives us the corresponding alteration of phase. We are thus able to alter the vibrations of the tones in question to any amount, up to a quarter of the periodic time of a vibration. Alterations of phase to the amount of half the periodic time are produced by sending the electric current through the electro-magnets of the corresponding fork in an opposite direction, which causes the ends of the fork to be repelled instead of attracted by the electro-magnets on the passage of the current, and thus sets the fork vibrating in the contrary direction. This counter-excitement of the fork, however, by repelling currents, must not be continued too long, as the magnetism of the fork itself would otherwise gradually diminish, whereas attracting currents strengthen it or maintain it at a maximum. It is well known that the magnetism of masses of iron that are violently agitated is easily altered.
After a tone has been compounded, in which some of the partials have been weakened and at the same time altered in phase by the half-shading of the apertures of their corresponding resonance chambers, we can re-compound the same tone by an equal amount of weakening in the same partials, but without shading the aperture, and therefore without change of phase, by simply leaving the mouths of the chambers wide open, and increasing their distances from the exciting forks, until the required amount of enfeeblement of sound is attained.
For example, let us first sound the forks
In this manner every possible difference of phase in the tones of two chambers can be produced. The same process can of course be applied to any required number of forks. I have thus experimented upon numerous combinations of tone with varied differences of phase, and I have never experienced the slightest difference in the quality of tone. So far as the quality of tone was concerned, I found that it was entirely indifferent whether I weakened the separate partial tones by shading the mouths of their resonance chambers, or by moving the chamber itself to a sufficient distance from the fork. Hence the answer to the proposed question is: the quality of the musical portion of a compound tone depends solely on the number and relative strength of its partial simple tones, and in no respect on their differences of phase.[6]
The preceding proof that quality of tone is independent of difference of phase, is the easiest to carry out experimentally, but its force lies solely in the theoretical proposition that phases alter contemporaneously with strength of tone when the mouths of the resonance chambers are shaded, and this proposition is the result of mathematical theory alone. We cannot make vibrations of air directly visible. But by a slight change in the experiment it may be so conducted as to make the alteration of phase immediately visible. It is only necessary to put the tuning-forks themselves out of tune with their resonance chambers, by attaching little lumps of wax to the prongs. The same law holds for the phases of a tuning-fork kept in vibration by an electric current, as for the resonance chambers themselves. The phase gradually alters by a quarter period, while the strength of the tone of the fork is reduced from a maximum to nothing at all, by putting it out of tune. The phase of the motion of the air retains the same relation to the phase of the vibration of the fork, because the pitch, which is determined by the number of interruptions of the electrical current in a second, is not altered by the alteration of the fork. The change of phase in the fork can be observed directly by means of Lissajou's vibration microscope, already described and shewn in (fig. 22, p. 81). Place the prongs of the fork and the microscope of this instrument horizontally, and the fork to be examined vertically; powder the upper end of one of its prongs with a little starch, direct the microscope to one of the grains of starch, and excite both forks by means of the electrical currents of the interrupting fork (fig. 33, p. 122). The fork of Lissajou's instrument is in unison with the interrupting fork. The grain of starch vibrates horizontally, the object-glass of the microscope vertically, and thus, by the composition of these two motions, curves are generated, just as in the observations on violin strings previously described.
When the observed fork is in unison with the interrupting fork, the curve becomes an oblique straight line (fig. 34, 1), if both forks pass through their position of rest at the same moment. As the phase alters, the straight line passes through a long oblique ellipse (2, 3), till on the difference of phase becoming a quarter of a period, it develops into a circle (4); and then as the difference of phase increases, it passes through oblique ellipses (5, 6) in another direction, till it reaches another straight line (7), on the difference becoming half a period.

If the second fork is the upper Octave of the interrupting fork, the curves 1, 2, 3, 4, 5, in fig. 35, shew the series of forms. Here 3 answers to the case when both forks pass through their position of rest at the same time; 2 and 4 differ from that position by \(\tfrac{1}{12}\), and 1 and 5 by \(\tfrac14\) of a wave of the higher fork.

If we now bring the forks into the most perfect possible unison with the interrupting fork, so that both vibrate as strongly as possible, and then alter their tuning a little by putting on or removing pieces of wax, we also see one figure of the microscopic image gradually passing into another, and can thus easily assure ourselves of the correctness of the law already cited. Experiments on quality of tone are then conducted by first bringing all the forks as exactly as possible to the pitches of the harmonic upper partial tones of the interrupting fork, next removing the resonance chambers to such distances from the forks as will give the required relations of strength, and finally putting the forks out of tune as much as we please by sticking on lumps of wax. The size of these lumps should be previously so regulated by microscopical observation as to produce the required difference of phase. This, however, at the same time weakens the vibrations of the forks, and hence the strength of the tones must be restored to its former state by bringing the resonance chambers nearer to the forks.
The result in these experiments, where the forks are put out of tune, is the same as in those where the resonance chambers were put out of tune. There is no perceptible alteration of quality of tone. At least there is no alteration so marked as to be recognisable after the expiration of the few seconds necessary for resetting the apparatus, and hence certainly no such change of quality as would change one vowel into another.
An apparent exception to this rule must here be mentioned. If the forks \(B\flat\) and \(b\flat\) are not perfectly tuned as Octaves, and are brought into vibration by rubbing or striking, an attentive ear will observe very weak beats which appear like small changes in the strength of the tone and its quality. These beats are certainly connected with the successive entrance of the vibrating forks on varying difference of phase. Their explanation will be given when combinational tones are considered, and it will then be shewn that these slight variations of quality are referable to changes in the strength of one of the simple tones.
Hence we are able to lay down the important law that differences in musical quality of tone depend solely on the presence and strength of partial tones, and in no respect on the differences in phase under which these partial tones enter into composition. It must be here observed that we are speaking only of musical quality as previously defined. When the musical tone is accompanied by unmusical noises, such as jarring, scratching, soughing, whizzing, hissing, these motions are either not to be considered as periodic at all, or else correspond to high upper partials, of nearly the same pitch, which consequently form strident dissonances. We were not able to embrace these in our experiments, and hence we must leave it for the present doubtful whether in such dissonating tones difference of phase is an element of importance. Subsequent theoretic considerations will lead us to suppose that it really is.
If we wish only to imitate vowels by compound tones without being able to distinguish the differences of phase in the individual constituent simple tones, we can effect our purpose tolerably well with organ pipes. But we must have at least two series of them, loud open and soft stopped pipes, because the strength of tone cannot be increased by additional pressure of wind without at the same time changing the pitch. I have had a double row of pipes of this kind made by Herr Appunn in Hanau, giving the first sixteen partial tones of \(B\flat\). All these pipes stand on a common windchest, which also contains the valves by which they can be opened or shut. Two larger valves cut off the passage from the windchest to the bellows. While these valves are closed, the pipe valves are arranged for the required combination of tones, and then one of the main valves of the windchest is opened, allowing all the pipes to sound at once. The character of the vowel is better produced in this way by short jerks of sound, than by a long continued sound. It is best to produce the prime tone and the predominant upper partial tones of the required vowels on both the open and stopped pipes at once, and to open only the weak stopped pipes for the next adjacent tones, so that the strong tone may not be too isolated.
The imitation of the vowels by this means is not very perfect, because, among other reasons, it is impossible to graduate the strength of tone on the different pipes so delicately as on the tuning-forks, and the higher tones especially are too screaming. But the vowel sounds thus composed are perfectly recognisable.
We proceed now to consider the part played by the ear in the apprehension of quality of tone. The assumption formerly made respecting the function of the ear, was that it was capable of distinguishing both the pitch number of a musical tone (which gives the pitch), and also the form of the vibrations (on which the difference of quality depends). This last assertion was based simply on the exclusion of all other possible assumptions. As it could be proved that sameness of pitch always required equal pitch numbers, and as loudness visibly depended upon the amplitude of the vibrations, the quality of tone must necessarily depend on something which was neither the number nor the amplitude of the vibrations. There was nothing left us but form. We can now make this view more definite. The experiments just described shew that waves of very different forms (as fig. 31, C, D, p. 120, and fig. 12, C, D, p. 32), may have the same quality of tone, and indeed, for every case, except the simple tone, there is an infinite number of forms of wave of this kind, because any alteration of the difference of phase alters the form of wave without changing the quality of tone. The only decisive character of a quality of tone, is that the motion of the air which strikes the ear when resolved into a sum of pendulum vibrations gives the same degree of strength to the same simple vibration.
Hence the ear does not distinguish the different forms of waves in themselves, as the eye distinguishes the different vibrational curves. The ear must be said rather to decompose every wave form into simpler elements according to a definite law. It then receives a sensation from each of these simpler elements as from an harmonious tone. By trained attention the ear is able to become conscious of each of these simpler tones separately. And what the ear distinguishes as different qualities of tone are only different combinations of these simpler sensations.
The comparison between ear and eye is here very instructive. When the vibrational motion is rendered visible, as in the vibration microscope, the eye is capable of distinguishing every possible different form; of vibration one from another, even such as the ear cannot distinguish. But the eye is not capable of directly resolving the vibrations into simple vibrations, as the ear is. Hence the eye, assisted by the above-named instrument, really distinguishes the form of vibration, as such, and in so doing distinguishes every different form of vibration. The ear, on the other hand, does not distinguish every different form of vibration, but only such as when resolved into pendular vibrations, give different constituents. But on the other hand, by its capability of distinguishing and feeling these very constituents, it is again superior to the eye, which is quite incapable of so doing.
This analysis of compound into simple pendular vibrations is an astonishing property of the ear. The reader must bear in mind that when we apply the term 'compound' to the vibrations produced by a single musical instrument, the 'composition' has no existence except for our auditory perceptions, or for mathematical theory. In reality, the motion of the particles of the air is not at all compound, it is quite simple, flowing from a single source. When we turn to external nature for an analogue of such an analysis of periodical motions into simple motions, we find none but the phenomena of sympathetic vibration. In reality if we suppose the dampers of a pianoforte to be raised, and allow any musical tone to impinge powerfully on its sounding board, we bring a set of strings into sympathetic vibration, namely all those strings, and only those, which correspond with the simple tones contained in the given musical tone. Here, then, we have, by a purely mechanical process, a resolution of air waves precisely similar to that performed by the ear. The air wave, quite simple in itself, brings a certain number of strings into sympathetic vibration, and the sympathetic vibration of these strings depends on the same law as the sensation of harmonic upper partial tones in the ear.[7]
There is necessarily a certain difference between the two kinds of apparatus, because the pianoforte strings readily vibrate with their upper partials in sympathy, and hence separate into several vibrating sections. We will disregard this peculiarity in making our comparison. It would besides be easy to make an instrument in which the strings would not vibrate sensibly or powerfully for any but their prime tones, by simply loading the strings slightly in the middle. This would make their higher proper tones inharmonic to their primes.
Now suppose we were able to connect every string of a piano with a nervous fibre in such a manner that this fibre would be excited and experience a sensation every time the string vibrated. Then every musical tone which impinged on the instrument would excite, as we know to be really the case in the ear, a series of sensations exactly corresponding to the pendular vibrations into which the original motion of the air had to be resolved. By this means, then, the existence of each partial tone would be exactly so perceived, as it really is perceived by the ear. The sensations of simple tones of different pitch would under the supposed conditions fall to the lot of different nervous fibres, and hence be produced quite separately, and independently of each other.
Now, as a matter of fact, later microscopic discoveries respecting the internal construction of the ear, lead to the hypothesis, that arrangements exist in the ear similar to those which we have imagined. The end of every fibre of the auditory nerve is connected with small elastic parts, which we cannot but assume to be set in sympathetic vibration by the waves of sound.

The construction of the ear may be briefly described as follows : — The fine ends of the fibres of the auditory nerves are expanded on a delicate membrane in a cavity filled with fluid. Owing to its involved form this cavity is known as the labyrinth of the ear. To conduct the vibrations of the air with sufficient force into the fluid of the labyrinth is the office of a second portion of the ear, the tympănum or drum and the parts within it. Fig. 36 above is a diagrammatic section, of the size of life, shewing the cavities belonging to the auditory apparatus. A is the labyrinth, B B the cavity of the tympănum or drum, D the funnel-shaped entrance into the meātus or external auditory passage, narrowest in the middle and expanding slightly towards its upper extremity. This meātus, in the ear or passage, is a tube formed partly of cartilage or gristle and partly of bone, and it is separated from the tympănum or drum, by a thin circular membrane, the membrāna tympănī or drumskin[8] c c, which is rather laxly stretched in a bony ring. The drum (tym'pănum) B lies between the outer passage (meātus) and the labyrinth. The drum is separated from the labyrinth by bony walls, pierced with two holes, closed by membranes. These are the so-called windows (fenes'trae) of the labyrinth. The upper one o, called the oval window (fenes'tra ōvālis), is connected with one of the ossicles or little bones of the ear called the stirrup. The lower or round window r (fenes'tra rotun'da) has no connection with these ossicles.
The drum of the ear is consequently completely shut off from the external passage and from the labyrinth. But it has free access to the upper part of the pharynx or throat, through the so-called Eustachian[9] tube E, which in Germany is termed a trumpet, because of the trumpet-like expansion of its pharyngeal extremity and the narrowness of its opening into the drum. The end which opens into the drum is formed of bone, but the expanded pharyngeal end is formed of thin flexible cartilage or gristle, split along its upper side. The edges of the split are closed by a sinewy membrane. By closing the nose and mouth, and either condensing the air in the mouth by pressure, or rarefying it by suction, air can be respectively driven into or drawn out of the drum through this tube. At the entrance of air into the drum, or its departure from it, we feel a sudden jerk in the ear, and hear a dull crack. Air passes from the pharynx to the drum, or from the drum to the pharynx only at the moment of making the motion of swallowing. When the air has entered the drum it remains there, even after nose and mouth are opened again, until we make another motion of swallowing. Then the air leaves the drum, as we perceive by a second cracking in the ear, and the cessation of the feeling of tension in the drumskin which had remained up till that time. These experiments shew that the tube is not usually open, but is opened only during swallowing, and this is explained by the fact that the muscles which raise the vēlum palātī or soft palate, and are set in action on swallowing, arise partly from the cartilaginous extremity of the tube. Hence the drum is generally quite closed, and filled with air, which has a pressure equal to that of the external air, because it has from time to time, that is whenever we swallow, the means of equalising itself with the same by free communication. For a strong pressure of the air, the tube opens even without the action of swallowing, and its power of resistance seems to be very different in different individuals.
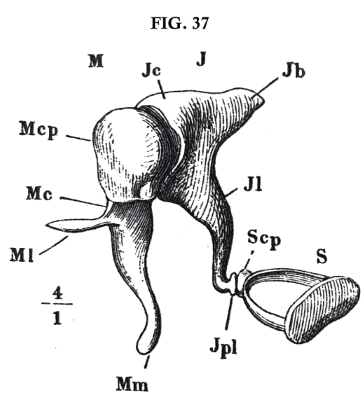
In two places, this air in the drum is likewise separated from the fluid of the labyrinth merely by a thin stretched membrane, which closes the two windows of the labyrinth, already mentioned, namely, the oval window (o, fig. 36, p. 129) and the round window (r). Both of these membranes are in contact on their outer side with the air of the drum, and on their inner side with the water of the labyrinth. The membrane of the round window is free, but that of the oval window is connected with the drumskin of the ear by a series of three little bones or auditory ossicles, jointed together. Fig. 37 shews the three ossicles in their natural connection, enlarged four diameters. They are the hammer (mal'leus) M, the anvil (in'cūs) J, and the stirrup (sta'pes[10]) S. The hammer is attached to the drumskin, and the stirrup to the membrane of the oval window.
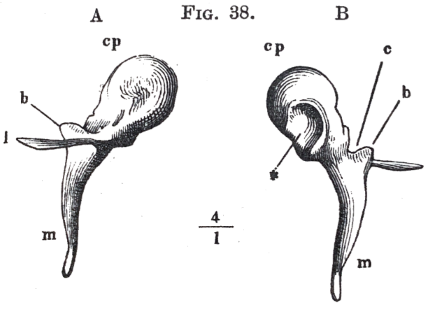
The hammer shewn separately in fig. 38, has a thick, rounded upper extremity, the head cp, and a thinner lower extremity, the handle m. Between these two is a contraction c, the neck. At the back of the head is the surface of the joint, by means of which it fits on to the anvil. Below the neck, where the handle begins, project two processes, the long l, also called processus Foliānus and pr. grăcĭlis, and the short b, also called pr. bre'vis. The long process has the proportionate length shewn in the figure, in children only; in adults it appears to be absorbed down to a little stump. It is directed forwards, and is covered by which fasten the hammer in front. The short process b, on the other hand, is directed towards the drumskin, and presses its upper part a little forwards. From the point of this process b to the point of the handle m the hammer is attached to the upper portion of the drumskin, in such a manner that the point of the handle draws the drumskin considerably towards the inner part of the ear.
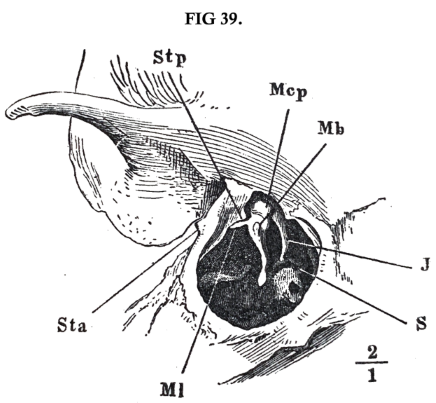

Fig. 39 above shews the hammer in its natural position as seen from without, after the drumskin has been removed, and fig. 40 shews the hammer lying against the drumskin as seen from within. The hammer is fastened along the upper margin of the drumskin by a fold of mucous membrane, within which run a series of rather stiff bundles of tendinous fibres. These straps arise in a line which passes from the processus Folianus (fig. 38, l), above the contraction of the neck, towards the lower end of the surface of the joint for the anvil, and in elderly people is developed into a prominent ridge of bone. The tendinous bands or ligaments are strongest and stiffest at the front and back end of this line of insertion. The front portion of the ligament, lig. mallei anterius (fig. 40, ma), surrounds the processus Folianus, and is attached partly to a bony spine (figs. 39 and 40, Stp) of the osseous ring of the drum, which projects close to the neck of the hammer, and partly to its under edge, and partly falls into a bony fissure which leads towards the articulation of the jaw. The back portion of the same ligament, on the other hand, is attached to a sharp-edged bony ridge projecting inwards from the drumskin, and parallel to it, a little above the opening, through which a traversing nerve, the chorda tympănī (fig. 40, l, l, p. 131), enters the bone. This second bundle of fibres may be called the lig. mallĕī posterĭus. In fig. 39 (p. 131) the origin of this ligament is seen as a little projection of the ring to which the drumskin is attached. This projection bounds towards the right the upper edge of the opening for the drumskin, which begins to the left of Stp, exactly at the place where the long process of the anvil makes its appearance in the figure. These two ligaments, front and back, taken together form a moderately tense sinewy chord, round which the hammer can turn as on an axis. Hence even when the two other ossicles have been carefully removed, without loosening these two ligaments, the hammer will remain in its natural position, although not so stiffly as before.
The middle fibres of the broad ligamentous band above mentioned pass outwards towards the upper bony edge of the drumskin. They are comparatively short and are known as lig. mallei externum. Arising above the line of the axis of the hammer, they prevent the head from turning too far inwards, and the handle with the drumskin from turning too far outwards, and oppose any down-dragging of the ligament forming the axis. The first effect is increased by a ligament (lig. mallei superiud) which passes from the processus Folianus, upwards, into the small slit, between the head of the hammer and the wall of the drum, as shewn in fig. 40 (p. 131).
It must be observed that in the upper part of the channel of the Eustachian tube, there is a muscle for tightening the drumskin (m. tensor tympănī), the tendon of which passes obliquely across the cavity of the drum and is attached to the upper part of the handle of the hammer (at *, fig. 40, p. 131). This muscle must be regarded as a moderately tense elastic band, and may have its tension temporarily much increased by active contraction. The effect of this muscle is also principally to draw the handle of the hammer inwards, together with the drumskin. But since its point of attachment is so close to the ligamentous axis, the chief part of its pull acts on this axis, stretching it as it draws it inwards. Here we must observe that in the case of a rectilinear inextensible cord, which is moderately tense, such as the ligamentous axis of the hammer, a slight force which pulls it sideways, suffices to produce a very considerable increase of tension. This is the case with the present arrangement of stretching muscles. It should also be remembered that quiescent muscles not excited by innervation, are always stretched elastically in the living body, and act like elastic bands. This elastic tension can of course be considerably increased by the innervation which brings the muscles into action, but such tension is never entirely absent from the majority of our muscles.
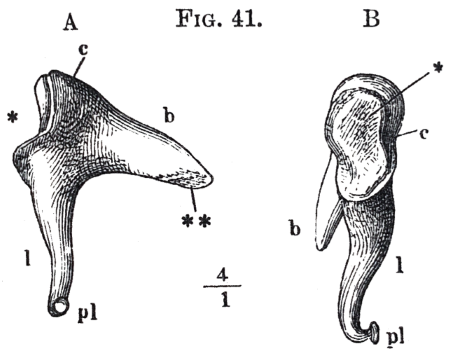
The anvil, which is shewn separately in fig. 41, resembles a double tooth with two fangs; the surface of its joint with the hammer (at *, fig. 41), replacing the masticating surface. Of the two roots of the tooth which are rather widely separated, the upper, directed backwards, is called the short process b; the other, thinner and directed downwards, the long process of the anvil l. At the tip of the latter is the knob which articulates with the stirrup. The tip of the short is of a short ligament and an imperfectly developed joint at its under surface, is connected with the back wall of the cavity of the drum, at the spot where this passes backwards into the air cavities of the mastoid process behind the ear. The joint between anvil and hammer is a curved depression of a rather irregular form, like a saddle. In its action it may be compared with the joints of the well-known Breguet watchkeys, which have rows of interlocking teeth, offering scarcely any resistance to revolution in one direction, but allowing no revolution whatever in the other. Interlocking teeth of this kind are developed upon the under side of the joint between hammer and anvil. The tooth on the hammer projects towards the drumskin, that of the anvil lies inwards; and, conversely, towards the upper end of the hollow of the joint, the anvil projects outwards, and the hammer inwards. The consequence of this arrangement is that when the hammer is drawn inwards by the handle, it bites the anvil firmly and carries it with it. Conversely, when the drumskin, with the hammer, is driven outwards, the anvil is not obliged to follow it. The interlocking teeth of the surfaces of the joint then separate, and the surfaces glide over each other with very little friction. This arrangement has the very great advantage of preventing any possibility of the stirrup's being torn away from the oval window, when the air in the auditory passage is considerably rarefied. There is also no danger from driving in the hammer, as might happen when the air in the auditory passage was condensed, because it is powerfully opposed by the tension of the drumskin, which is drawn in like a funnel.
When air is forced into the cavity of the drum in the act of swallowing, the contact of hammer and anvil is loosened. Weak tones in the middle and upper regions of the scale are then not heard much more weakly than usual, but stronger tones are very sensibly damped. This may perhaps be explained by supposing that the adhesion of the articulating surfaces suffices to transfer weak motions from one bone to the other, but that strong impulses cause the surfaces to slide over one another, and hence the tones due to such impulses must be enfeebled.
Deep tones are damped in this case, whether they are strong or weak, perhaps because these always require larger motions to become audible.[11]
Another important effect on the apprehension of tone, which is due to the above arrangement in the articulation of hammer and anvil, will have to be considered in relation to combinational tones. [See p. 158.]
Since the attachment of the tip of the short process of the anvil lies sensibly inwards and above the ligamentous axis of the hammer, the head of the hammer separates from the articulating surface between hammer and anvil, when the head is driven outwards, and therefore the handle and drumskin are driven inwards. The consequence is that the ligaments holding the anvil against the hammer, and on the tip of the short process of the anvil, are sensibly stretched, and hence the tip is raised from its osseous support. Consequently in the normal position of the ossicles for hearing, the anvil has no contact with any other bone but the hammer, and both bones are held in position only by stretched ligaments, which are tolerably tight, so that only the revolution of the hammer about its ligamentous axis remains comparatively free.
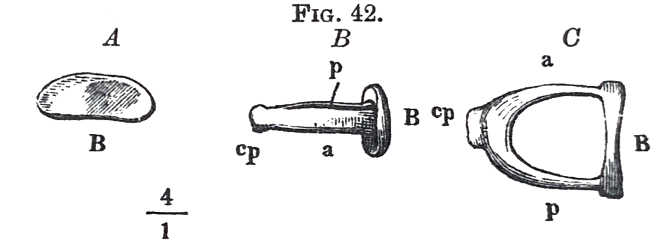
The third ossicle, the stirrup, shewn separately in fig. 42, has really a most striking resemblance to the implement after which it has been named. The foot B is fastened into the membrane of the oval window, and fills it all up, with the exception of a narrow margin. The head cp, has an articulating hole for the tip of the long process of the anvil (processus lenticulāris, or os orbiculāre). The joint is surrounded by a lax membrane. When the drumskin is normally drawn inwards, the anvil presses on the stirrup, so that no tighter ligamentous fastening of the joint is necessary. Every increase in the push on the hammer arising from the drumskin also occasions an increase in the push of the stirrup against the oval window; but in this action the upper and somewhat looser margin of its foot is more displaced than the under, so that the head rises slightly; this motion again causes a slight elevation of the tip of the long process in the anvil, in the direction conditioned by its position, inwards and underneath the ligamentous axis of the hammer.
The excursions of the foot of the stirrup are always very small, and according to my measurements[12] never exceed one-tenth of a millimetre (.00394 or about \(\tfrac{1}{254}\) of an inch). But the hammer when freed from anvil and stirrup, with its handle moving outwards, and sliding over the articulating surface of the anvil, can make excursions at least nine times as great as it can execute when acting in connection with anvil and stirrup.
The first advantage of the apparatus belonging to the drum of the ear, is that the whole sonorous motion of the comparatively wide surface of the drumskin (vertical diameter 9 to 10 millimetres [or 0.35 to 0.39 inches], just over one-third of an inch; horizontal diameter, 7.5 to 9 millimetres [or 0.295 to 0.35 inches], that is about five-sixths of the former dimensions) is collected and transferred by the ossicles to the relatively much smaller surface of the oval window or of the foot of the stirrup, which is only 1.5 to 3 millimetres [0.06 to 0.12 inches] in diameter. The surface of the drumskin is hence 15 to 20 times larger than that of the oval window.
In this transference of the vibrations of air into the labyrinth it is to be observed that though the particles of air themselves have a comparatively large amplitude of vibration, yet their density is so small that they have no very great moment of inertia, and consequently when their motion is impeded by the drumskin of the ear, they are not capable of presenting much resistance to such an impediment, or of exerting any sensible pressure against it. The fluid in the labyrinth, on the other hand, is much denser and heavier than the air in the auditory passage, and for moving it rapidly backwards and forwards as in sonorous oscillations, a far greater exertion of pressure is required than was necessary for the air in the auditory passage. On the other hand the amplitude of the vibrations performed by the fluid in the labyrinth are relatively very small, and extremely minute vibrations will in this case suffice to give a vibratory motion to the terminations and appendages of the nerves, which lie on the very limits of microscopic vision.
The mechanical problem which the apparatus within the drum of the ear had to solve, was to transform a motion of great amplitude and little force, such as impinges on the drumskin, into a motion of small amplitude and great force, such as had to be communicated to the fluid in the labyrinth.
A problem of this sort can be solved by various kinds of mechanical apparatus, such as levers, trains of pulleys, cranes, and the like. The mode in which it is solved by the apparatus in the drum of the ear, is quite unusual, and very peculiar.
A leverage is certainly employed, but only to a moderate extent. The tip of the handle of the hammer, on which the pull of the drumskin first acts, is about once and a half as far from the axis of rotation as that point of the anvil which presses on the stirrup (see fig. 39, p. 131). The handle of the hammer consequently forms the longer arm of a lever, and the pressure on the stirrup will be once and a half as great as that which drives in the hammer.
The chief means of reinforcement is due to the form of the drumskin. It has been already mentioned that its middle or navel (umbĭlīcus) is drawn inwards by the handle, so as to present a funnel shape. But the meridian lines of this funnel drawn from the navel to the circumference, are not straight lines; they are slightly convex on the outer side. A diminution of pressure in the auditory passage increases this convexity, and an augmentation diminishes it. Now the tension caused in an inextensible thread, having the form of a flat arch, by a force acting perpendicular to its convexity, is very considerable. It is well known that a sensible force must be exerted to stretch a long thin string into even a tolerably straight horizontal line. The force is indeed very much greater than the weight of the string which pulls the string from the horizontal position.[13] In the case of the drumskin, it is not gravity which prevents its radial fibres from straightening themselves, but partly the pressure of the air, and partly the elastic pull of the circular fibres of the membrane. The latter tend to contract towards the axis of the funnel-shaped membrane, and hence produce the inflection of the radial fibres towards this axis. By means of the variable pressure of air during the sonorous vibrations of the atmosphere this pull exerted by the circular fibres is alternately strengthened and weakened, and produces an effect on the point where the radial fibres are attached to the tip of the handle of the hammer, similar to that which would happen if we could alternately increase and diminish the weight of a string stretched horizontally, for this would produce a proportionate increase and decrease in the pull exerted by the hand which stretched it.
In a horizontally stretched string such as has been just described, it should be further remarked that an extremely small relaxation of the hand is followed by a considerable fall in the middle of the string. The relaxation of the hand, namely, takes place in the direction of the chord of the arc, and easy geometrical considerations shew that chords of arcs of the same length and different, but always very small curvature, differ very slightly indeed from each other and from the lengths of the arcs themselves.[14] This is also the case with the drumskin. An extremely little yielding in the handle of the hammer admits of a very considerable change in the curvature of the drumskin. The consequence is that, in sonorous vibrations, the parts of the drumskin which lie between the inner attachment of this membrane to the hammer and its outer attachment to the ring of the drum, are able to follow the oscillations of the air with considerable freedom, while the motion of the air is transmitted to the handle of the hammer with much diminished amplitude but much increased force. After this, as the motion passes from the handle of the hammer to the stirrup, the leverage already mentioned causes a second and more moderate reduction of the amplitude of vibration with corresponding increase of force.
We now proceed to describe the innermost division of the organ of hearing, called the labyrinth. Fig. 43 (p. 136) represents a cast of its cavity, as seen from different positions. Its middle portion, containing the oval window Fv (fenestra vestĭbŭlī) that receives the foot of the stirrup, is called the vestibule of the labyrinth. From the vestibule proceeds forwards and underwards, a spiral canal, the snail-shell or cochlĕa, at the entrance to which lies the round window Fc (fenestra cochlĕae), which is turned towards the cavity of the drum. Upwards and backwards, on the other hand, proceed three semicircular canals from the vestibule, the horizontal, front vertical and back vertical semicircular canals, each of which debouches with both its mouths in the vestibule, and each of which has at one end a bottle-shaped enlargement, or ampulla (ha, vaa, vpa). The aquaeductus vestĭbŭlī shewn in the figure, Av, appears (from Dr. Fr. E. Weber's investigations) to form a communication between the water of the labyrinth, and the spaces for lymph within the cranium. The rough places Tsf and * are casts of canals which introduce nerves.
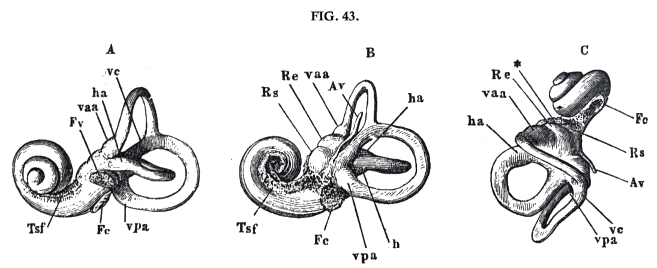
The whole of this cavity of the labyrinth is filled with fluid, and surrounded by the extremely hard close mass of the petrous bone, so that there are only two yielding spots on its walls, the two windows, the oval Fv, and the round Fc. Into the first, as already described, is fastened the foot of the stirrup, by a narrow membranous margin. The second is closed by a membrane. When the stirrup is driven against the oval window, the whole mass of fluid in the labyrinth is necessarily driven against the round window, as the only spot where its walls can give way. If, as Politzer did, we put a finely drawn glass tube as a manometer into the round window, without in other respects injuring the labyrinth, the water in this tube will be driven upwards as soon as a strong pressure of air acts on the outside of the drumskin and causes the foot of the stirrup to be driven into the oval window.
The terminations of the auditory nerve are spread over fine membranous formations, which lie partly floating and partly expanded in the hollow of the bony labyrinth, and taken together compose the membranous labyrinth. This last has on the whole the same shape as the bony labyrinth. But its canals and cavities are smaller, and its interior is divided into two separate sections; first the utrĭcŭlus with the semicircular canals, and second the saccŭlus with the membranous cochlĕa. Both the utriculus and the sacculus lie in the vestibule of the bony labyrinth; the utriculus opposite to the recessus elliptĭcus (Re, fig. 43 above), the sacculus opposite to the recessus sphaerĭcus (Rs). These are floating bags filled with water, and only touch the wall of the labyrinth at the point where the nerves enter them.

The form of the utriculus with its membranous semicircular canals is shewn in fig. 44. The ampullae project much more in the membranous than in the bony semicircular canals. According to the recent investigations of Rüdinger, the membranous semicircular canals do not float in the bony ones, but are fastened to the convex side of the latter. In each ampulla there is a pad-like prominence directed inwards, into which fibriles of the auditory nerve enter; and on the utriculus there is a place which is flatter and thickened. The peculiar manner in which the nerves terminate in this place will be described hereafter. Whether these, and the whole apparatus of the semicircular canals, assist in the sensation of hearing, has latterly been rendered very doubtful. [See p. 151.]
In the inside of the utriculus is found the auditory sand, consisting of little crystals of lime connected by means of a mucous mass with each other and with the thickened places where the nerves are so abundant. In the hollow of the bony vestibule, near the utriculus, and fastened to it, but not communicating with it, lies the sacculus, also provided with a similar thickened spot full of nerves. A narrow canal connects it with the canal of the membranous cochlea. As to the cavity of the cochlea, we see by fig. 43 opposite, that it is exactly similar to the shell of a garden snail; but the canal of the cochlea is divided into two almost completely separated galleries, by a transverse partition, partly bony and partly membranous. These galleries communicate only at the vertex of the cochlea through a small opening, the hĕlĭcotrēma, bounded by the hāmŭlus or hook-shaped termination of its central axis or mŏdĭ'lŏus. Of the two galleries into which the cavity of the bony cochlea is divided, one communicates directly with the vestibule and is hence called the vestibule gallery (scāla vestĭbŭlī). The other gallery is cut off from the vestibule by the membranous partition, but just at its base, where it begins, is the round window, and the yielding membrane, which closes this, allows the fluid in the gallery to exchange vibrations with the air in the drum. Hence this is called the drum gallery (scāla tympānī).

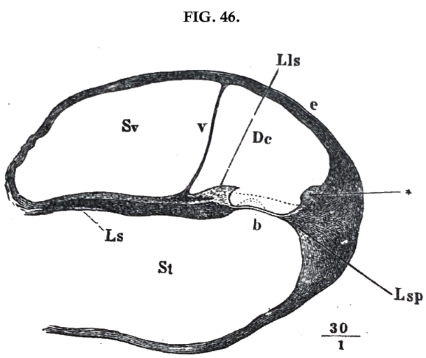
Finally, it must be observed that the membranous partition of the cochlea is not a single membrane, but a membranous canal (ductus cochleāris). Its inner margin is turned towards the central axis or mŏdĭŏlus, and attached to the rudimentary bony partition (lāmĭna spīrālis). A part of the opposite external surface is attached to the inner surface of the bony gallery. Fig. 45 shews the bony parts of a cochlea which has been laid open, and fig. 46 (p. 138), a transverse section of the canal (which is imperfect on the left hand at bottom). In both figures Ls denotes the bony part of the partition, and in fig. 46 v and b are the two unattached parts of the membranous canal. The transverse section of this canal is, as the figure shews, nearly triangular, so that an angle of the triangle near Lls is attached to the edge of the bony partition. The commencement of the ductus cochlearis at the base of the cochlea, communicates, as already stated, by means of a narrow membranous canal with the sacculus in the vestibule. Of the two unattached strips of its membranous walls, the one facing the vestibule gallery is a soft membrane, incapable of offering much resistance — Reissner's membrane (membrāna vestibulāris, v, fig. 46, p. 138); but the other, the membrāna băsĭlāris (b), is a firm, tightly stretched, elastic membrane, striped radially, corresponding to its radial fibres. It splits easily in the direction of these fibres, shewing that it is but loosely connected in a direction transverse to them. The terminations of the nerves of the cochlea and their appendages, are attached to the membrana băsĭlāris, as is shewn by the dotted lines in fig. 46.
When the drumskin is driven inwards by increased pressure of air in the auditory passage, it also forces the auditory ossicles inwards, as already explained, and as a consequence the foot of the stirrup penetrates deeper into the oval window. The fluid of the labyrinth, being surrounded in all other places by firm bony walls, has only one means of escape, — the round window with its yielding membrane. To reach it, the fluid of the labyrinth must either pass through the hĕlĭcŏtrēma, the narrow opening at the vertex of the cochlea, flowing over from the vestibule gallery into the drum gallery, or, as it would probably not have sufficient time to do this in the case of sonorous vibrations, press the membranous partition of the cochlea against the drum gallery. The converse action must take place when the air in the auditory passage is rarefied.
Hence the sonorous vibrations of the air in the outer auditory passage are finally transferred to the membranes of the labyrinth, more especially those of the cochlea, and to the expansions of the nerves upon them.
The terminal expansions of these nerves, as I have already mentioned, are connected with very small elastic appendages, which appear adapted to excite the nerves by their vibrations.

The nerves of the vestibule terminate in the thickened places of the bags of the membranous labyrinth, already mentioned (p. 137), where the tissue has a greater and almost cartilaginous consistency. One of these places, provided with nerves, projects like a fillet into the inner part of the ampulla of each semicircular canal, and another lies on each of the little bags in the vestibule. The nerve fibres here enter between the soft cylindrical cells of the fine cuticle (ĕpĭthēlĭum) which covers the internal surface of the fillets. Projecting from the internal surface of this epithelium in the ampullae, Max Schultze discovered a number of very peculiar, stiff, elastic hairs, shewn in fig. 47. They are much longer than the vibratory hairs of the ciliated epithe'lium (their length is \(\tfrac{1}{25}\) of a Paris line [or .00355 English inch] in the ray fish), brittle, and running to a very fine point. It is clear that fine stiff hairs of this kind are extremely well adapted for moving sympathetically with the motion of the fluid, and hence for producing mechanical irritation in the nerve fibres which lie in the soft epithelium between their roots.
According to Max Schultze, the corresponding thickened fillets in the vestibules, where the nerves terminate, have a similar soft epithelium, and have short hairs which are easily destroyed. Close to these surfaces which are covered with nerves, lie the calcareous concretions, called auditory stones (ōtŏlĭths), which in fishes form connected convexo-concave solids, shewing on their convex side an impression of the nerve fillet. In human beings, on the other hand, the otoliths are heaps of little crystalline bodies, of a longish angular form, lying close to the membrane of the little bags, and apparently attached to it. These otoliths seem also extremely well suited for producing a mechanical irritation of the nerves whenever the fluid in the labyrinth is suddenly agitated. The fine light membrane, with its interwoven nerves, probably instantly follows the motion of the fluid, whereas the heavier crystals are set more slowly in motion, and hence also yield up their motion more slowly, and thus partly drag and partly squeeze the adjacent nerves. This would satisfy the same conditions of exciting nerves, as Heidenhain's tetănomōtor. By this instrument the nerve which acts on a muscle is exposed to the action of a very rapidly oscillating ivory hammer, which at every blow squeezes without bruising the nerve. A powerful and continuous excitement of the nerve is thus produced, which is shewn by a powerful and continuous contraction of the corresponding muscle. The above parts of the ear seem to be well suited to produce similar mechanical excitement.
The construction of the cochlea is much more complex. The nerve fibres enter through the axis or modiolus of the cochlea into the bony part of the partition, and then come on to the membranous part. Where they reach this, peculiar formations were discovered quite recently (1851) by the Marchese Corti, and have been named after him. On these the nerves terminate.
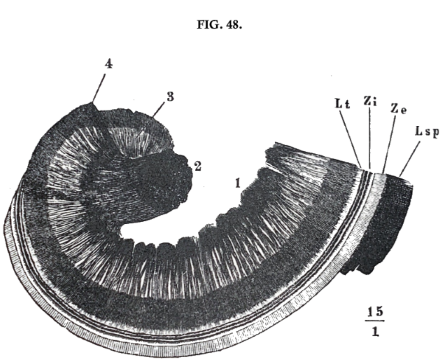
The expansion of the cochlean nerve is shewn in fig. 48. It enters through the axis (2) and sends out its fibres in a radial direction from the axis through the bony partition (1, 3, 4), as far as its margins. At this point the nerves pass under the commencement of the membrāna basilāris, penetrate this in a series of openings, and thus reach the ductus cochlearis and those nervous, elastic formations which lie on the inner zone (Zi) of the membrane.
The margin of the bony partition (a to b, fig. 49, p. 140), and the inner zone of the membrana basilaris (a a') are shewn after Hensen. The under side of the figure[15] corresponds with the scala tympăni, the upper with the ductus cochlearis. Here h at the top and k at the bottom, are the two plates of the bony partition, between which the expansion of the nerve b proceeds. The upper side of the bony partition bears a fillet of close ligamentous tissue (Z, fig. 49, also shewn at Lis, fig. 46, p. 138), which, on account of the toothlike impressions on its upper side, is called the toothed layer (zo'na denticula'ta), and which carries a peculiar elastic pierced membrane, Corti's membrane, M.C. fig. 49. This membrane is stretched parallel to the membrana basilaris as far as the bony wall on the outer side of the duct, and is there attached a little above the other. Between these two membranes lie the parts in and on which the nerve fibres terminate.

Among these Corti's arches (over g in fig. 49) are relatively the most solid formations. The series of these contiguous arches consists of two series of rods or fibres, an external and an internal. A single pair of these is shewn in fig. 50, A, below, and a short series of them in fig. 50, B, attached to the membrana basilaris, and at \(\dag\) also connected with the pierced tissue, into which fit the terminal cells of the nerves (fig. 49), which will be more fully described presently. These formations are shewn in fig. 51, (p. 141), as seen from the vestibule gallery; a is the denticulated layer, c the openings for the nerves on the internal margin of the membrana basilaris, its external margin being visible at u u; d is the inner series of Corti's rods, e the outer; over these, between e and x is seen the pierced membrane, against which lie the terminal cells of the nerves.
The fibres of the first, or outer series, are flat, somewhat S-shaped formations, having a swelling at the spot where they rise from the membrane to which they are attached, and ending in a kind of articulation which serves to connect them with the second or inner series. In fig. 51, p. 141, at d will be seen a great number of these ascending fibres, lying beside each other in regular succession. In the same way they may be seen all along the membrane of the cochlea, close together, so that there must be many thousands of them. Their sides lie close together, and even seem to be connected, leaving however occasional gaps in the line of connection, and these gaps are probably traversed by nerve fibres. Hence the fibres of the first series as a whole form a stiff layer, which endeavours to erect itself when the natural fastenings no longer resist, but allows the membrane on which they stand to crumple up between the attachments d and e of Corti's arches.
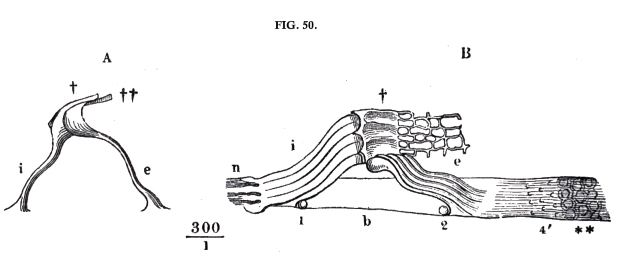
The fibres of the second or inner series, which form the descending part of the arch e, fig. 50, below, are smooth, flexible, cylindrical threads with thickened ends. The upper extremity forms a kind of joint to connect them with the fibres of the first series, the lower extremity is enlarged in a bell shape and is attached closely to the membrane at the base. In the microscopic preparations they generally appear bent in various ways ; but there can be no doubt that in their natural condition they are stretched with some degree of tension, so that they pull down the upper jointed ends of the fibres of the first series. The fibres of the first series arise from the inner margin of the membrane, which can be relatively little agitated, but the fibres of the second series are attached nearly in the middle of the membrane, and this is precisely the place where its vibrations will have the greatest excursions. When the pressure of the fluid in the drum gallery of the labyrinth is increased by driving the foot of the stirrup against the oval window, the membrane at the base of the arches will sink downwards, the fibres of the second series be more tightly stretched, and perhaps the corresponding places of the fibres of the first series be bent a little downwards. It does not, however, seem probable that the fibres of the first series themselves move to any great extent, for their lateral connections are strong enough to make them hang together in masses like a membrane, when they have been released from their attachment in anatomical preparations. On reviewing the whole arrangement, there can be no doubt that Corti's organ is an apparatus adapted for receiving the vibrations of the membrana basilaris, and for vibrating of itself, but our present knowledge is not sufficient to determine with accuracy the manner in which these vibrations take place. For this purpose we require to estimate the stability of the several parts and the degree of tension and flexibility, with more precision than can be deduced from such observations as have hitherto been made on isolated parts, as they casually group themselves under the microscope.

Now Corti's fibres are wound round and covered over with a multitude of very delicate, frail formations, fibres and cells of various kinds, partly the finest terminational runners of nerve fibres with appended nerve cells, partly fibres or ligamentous tissue, which appear to serve as a support for fixing and suspending the nerve formations.
The connection of these parts is best shewn in fig. 49 opposite. They are grouped like a pad of soft cells on each side of and within Corti's arches. The most important of them appear to be the cells c and d, which are furnished with hairs, precisely resembling the ciliated cells in the ampullae and utriculus. They appear to be directly connected by fine varicose nerve fibres, and constitute the most constant part of the cochlean formations; for with birds and reptiles, where the structure of the cochlea is much simpler, and even Corti's arches are absent, these little ciliated cells are always to be found, and their hairs are so placed as to strike against Corti's membrane during the vibration of the membrana basilaris. The cells at a and a', fig. 49 (p. 140), which appear in an enlarged condition at b and n in fig. 51 (p. 141), seem to have the character of an epithelium. In fig. 51 there will also be observed bundles and nets of fibres, which may be partly merely supporting fibres of a ligamentous nature, and may partly, to judge by their appearance as strings of beads, possess the character of bundles of the finest fibriles of nerves. But these parts are all so frail and delicate that there is still much doubt as to their connection and office.
The essential result of our description of the ear may consequently be said to consist in having found the terminations of the auditory nerves everywhere connected with a peculiar auxiliary apparatus, partly elastic, partly firm, which may be put in sympathetic vibration under the influence of external vibration, and will then probably agitate and excite the mass of nerves. Now it was shewn in Chap. III., that the process of sympathetic vibration was observed to differ according as the bodies put into sympathetic vibration were such as when once put in motion continued to sound for a long time, or soon lost their motion, p. 39. Bodies which, like tuning-forks when once struck, go on sounding for a long time, are susceptible of sympathetic vibration in a high degree notwithstanding the difficulty of putting their mass in motion, because they admit of a long accumulation of impulses in themselves minute, produced in them by each separate vibration of the exciting tone. But precisely for this reason there must be the exactest agreement between the pitches of the proper tone of the fork and of the exciting tone, because otherwise subsequent impulses given by the motion of the air could not constantly recur in the same phase of vibration, and thus be suitable for increasing the subsequent effect of the preceding impulses. On the other hand if we take bodies for which the tone rapidly dies away, such as stretched membranes or thin light strings, we find that they are not only susceptible of sympathetic vibration, when vibrating air is allowed to act on them, but that this sympathetic vibration is not so limited to a particular pitch, as in the other case, and they can therefore be easily set in motion by tones of different kinds. For if an elastic body on being once struck and allowed to sound freely, loses nearly the whole of its motion after ten vibrations, it will not be of much importance that any fresh impulses received after the expiration of this time, should agree exactly with the former, although it would be of great importance in the case of a sonorous body for which the motion generated by the first impulse would remain nearly unchanged up to the time that the second impulse was applied. In the latter case the second impulse could not increase the amount of motion, unless it came upon a phase of the vibration which had precisely the same direction of motion as itself.
The connection between these two relations can be calculated independently of the nature of the body put into sympathetic vibration,[16] and as the results are important to enable us to form a judgment on the state of things going on in the ear, a short table is annexed. Suppose that a body which vibrates sympathetically has been set into its state of maximum vibration by means of an exact unison, and that the exciting tone is then altered till the sympathetic vibration is reduced to of its former amount. The amount of the required difference of pitch is given in the first column in terms of an equally tempered Tone [which is \(\tfrac16\) of an Octave). Now let the same sonorous body be struck, and let its sound be allowed to die away gradually. The number of vibrations which it has made by the time that its intensity is reduced to \(\tfrac{1}{10}\) of its original amount is noted, and given in the second column.
| Difference of Pitch, in terms of an equally tempered Tone, necessary to reduce the intensity of sympathetic vibration to \(\tfrac{1}{10}\) of that produced by perfect unisonance | Number of vibrations after which the intensity of tone in a sonorous body whose sound is allowed to die out, reduces to \(\tfrac{1}{10}\) of its original amount |
| 1. One eighth of a Tone | 38.00 |
| 2. One Quarter of a Tone | 19.00 |
| 3. One Semiton | 9.50 |
| 4. Three quarters of a Tone | 6.33 |
| 5. A whole Tone | 4.75 |
| 6. A Tone and a quarter | 3.80 |
| 7. A tempered minor Third or a Tone and a half | 3.17 |
| 8. A Tone and three quarters | 2.71 |
| 9. A tempered major Third or two whole Tones | 2.37 |
Now, although we are not able exactly to discover how long the ear and its individual parts, when set in motion, will continue to sound, yet well-known experiments allow us to form some sort of judgment as to the position which the parts of the ear must occupy in the scale exhibited in this table. Thus, there cannot possibly be any parts of the ear which continue to sound so long as a tuning-fork, for that would be patent to the commonest observation. But even if there were any parts in the ear answering to the first degree of our table, that is requiring 38 vibrations to be reduced to \(\tfrac{1}{10}\) of their force, — we should recognise this in the deeper tones, because 38 vibrations last \(\tfrac13\) of a second for A, \(\tfrac16\) for a, \(\tfrac{1}{12}\) for a', &c., and such a long endurance of sensible sound would render rapid musical passages impossible in the unaccented and once-accented Octaves. Such a state of things would disturb musical effect as much as the strong resonance of a vaulted room, or as raising the dampers on a piano. When making a shake, we can readily strike 8 or 10 notes in a second, so that each tone separately is struck from 4 to 5 times. If, then, the sound of the first tone had not died off in our ear before the end of the second sound, at least to such an extent as not to be sensible when the latter was sounding, the tones of the shake, instead of being individually distinct, would merge into a continuous mixture of both. Now shakes of this kind, with 10 tones to a second, can be clearly and sharply executed throughout almost the whole scale, although it must be owned that from A downwards, in the great and contra Octaves they sound bad and rough, and their tones begin to mix. Yet it can be easily shewn that this is not due to the mechanism of the instrument. Thus if we execute a shake on the harmonium, the keys of the lower notes are just as accurately constructed and just as easy to move as those of the higher ones. Each separate tone is completely cut off with perfect certainty at the moment the valve falls on the air passage, and each speaks at the moment the valve is raised, because during so brief an interruption the tongues remain in a state of vibration. Similarly for the violoncello. At the instant when the finger which makes the shake falls on the string, the latter must commence a vibration of a different periodic time, due to its length; and the instant that the finger is removed, the vibration belonging to the deeper tone must return. And yet the shake in the bass is as imperfect on the violoncello as on any other instrument. Runs and shakes can be relatively best executed on a pianoforte because, at the moment of striking, the new tone sounds with great but rapidly decreasing intensity. Hence, in addition to the inharmonic noise produced by the simultaneous continuance of the two tones, we also hear a distinct prominence given to each separate tone. Now, since the difficulty of shaking in the bass is the same for all instruments, and for individual instruments is demonstrably independent of the manner in which the tones are produced, we are forced to conclude that the difficulty lies in the ear itself. We have, then, a plain indication that the vibrating parts of the ear are not damped with sufficient force and rapidity to allow of successfully effecting such a rapid alternation of tones.
Play a note to hear a trill from that note and the note a semitone above it or the note a semitone below it, if you played the highest note.
Nay more, this fact further proves that there must be different parts of the ear which are set in vibration by tones of different pitch and which receive the sensation of these tones. Thus, it might be supposed that as the vibratory mass of the whole ear, the drumskin, auditory ossicles, and fluid in the labyrinth, were vibrating at the same time, the inertia of this mass was the cause why the sonorous vibrations in the ear were not immediately extinguished. But this hypothesis would not suffice to explain the fact observed. For an elastic body set into sympathetic vibration by any tone, vibrates sympathetically in the pitch number of the exciting tone; but as soon as the exciting tone ceases, it goes on sounding in the pitch number of its own proper tone. This fact, which is derived from theory, may be perfectly verified on tuning-forks by means of the vibration microscope.
If, then, the ear vibrated as a single system, and were capable of continuing its vibration for a sensible time, it would have to do so with its own pitch number, which is totally independent of the pitch number of the former exciting tone. The consequence is that shakes would be equally difficult upon both high and low tones, and next that the two tones of the shake would not mix with each other, but that each would mix with a third tone, due to the ear itself. We became acquainted with such a tone in the last chapter, the high \(f''''\), p. 116. The result, then, under these circumstances would be quite different from what is observed.
Now if a shake of 10 notes in a second, be made on A, of which the vibrational number is 110, this tone would be
struck every \(\tfrac15\) of a second. We may justly assume that the shake would not be clear, if the intensity of
the expiring tone were not reduced to \(\tfrac{1}{10}\) of its original amount in this \(\tfrac15\) of a second. In
this case, after at least 22 vibrations, the parts of the ear which vibrate sympathetically with A must descend to
at least \(\tfrac{1}{10}\) of their intensity of vibration as their tone expires, so that their power of sympathetic
vibration cannot be of the first degree in the table on p. 143, but may belong to the second,
third, or some other higher degree. That the degree cannot be any much higher one, is shewn in the first place by
the fact that shakes and runs begin to be difficult even on tones which do not lie much lower. This we shall see by
observations on beats subsequently detailed. We may on the whole assume that the parts of the ear which vibrate
sympathetically have an amount of damping power corresponding to the third degree of our table, where the intensity
of sympathetic vibration with a Semitone difference of pitch is only \(\tfrac{1}{10}\) of what it is for a complete
unison. Of course there can be no question of exact determinations, but it is important for us to be able to form at
least an approximate conception of the influence of damping on the sympathetic vibration of the ear, as it has great
significance in the relations of consonance. Hence when we hereafter speak of individual parts of the ear vibrating
sympathetically with a determinate tone, we mean that they are set into strongest motion by that tone, but are also
set into vibration less strongly by tones of nearly the same pitch, and that this sympathetic vibration is still
sensible for the interval of a Semitone.

| Difference of Pitch | Intensity of Sympathetic Vibration | Difference of Pitch | Intensity of Sympathetic Vibration |
| 0.0 | 100 | 0.6 | 7.2 |
| 0.1 | 74 | 0.7 | 5.4 |
| 0.2 | 41 | 0.8 | 4.2 |
| 0.3 | 24 | 0.9 | 3.3 |
| 0.4 | 15 | Whole Tone | 2.7 |
| Semitone | 10 |
Now we cannot precisely ascertain what parts of the ear actually vibrate sympathetically with individual tones.[17] We can only conjecture what they are at present in the case of human beings and mammals. The whole construction of the partition of the cochlea, and of Corti's arches which rest upon it, appears most suited for executing independent vibrations. We do not need to require of them the power of continuing their vibrations for a long time without assistance.
But if these formations are to serve for distinguishing tones of different pitch, and if tones of different pitch are to be equally well perceived in all parts of the scale, the elastic formations in the cochlea, which are connected with different nerve fibres, must be differently tuned, and their proper tones must form a regularly progressive series of degrees through the whole extent of the musical scale.
Central spring has resonant frequency matchd to middle C on the keyboard. Others differ from their neighbors by a quarter tone (50 cents).
According to the recent anatomical researches of V. Hensen and C. Hasse, it is probably the breadth of the membrana basilaris in the cochlea, which determines the tuning.[18] At its commencement opposite the oval window, it is comparatively narrow, and it continually increases in width as it approaches the apex of the cochlea. The following measurements of the membrane in a newly born child, from the line where the nerves pass through on the inner edge, to the attachment to the ligamentum spirale on the outer edge, are given by V. Hensen: —
| Place of Section | Breadth of Membrane or Length of Transverse Fibres | |
| Millimetres | Inches | |
| 0.2625 mm [=0.010335 in.] from root | 0.04125 | .00162 |
| 0.8626 mm [=0.033961 in.] from root | 0.0825 | .00325 |
| Middle of the first spire | 0.169 | .00665 |
| End of first spire | 0.3 | .01181 |
| Middle of second spire | 0.41215 | .01624 |
| End of second spire | 0.45 | .01772 |
| At the hamulus | 0.495 | .01949 |
The breadth therefore increases more than twelvefold from the beginning to the end.
Corti's rods also exhibit an increase of size as they approach the vertex of the cochlea, but in a much less degree than the membrana basilaris. The following are Hensen’s measurements: —
| at the round window | at the hamulus | |||
| mm. | inch | mm. | inch | |
| Length of inner rod | 0.048 | 0.00189 | 0.0855 | 0.00337 |
| length of outer rod | 0.048 | 0.00189 | 0.098 | 0.00386 |
| Span of the arch | 0.019 | 0.00075 | 0.085 | 0.00335 |
Hence it follows, as Henle has also proved, that the greatest increase of breadth falls on the outer zone of the basilar membrane, beyond the line of the attachment of the outer rods. This increases from 0.023 mm. [= .000905 in.] to 0.41 mm. [= .016142 inch] or nearly twentyfold.
In accordance with these measures, the two rows of Corti's rods are almost parallel and upright near to the round window, but they are bent much more strongly towards one another near the vertex of the cochlea.
It has been already mentioned that the membrana basilaris of the cochlea breaks easily in the radial direction, but that its radial fibres have considerable tenacity. This seems to me to furnish a very important mechanical relation, namely, that this membrane in its natural connection admits of being tightly stretched in the transverse direction from the modiolus to the outer wall of the cochlea, but can have only little tension in the direction of its length, because it could not resist a strong pull in this direction.
Now the mathematical theory of the vibration of a membrane with different tensions in different directions shews that it behaves very differently from a membrane which has the same tension in all directions.[19] On the latter, vibrations produced in one part, spread uniformly in all directions, and hence if the tension were uniform it would be impossible to set one part of the basilar membrane in vibration, without producing nearly as strong vibrations (disregarding individual nodal lines) in all other parts of the membrane.
But if the tension in direction of its length is infinitesimally small in comparison with the tension in direction of the breadth, then the radial fibres of the basilar membrane may be approximatively regarded as forming a system of stretched strings, and the membranous connection as only serving to give a fulcrum to the pressure of the fluid against these strings. In that case the laws of their motion would be the same as if every individual string moved independently of all the others, and obeyed, by itself, the influence of the periodically alternating pressure of the fluid of the labyrinth contained in the vestibule gallery. Consequently any exciting tone would set that part of the membrane into sympathetic vibration, for which the proper tone of one of its radial fibres that are stretched and loaded with the various appendages already described, corresponds most nearly with the exciting tone; and thence the vibrations will extend with rapidly diminishing strength on to the adjacent parts of the membrane. Fig. 52, on p. 144, might be taken to represent, on an exaggerated scale of height, a longitudinal section of that part of the basilar membrane in which the proper tone of the radial fibres of the membrane are nearest to the exciting tone.
The strongly vibrating parts of the membrane would, as has been explained in respect to all bodies which vibrate sympathetically, be more or less limited, according to the degree of damping power in the adjacent parts, by friction against the fluid in the labyrinth and in the soft gelatinous parts of the nerve fillet.
Under these circumstances the parts of the membrane in unison with higher tones must be looked for near the round window, and those with the deeper, near the vertex of the cochlea, as Hensen also concluded from his measurements. That such short strings should be capable of corresponding with such deep tones, must be explained by their being loaded in the basilar membrane with all kinds of solid formations; the fluid of both galleries in the cochlea must also be considered as weighting the membrane, because it cannot move without a kind of wave motion in that fluid.
The observations of Hasse shew that Corti's arches do not exist in the cochlea of birds and amphibia, although the other essential parts of the cochlea, as the basilar membrane, the ciliated cells in connection with the terminations of the nerves, and Corti's membrane, which stands opposite the ends of these ciliae, are all present. Hence it becomes very probable that Corti's arches play only a secondary part in the function of the cochlea. Perhaps we might look for the effect of Corti's arches in their power, as relatively firm objects, of transmitting the vibrations of the basilar membrane to small limited regions of the upper part of the relatively thick nervous fillet, better than it could be done by the immediate communication of the vibrations of the basilar membrane through the soft mass of this fillet. Close to the outside of the upper end of the arch, connected with it by the stiffer fibriles of the membrana reticulāris, are the ciliated cells of the nervous fillet (see c in fig. 49, p. 140). In birds, on the other hand, the ciliated cells form a thin stratum upon the basilar membrane, and this stratum can readily receive limited vibrations from the membrane, without communicating them too far sideways.
According to this view Corti's arches, in the last resort, will be the means of transmitting the vibrations received from the basilar membrane to the terminal appendages of the conducting nerve. In this sense the reader is requested hereafter to understand references to the vibrations, proper tone, and intonation of Corti’s arches; the intonation meant is that which they receive through their connection with the corresponding part of the basilar membrane.
According to Waldeyer there are about 4500 outer arch fibres in the human cochlea. If we deduct 300 for the simple tones which lie beyond musical limits, and cannot have their pitch perfectly apprehended, there remain 4200 for the seven octaves of musical instruments, that is, 600 for every Octave, 50 for every Semitone [that is, 1 for every 2 cents]; certainly quite enough to explain the power of distinguishing small parts of a Semitone.[20] According to Prof. W. Breyer's investigations,[21] practised musicians can distinguish with certainty a difference of pitch arising from half a vibration in a second, in the doubly accented Octave. This would give 1000 distinguishable degrees of pitch in the Octave, from 500 to 1000 vibrations in the second. Towards the limits of the scale the power to distinguish differences diminishes. The 4200 Corti's arches appear then, in this respect, to be enough to apprehend distinctions of this amount of delicacy. But even if it should be found that many more than 4200 degrees of pitch could be distinguished in the Octave, it would not prejudice our assumption. For if a simple tone is struck having a pitch between those of two adjacent Corti's arches, it would set them both in sympathetic vibration, and that arch would vibrate the more strongly which was nearest in pitch to the proper tone. The smallness of the interval between the pitches of two fibres still distinguishable, will therefore finally depend upon the delicacy with which the different forces of the vibrations excited can be compared And we have thus also an explanation of the fact that as the pitch of an external tone rises continuously, our sensations also alter continuously and not by jumps, as must be the case if only one of Corti's arches were set in sympathetic motion at once.
To draw further conclusions from our hypothesis, when a simple tone is presented to the ear, those Corti's arches which are nearly or exactly in unison with it will be strongly excited, and the rest only slightly or not at all. Hence every simple note of determinate pitch will be felt only by certain nerve fibres, and simple tones of different pitch will excite different fibres. When a compound musical tone or chord is presented to the ear, all those elastic bodies will be excited, which have a proper pitch corresponding to the various individual simple tones contained in the whole mass of tones, and hence by properly directing attention, all the individual sensations of the individual simple tones can be perceived. The chord must be resolved into its individual compound tones, and the compound tone into its individual harmonic partial tones.
This also explains how it is that the ear resolves a motion of the air into pendular vibrations and no other. Any particle of air can of course execute only one motion at one time. That we considered such a motion mathematically as a sum of pendular vibrations, was in the first instance merely an arbitrary assumption to facilitate theory, and had no meaning in nature. The first meaning in nature that we found for this resolution came from considering sympathetic vibration, when we discovered that a motion which was not pendular, could produce sympathetic vibrations in bodies of those different pitches, which corresponded to the harmonic upper partial tones. And now our hypothesis has also reduced the phenomenon of hearing to that of sympathetic vibration, and thus furnished a reason why an originally simple periodic vibration of the air produces a sum of different sensations, and hence also appears as compound to our perceptions.
The sensation of different pitch would consequently be a sensation in different nerve fibres. The sensation of a quality of tone would depend upon the power of a given compound tone to set in vibration not only those of Corti’s arches which correspond to its prime tone, but also a series of other arches, and hence to excite sensation in several different groups of nerve fibres.
Physiologically it should be observed that the present assumption reduces sensations which differ qualitatively according to pitch and quality of tone, to a difference in the nerve fibres which are excited. This is a step similar to that taken in a wider field by Johannes Muller in his theory of the specific energies of sense. He has shewn that the difference in the sensations due to various senses, does not depend upon the actions which excite them, but upon the various nervous arrangements which receive them. We can convince ourselves experimentally that in whatever manner the optic nerve and its expansion, the retina of the eye, may be excited, by light, by twitching, by pressure, or by electricity, the result is never anything but a sensation of light, and that the tactual nerves, on the contrary, never give us sensations of light or of hearing or of taste. The same solar rays which are felt as light by the eye, are felt by the nerves of the hand as heat; the same agitations which are felt by the hand as twitterings, are tone to the ear.
Play a key and see if you can detect the difference in tone.
Just as the ear apprehends vibrations of different periodic time as tones of different pitch, so does the eye perceive luminiferous vibrations of different periodic time as different colours, the quickest giving violet and blue, the mean green and yellow, the slowest red. The laws of the mixture of colours led Thomas Young to the hypothesis that there were three kinds of nerve fibres in the eye, with different powers of sensation, for feeling red, for feeling green, and for feeling violet. In reality this assumption gives a very simple and perfectly consistent explanation of all the optical phenomena depending on colour. And by this means the qualitative differences of the sensations of sight are reduced to differences in the nerves which receive the sensations. For the sensations of each individual fibre of the optic nerve there remains only the quantitative differences of greater or less irritation.
The same result is obtained for hearing by the hypothesis to which our investigation of quality of tone has led us. The qualitative difference of pitch and quality of tone is reduced to a difference in the fibres of the nerves receiving the sensation, and for each individual fibre of the nerve there remains only the quantitative differences in the amount of excitement.
The processes of irritation within the nerves of the muscles, by which their contraction is determined, have hitherto been more accessible to physiological investigation than those which take place in the nerves of sense. In those of the muscle, indeed, we find only quantitative differences of more or less excitement, and no qualitative differences at all. In them we are able to establish, that during excitement the electrically active particles of the nerves undergo determinate changes, and that these changes ensue in exactly the same way whatever be the excitement which causes them. But precisely the same changes also take place in an excited nerve of sense, although their consequence in this case is a sensation, while in the other it was a motion; and hence we see that the mechanism of the process of irritation in the nerves of sense must be in every respect similar to that in the nerves of motion. The two hypotheses just explained really reduce the processes in the nerves of man’s two principal senses, notwithstanding their apparently involved qualitative differences of sensations, to the same simple scheme with which we are familiar in the nerves of motion. Nerves have been often and not unsuitably compared to telegraph wires. Such a wire conducts one kind of electric current and no other; it may be stronger, it may be weaker, it may move in either direction; it has no other qualitative differences. Nevertheless, according to the different kinds of apparatus with which we provide its terminations, we can send telegraphic despatches, ring bells, explode mines, decompose water, move magnets, magnetise iron, develop light, and so on. So with the nerves. The condition of excitement which can be produced in them, and is conducted by them, is, so far as it can be recognised in isolated fibres of a nerve, everywhere the same, but when it is brought to various parts of the brain, or the body, it produces motion, secretions of glands, increase and decrease of the quantity of blood, of redness and of warmth of individual organs, and also sensations of light, of hearing, and so forth. Supposing that every qualitatively different action is produced in an organ of a different kind, to which also separate fibres of nerve must proceed, then the actual process of irritation in individual nerves may always be precisely the same, just as the electrical current in the telegraph wires remains one and the same notwithstanding the various kinds of effects which it produces at its extremities. On the other hand, if we assume that the same fibre of a nerve is capable of conducting different kinds of sensation, we should have to assume that it admits of various kinds of processes of irritation, and this we have been hitherto unable to establish.
In this respect then the view here proposed, like Young’s hypothesis for the difference of colours, has a still wider signification for the physiology of the nerves in general.
Since the first publication of this book, the theory of auditory sensation here explained, has received an interesting confirmation from the observations and experiments made by V. Hensen[22] on the auditory apparatus of the Crustaceae. These animals have bags of auditory stones (otoliths), partly closed, partly opening outwards, in which these stones float freely in a watery fluid and are supported by hairs of a peculiar formation, attached to the stones at one end, and, partly, arranged in a series proceeding in order of magnitude, from larger and thicker to shorter and thinner. In many crustaceans also we find precisely similar hairs on the open surface of the body, and these must be considered as auditory hairs. The proof that these external hairs are also intended for hearing, depends first on the similarity of their construction with that of the hairs in the bags of otoliths; and secondly on Hensen's discovery that the sensation of hearing remained in the Mysis (opossum shrimp) when the bags of otoliths had been extirpated, and the external auditory hairs of the antennae were left.
Hensen conducted the sound of a keyed bugle through an apparatus formed on the model of the drumskin and auditory ossicles of the ear into the water of a little box in which a specimen of Mysis was fastened in such a way as to allow the external auditory hairs of the tail to be observed. It was then seen that certain tones of the horn set certain hairs into strong vibration, and other tones other hairs. Each hair answered to several notes of the horn, and from the notes mentioned we can approximatively recognise the series of under tones of one and the same simple tone. The results could not be quite exact, because the resonance of the conducting apparatus must have had some influence.
Thus one of these hairs answered strongly to
By these observations (which through the kindness of Herr Hensen I have myself had the opportunity of verifying) the existence of such relations as we have supposed in the case of the human cochlea, have been directly proved for these Crustaceans, and this is the more valuable, because the concealed position and ready destructibility of the corresponding organs of the human ear give little hope of our ever being able to make such a direct experiment on the intonation of its individual parts.[23]
So far the theory which has been advanced refers in the first place only to the lasting sensation produced by regular and continued periodical oscillations. But as regards the perception of irregular motions of the air, that is, of noises, it is clear that an elastic apparatus for executing vibrations could not remain at absolute rest in the presence of any force acting upon it for a time, and even a momentary motion or one recurring at irregular intervals would suffice, if only powerful enough, to set it in motion. The peculiar advantage of resonance over proper tone depends precisely on the fact that disproportionately weak individual impulses, provided that they succeed each other in correct rhythm, are capable of producing comparatively considerable motions. On the other hand, momentary but strong impulses, as for example those which result from an electric spark, will set every part of the basilar membrane into an almost equally powerful initial motion, after which each part would die off in its own proper vibrational period. By that means there might arise a simultaneous excitement of the whole of the nerves in the cochlea, which although not equally powerful would yet be proportionately gradated, and hence could not have the character of a determinate pitch. Even a weak impression on so many nerve fibres will produce a clearer impression than any single impression in itself. We know at least that small differences of brightness are more readily perceived on large than on small parts of the circle of vision, and little differences of temperature can be better perceived by plunging the whole arm, than by merely dipping a finger, into the warm water.
Hence a perception of momentary impulses by the cochlear nerves is quite possible, just as noises are perceived, without giving an especially sensible prominence to any determinate pitch.
If the pressure of the air which bears on the drumskin lasts a little longer, it will favour the motion in some regions of the basilar membrane in preference to other parts of the scale. Certain pitches will therefore be especially prominent. This we may conceive thus: every instant of pressure is considered as a pressure that will excite in every fibre of the basilar membrane a motion corresponding to itself in direction and strength and then die off; and all motions in each fibre which are thus excited are added algebraically, whence, according to circumstances, they reinforce and enfeeble each other.[24] Thus a uniform pressure which lasts during the first half vibration, that is, as long as the first positive excursion, increases the excursion of the vibrating body. But if it lasts longer it weakens the effect first produced. Hence rapidly vibrating bodies would be proportionably less excited by such a pressure, than those for which half a vibration lasts as long as, or longer than, the pressure itself. By this means such an impression would acquire a certain, though an ill-defined, pitch. In general the intensity of the sensation seems, for an equal amount of vis viva in the motion, to increase as the pitch ascends. So that the impression of the highest strongly excited fibre preponderates.
A determinate pitch, to a more remarkable extent, may also naturally result, if the pressure itself which acts on the stirrup of the drum alternates several times between positive and negative. And thus all transitional degrees between noises without any determinate pitch, and compound tones with a determinate pitch may be produced. This actually takes place, and herein lies the proof, on which Herr S. Exner[25] has properly laid weight, that such noises must be perceived by those parts of the ear which act in distinguishing pitch.
In former editions of this work I had expressed a conjecture that the auditory ciliae of the ampullae, which seemed to be but little adapted for resonance, and those of the little bags opposite the otoliths, might be especially active in the perception of noises.
As regards the ciliae in the ampullae, the investigations of Goltz have made it extremely probable that they, as well as the semicircular canals, serve for a totally different kind of sensation, namely for the perception of the turning of the head. Revolution about an axis perpendicular to the plane of one of the semicircular canals cannot be immediately transferred to the ring of water which lies in the canal, and on account of its inertia lags behind, while the relative shifting of the water along the wall of the canal might be felt by the ciliae of the nerves of the ampullae. On the other hand, if the turning continues, the ring of water itself will be gradually set in revolution by its friction against the wall of the canal, and will continue to move, even when the turning of the head suddenly ceases. This causes the elusive sensation of a revolution in the contrary direction, in the well-known form of giddiness. Injuries to the semicircular canals without injuries to the brain produce the most remarkable disturbances of equilibrium in the lower animals. Electrical discharges through the ear and cold water squirted into the ear of a person with a perforated drumskin, produce the most violent giddiness. Under these circumstances these parts of the ear can no longer with any probability be considered as belonging to the sense of hearing. Moreover impulses of the stirrup against the water of the labyrinth adjoining the oval window are in reality ill adapted for producing streams through the semicircular canals.
On the other hand the experiments of Koenig with short sounding rods, and those of Preyer with Appunn’s tuning-forks, have established the fact that very high tones with from 4000 to 40,000 vibrations in a second can be heard, but that for these the sensation of interval is extremely deficient. Even intervals of a Fifth or an Octave in the highest positions are only doubtfully recognised and are often wrongly appreciated by practised musicians. Even the major Third \(c^{\backprime}{'}\) — \(e^{\backprime}{'}\) [4096 : 5120 vibrations] was at one time heard as a Second, at another as a Fourth or a Fifth; and at still greater heights even Octaves and Fifths were confused.
If we maintain the hypothesis, that every nervous fibre hears in its own peculiar pitch, we should have to conclude that the vibrating parts of the ear which convey these sensations of the highest tones to the ear, are much less sharply defined in their capabilities of resonance, than those for deeper tones. This means that they lose any motion excited in them comparatively soon, and are also comparatively more easily brought into the state of motion necessary for sensation. This last assumption must be made, because for parts which are so strongly damped, the possibility of adding together many separate impulses is very limited, and the construction of the auditory ciliae in the little bags of the otoliths seems to me more suited for this purpose than that of the shortest fibres of the basilar membrane. If this hypothesis is confirmed we should have to regard the auditory ciliae as the bearers of squeaking, hissing, chirping, crackling sensations of sound, and to consider their reaction as differing only in degree from that of the cochlear fibres.[26]
| First Forks |
1 \(B\flat\) |
2 \(b\flat\) |
3 \(f'\) |
4 \(b'\flat\) |
5 \(d''\) |
6 \(f''\) |
7 \(a''\flat\) |
8 \(b''\flat\) |
10 | 12 | 14 | 16 | |
| Vowels |
|
f | pp | pp | |||||||||
|
|
mf | p | p | f | p | ||||||||
|
|
p | p | p | p | ff | ff | ff | ff | |||||
|
|
p | pp | p | f | f | ||||||||
|
|
p | pp | f | p | p | p | p | p | |||||
| Second Forks |
1 \(b\flat\) |
2 \(b'\flat\) |
3 \(f''\) |
4 \(b''\flat\) |
5 \(d'''\) |
6 \(f'''\) |
7 \(a'''\flat\) |
8 \(b'''\flat\) |
|||||
| Vowels |
|
f | |||||||||||
|
|
mf | f | p | ||||||||||
|
|
mf | mf | mf | f | f | ||||||||
|
|
f | f | p | ff | ff | ||||||||
|
|
mf | mf | ff | ff | ff | ||||||||
[Ueber die Grenzen der Tonwahrnehmung (On the limits of the perception of tone), June, 1876. Rearranged in English by the Translator in the Proceedings of the Musical Association, for 1876-7, pp. 1-32, under the title of 'On the Sensitiveness of the Ear to Pitch and Change of Pitch in Music'. On p. 11 of this arrangement it is stated that, including Delezenne's results,
| at vib. | a difference of | or interval of | |
| 120 | .418 vib. | 6 cents | was perceived |
| 440 | .364 '' | 1.4 '' | |
| 500 | .300 '' | 1.0 '' | |
| 1000 | .500 '' | .9 '' |
but on the other hand
| at vib. | a difference of | or interval of | |
| 60 | .200 vib. | 6 cents | was not perceived |
| 110 | .091 '' | 1.4 '' | |
| 250 | .150 '' | 1.0 '' | |
| 400 | .200 '' | .9 '' |
the intervals perceived, or not perceived, being the same, but the pitches different. And generally throughout the scale a difference of \(\tfrac15\) vib. is not heard, but
| from | \(G_{\prime}\sharp \space to \space g'\sharp \space \tfrac{2}{5} \space vib.\) | is heard |
| and from | \(a' \space to \space c'' \space \tfrac{1}{3} \space ''\) | |
| and from | \(c \space to \space c'' \space \tfrac12 \space ''\) |
— Translator.]
↵