Chapter VIII.

ON THE BEATS OF SIMPLE TONES.

We now pass to the consideration of other phenomena accompanying the simultaneous sounding of two simple tones, in which, as before, the motions of the air and of the other co-operating elastic bodies without and within the ear may be conceived as an undisturbed coexistence of two systems of vibrations corresponding to the two tones, but where the auditory sensation no longer corresponds to the sum of the two sensations which the tones would excite singly. Beats, which have now to be considered, are essentially distinguished from combinational tones as follows:— In combinational tones the composition of vibrations in the elastic vibrating bodies which are either within or without the ear, undergoes certain disturbances, although the ear resolves the motion which is finally conducted to it, into a series of simple tones, according to the usual law. In beats, on the contrary, the objective motions of the elastic bodies follow the simple law; but the composition of the sensations is disturbed. As long as several simple tones of a sufficiently different pitch enter the ear together, the sensation due to each remains undisturbed in the ear, probably because entirely different bundles of nerve fibres are affected. But tones of the same, or of nearly the same pitch, which therefore affect the same nerve fibres, do not produce a sensation which is the sum of the two they would have separately excited, but new and peculiar phenomena arise which we term interference, when caused by two perfectly equal simple tones, and beats when due to two nearly equal simple tones.

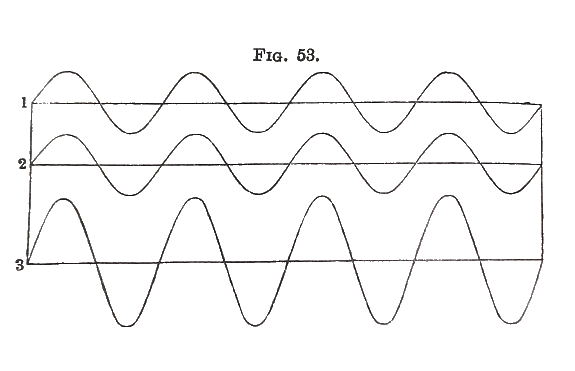
We will begin with interference. Suppose that a point in the air or ear is set in motion by some sonorous force, and that its motion is represented by the curve 1, fig. 53. Let the second motion be precisely the same at the same time and be represented by the curve 2, so that the crests of 2 fall on the crests of 1, and also the troughs of 2 on the troughs of 1. If both motions proceed at once, the whole motion will be their sum, represented by 3, a curve of the same kind but with crests twice as high and troughs twice as deep as those of either of the others. Since the intensity of sound is proportional to the square of the amplitude, we have consequently a tone not of twice but of four times the loudness of either of the others.

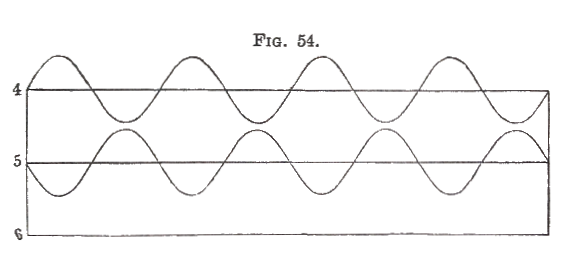
But now suppose the vibrations of the second motion to be displaced by half the periodic time. The curves to be added will stand under one another, as 4 and 5 in fig. 54, and when we come to add to them, the heights of the second curve will be still the same as those of the first, but, being, always in the contrary direction, the two will mutually destroy each other, giving as their sum the straight line 6, or no vibration at all. In this case the crests of 4 are added to the troughs of 5, and conversely, so that the crests fill up the troughs, and crests and troughs mutually annihilate each other. The intensity of sound also becomes nothing, and when motions are thus cancelled within the ear, sensation also ceases; and although each single motion acting alone would excite the corresponding auditory sensation, when both act together there is no auditory sensation at all. One sound in this case completely cancels what appears to be an equal sound. This seems extraordinarily paradoxical to ordinary contemplation because our natural consciousness apprehends sound, not as the motion of particles of the air, but as something really existing and analogous to the sensation of sound. Now as the sensation of a simple tone of the same pitch shews no oppositions of positive and negative, it naturally appears impossible for one positive sensation to cancel another. But the really cancelling things in such a case are the vibrational impulses which the two sources of sound exert on the ear. When it so happens that the vibrational impulses due to one source constantly coincide with opposite ones due to the other, and exactly counterbalance each other, no motion can possibly ensue in the ear, and hence the auditory nerve can experience no sensation.

The following are some instances of sound cancelling sound:—

Put two perfectly similar stopped organ pipes tuned to the same pitch close beside each other on the same portvent. Each one blown separately gives a powerful tone; but when they are blown together, the motion of the air in the two pipes takes place in such a manner that as the air streams out of one it streams into the other, and hence an observer at a distance hears no tone, but at most the rushing of the air. On bringing the fibre of a feather near to the lips of the pipes, this fibre will vibrate in the same way as if each pipe were blown separately. Also if a tube be conducted from the ear to the mouth of one of the pipes, the tone of that pipe is heard so much more powerfully that it cannot be entirely destroyed by the tone of the other.^[1]

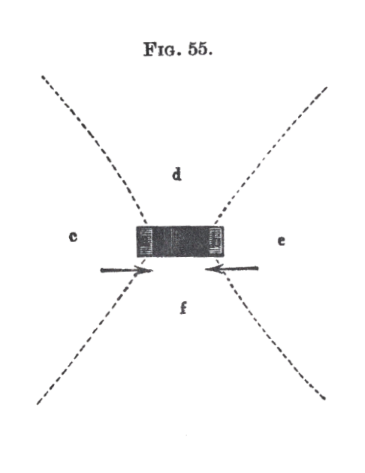
Every tuning-fork also exhibits phenomena of interference, because the prongs move in opposite directions. On striking a tuning-fork and slowly revolving it about its longitudinal axis close to the ear, it will be found that there are four positions in which the tone is heard clearly; and four intermediate positions in which it is inaudible. The four positions of strong sound are those in which either one of the prongs, or one of the side surfaces of the fork, is turned towards the ear. The positions of no sound lie between the former, almost in planes which make an angle of 45° with the surfaces of the prongs, and pass through the axis of the fork. If in fig. 55, a and b are the ends of the fork seen from above, c, d, e, f will be the four places of strong sound, and the dotted lines the four places of silence. The arrows under a and b shew the mutual motion of the two prongs. Hence while the prong a gives the air about can impulse in the direction c a, the prong b gives it an opposite one. Both impulses only partially cancel one another at c, because a acts more powerfully than b. But the dotted lines shew the places where the opposite impulses from a and b are equally strong, and consequently completely cancel each other. If the ear be brought into one of these places of silence and a narrow tube be slipped over one of the prongs a or b, taking care not to touch it, the sound will be immediately augmented, because the influence of the covered prong is almost entirely destroyed, and the uncovered prong therefore acts alone and undisturbed. ^[2]

A double siren which I have had constructed is very convenient for the demonstration of these relations. ^[3] Fig. 56 (p. 162) is a perspective view of this instrument. It is composed of two of Dove’s polyphonic sirens, of the kind previously mentioned, p. 13a; a\(_0\) and a\(_1\) are the two windchests, c\(_0\) and c\(_1\), the discs attached to a common axis, on which a screw is introduced at k, to drive a counting apparatus which can be introduced, as described on p. 12b. The upper box a, can be turned round its axis, by means of a toothed wheel, in which works a smaller wheel e provided with the driving handle d ^[4] . The axis of the box a\(_1\) round which it turns, is a prolongation of the upper pipe g\(_1\), which conducts the wind. On each of the two discs of the siren are four rows of holes, which can be either blown separately or together in any combination at pleasure, and at i are the studs for opening and closing the series of holes by a peculiar arrangement.^[5] The lower disc has four rows of 8, 10, 12, 18 holes, the upper of 9, 12, 15, 16. Hence if we call the tone of 8 holes \(c\), the lower disc gives the tones \(c\), \(e\),

\(g\), \(d'\) and the upper \(d\), \(g\), \(b\), \(c'\). We are therefore able to produce the following intervals:—

1. Unison: \(g\) \(g\) on the two discs simultaneously.

2. Octaves: \(c\) \(c'\) and \(d\) \(d\) on the two.

3. Fifths: \(c\) \(g\) and \(g\) \(d'\) either on the lower disc alone or on both discs together.

4. Fourths: \(d\) \(g\) and \(g\) \(c'\) on the upper disc alone or on both together.

5. Major Third: \(c\) \(e\) on the lower alone, and \(g\) \(b\) on the upper alone, or \(g\) \(b\) on both together.

6. Minor Third: \(e\) \(g\) on the lower, or on both together; \(b\) \(d'\) on both together.

7. Whole Tone [major Tone]: \(c\) \(d\) and \(c'\) \(d'\) on both together [the minor Tone is produced by \(d\) and \(e\) on both together].

8. Semitone [diatonic Semitone]: \(b\) \(c'\) on the upper.

When both tones are produced from the same disc the objective combinational tones are very powerful, as has been already remarked, p. 157a. But if the tones are produced from different discs, the combinational tones are weak. In the latter case (and this is the chief point of interest to us at present), the two tones can be made to act together with any desired difference of phase. This is effected by altering the position of the upper box.

We have first to investigate the phenomena as they occur in the unison \(g\) \(g\). The effect of the interference of the two tones in this case is complicated by the fact that the siren produces compound and not simple tones and that the interference of individual partial tones is independent of that of the prime tone and of one another. In order to damp the upper partial tones in the siren by means of a resonance chamber, I caused cylindrical boxes of brass to be made, of which the back halves are shewn at h\(_1\) h\(_1\) and h\(_0\) h\(_0\) fig. 56, opposite. These boxes are each made in two sections, so that they can be removed, and be again attached to the windchest by means of screws. When the tone of the siren approaches the prime tone of these boxes, its quality becomes full, strong and soft, like a fine tone on the French horn; otherwise the siren has rather a piercing tone. At the same time we use a small quantity of air, but considerable pressure. The circumstances are of the same nature as when a tongue is applied to a resonance chamber of the same pitch. Used in this way the siren is very well adapted for experiments on interference.

If the boxes are so placed that the puffs of air follow at exactly equal intervals from both discs, similar phases of the prime tone and of all partials coincide, and all are reinforced.

If the handle is turned round half a right angle, the upper box is turned round \(\small{\tfrac{1}{6}}\) of a right angle, or \(\small{\tfrac{1}{24}}\) of the circumference, that is half the distance between the holes in the series of 12 holes which is in action for \(g\). Hence the difference in the phase of the two primes is half the vibrational period, the puffs of air in one box occur exactly in the middle between those of the other, and the two prime tones mutually destroy each other. But under these circumstances the difference of phase in the upper Octave is precisely the whole of the vibrational period; that is, they reinforce each other, and similarly all the evenly numbered harmonic upper partials reinforce each other in the same position, and the unevenly numbered ones destroy each other. Hence in the new position the tone is weaker, because deprived of several of its partials; but it does not entirely cease; it rather jumps up an Octave. If we further turn the handle through another half a right angle so that the box is turned through a whole right angle, the puffs of the two discs again agree completely, and the tones reinforce one another. Hence in a complete revolution of the handle there are four positions where the whole tone of the siren appears reinforced, and four intermediate positions where the prime tone and all uneven upper partials vanish, and consequently the Octave occurs in a weaker form accompanied by the evenly numbered upper partials. If we attend to the first upper partial, which is the Octave of the prime, by listening to it through a proper resonator, we find that it vanishes after turning through a quarter of a right angle, and is reinforced after turning through half a right angle, and hence for every complete revolution of the handle it vanishes 8 times, and is reinforced 8 times. The third partial (or second upper partial), the Twelfth of the prime tone, vanishes in the same time 12 times, the fourth partial 16 times, and so on.

Other compound tones behave like those of the siren. When two tones of the same pitch are sounded together having differences of phase corresponding to half the periodic time, the tone does not vanish, but jumps up an Octave. When, for example, two open organ pipes, or two reed pipes of the same construction and pitch, are placed beside each other on the same portvent, their vibrations generally accommodate themselves in such a manner that the stream of air enters first one and then the other alternately; and while the tone of stopped pipes, which have only unevenly numbered partials, is then almost entirely destroyed, the tone of the open pipes and reed pipes falls into the upper Octave. This is the reason why no reinforcement of tone can be effected on an organ or harmonium by combining tongues or pipes of the same kind [on the same portvent].

So far we have combined tones of precisely the same pitch; now let us inquire what happens when the tones have slightly different pitch. The double siren just described is also well fitted for explaining this case, for we can slightly alter the pitch of the upper tone by slowly revolving the upper box by means of the handle, the tone becoming flatter when the direction of revolution is the same as that of the disc, and sharper when it is opposite to the same. The vibrational period of a tone of the siren is equal to the time required for a hole in the rotating disc to pass from one hole in the windbox to the next. If, through the rotation of the box, the hole of the box advances to meet the hole of the disc, the two holes come into coincidence sooner than if the box were at rest: and hence the vibrational period is shorter, and the tone sharper. The converse takes place when the revolution is in the opposite direction. These alterations of pitch are easily heard when the box is revolved rather quickly. Now produce the tones of twelve holes on both discs. These will be in absolute unison as long as the upper box is at rest. The two tones constantly reinforce or enfeeble each other according to the position of the upper box. But on setting the upper box in motion, the pitch of the upper tone is altered, while that of the lower tone, which has an immovable windbox, is unchanged. Hence we have now two tones of slightly different pitch sounding together. And we hear the so-called beats of the tones, that is, the intensity of the tone will be alternately greater and less in regular succession.^[6] The arrangement of our siren makes the reason of this readily intelligible. The revolution of the upper box brings it alternately in positions which as we have seen correspond to stronger and weaker tones. When the handle has been turned through a right angle, the windbox passes from a position of loudness through a position of weakness to a position of strength again. Consequently every complete revolution of the handle gives us four beats, whatever be the rate of revolution of the discs, and hence however low or high the tone may be. If we stop the box at the moment of maximum loudness, we continue to hear the loud tone; if at a moment of minimum force, we continue to hear the weak tone.

The mechanism of the instrument also explains the connection between the number of beats and the difference of the pitch. It is easily seen that the number of the puffs is increased by one for every quarter revolution of the handle. But every such quarter revolution corresponds to one beat. Hence the number of beats in a given time is equal to the difference of the numbers of vibrations executed by the two tones in the same time. This is the general law which determines the number of beats, for all kinds of tones. This law results immediately from the construction of the siren; in other instruments it can only be verified by very accurate and laborious measurements of the numbers of vibrations.

The intensity of tone varies; swelling from a minimum to a maximum, and lessening from the maximum to the minimum. It is the places of maximum

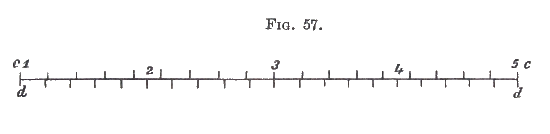
intensity which are properly called beats, and these are separated by more or less distinct pauses.

Beats are easily produced on all musical instruments, by striking two notes of nearly the same pitch. They are heard best from the simple tones of tuning-forks or stopped organ pipes, because here the tone really vanishes in the pauses. A little fluctuation in the pitch of the beating tone may then be remarked.^[7] For the compound tones of other instruments the upper partial tones are heard in the pauses, and hence the tone jumps up an Octave, as in the case of interference already described. If we have two tuning-forks of exactly the same pitch, it is only necessary to stick a little wax on to the end of one, to strike both, and bring them near the same ear or to the surface of a table, or sounding board. To make two stopped pipes beat, it is only necessary to bring a finger slowly near to the lip of one, and thus flatten it. The beats of compound tones are heard by striking any note on a pianoforte out of tune when the two strings belonging to the same note are no longer in unison; or if the piano is in tune it is sufficient to attach a piece of wax, about the size of a pea, to one of the strings. This puts them sufficiently out of tune. More attention, however, is required for compound tones because the enfeeblement of the tone is not so striking. The beat in this case resembles a fluctuation in pitch and quality. This is very striking on the siren according as the brass resonance cylinders (h\(_0\) h\(_0\) and h\(_1\) h\(_1\) of fig. 56, p. 162) are attached or not. These make the prime tone relatively strong. Hence when beats are produced by turning a handle, the decrease and increase of loudness in the tone is very striking. On removing the resonance cylinders, the upper partial tones are relatively powerful, and since the ear is very uncertain when comparing the loudness of tones of different pitch, the alteration of force during the beats is much less striking than that of pitch and quality of tone.

On listening to the upper partials of compound tones which beat, it will be found that these beat also, and that for each beat of the prime tone there are two of the second partial, three of the third and so on. Hence when the upper partials are strong, it is easy to make a mistake in counting the beats, especially when the beats of the primes are very slow, so that they occur at intervals of a second or two. It is then necessary to pay great attention to the pitch of the beats counted, and sometimes to apply a resonator.

It is possible to render beats visible by setting a suitable elastic body into sympathetic vibration with them. Beats can then occur only when the two exciting tones lie near enough to the prime tone of the sympathetic body for the latter to be set into sensible sympathetic vibration by both the tones used. This is most easily done with a thin string which is stretched on a sounding board on which have been placed two tuning-forks, both of very nearly the same pitch as the string. On observing the vibrations of the string through a microscope, or attaching a fibril of a goosefeather to the string which will make the same excursions on a magnified scale, the string will be clearly seen to make sympathetic vibrations with alternately large and small excursions, according as the tone of the two forks is at its maximum or minimum.

The same effect can be obtained from the sympathetic vibration of a stretched membrane. Fig. 58 is the copy of a drawing made by a vibrating membrane of

this sort, used in the phonautograph of Messrs. Scott & Koenig, of Paris. The membrane of this instrument, which resembles the drumskin of the ear, carries a small stiff style, which draws the vibrations of the membrane upon a rotating cylinder. In the present case the membrane was set in motion by two organ pipes, that beat. The undulating line, of which only a part is here given, shews that times of strong vibration have alternated with times of almost entire rest. In this case, then, the beats are also sympathetically executed by the membrane. Similar drawings again have been made by Dr. Politzer, who attached the writing style to the auditory bone (the columella) of a duck, and then produced a beating tone by means of two organ pipes. This experiment shewed that even the auditory bones follow the beats of two tones.^[8]

Generally this must always be the case when the pitches of the two tones struck differ so little from each other and from that of the proper tone of the sympathetic body, that the latter can be put into sensible vibration by both tones at once. Sympathetic bodies which do not damp readily, such as tuning-forks, consequently require two exciting tones which differ extraordinarily little in pitch, in order to shew visible beats, and the beats must therefore be very slow. For bodies readily damped, as membranes, strings, &c., the difference of the exciting tones may be greater, and consequently the beats may succeed each other more rapidly.

This holds also for the elastic terminal formations of the auditory nerve fibres. Just as we have seen that there may be visible beats of the auditory ossicles, Corti’s arches may also be made to beat by two tones sufficiently near in pitch to set the same Corti’s arches in sympathetic vibration at the same time. If then, as we have previously supposed, the intensity of auditory sensation in the nerve fibres involved increases and decreases with the intensity of the elastic vibrations, the strength of the sensation must also increase and diminish in the same degree as the vibrations of the corresponding elastic appendages of the nerves. In this case also the motion of Corti’s arches must still be considered as compounded of the motions which the two tones would have produced if they had acted separately. According as these motions are directed in the same or in opposite directions they will reinforce or enfeeble each other by (algebraical) addition. It is not till these motions excite sensation in the nerves that any deviation occurs from the law that each of the two tones and each of the two sensations of tones subsist side by side without disturbance.

We now come to a part of the investigation which is very important for the theory of musical consonance, and has also unfortunately been little regarded by acousticians. The question is: what becomes of the beats when they grow faster and faster? and to what extent may their number increase without the ear being unable to perceive them? Most acousticians were probably inclined to agree with the hypothesis of Thomas Young, that when the beats became very quick they gradually passed over into a combinational tone (the first differential). Young imagined that the pulses of tone which ensue during beats, might have the same effect on the ear as elementary pulses of air (in the siren, for example), and that just as 30 puffs in a second through a siren would produce the sensation of a deep tone, so would 30 beats in a second resulting from any two higher tones produce the same sensation of a deep tone. Certainly this view is well 'supported by the fact that the vibrational number of the first and strongest combinational tone is actually the number of beats produced by the two tones in a second. It is, however, of much importance to remember that there are other combinational tones (my summational tones), which will not agree with this hypothesis in any respect,^[9] but on the other hand are readily deduced from the theory of combinational tones which I have proposed (in Appendix XII.). It is moreover an objection to Young's theory, that in many cases the combinational tones exist externally to the ear, and are able to set properly tuned membranes or resonators into sympathetic vibration,^[10] because this could not possibly be the case, if the combinational tones were nothing but the series of beats with undisturbed superposition of the two waves. For the mechanical theory of sympathetic vibration shews that a motion of the air compounded of two simple vibrations of different periodic times, is capable of putting such bodies only into sympathetic vibration as have a proper tone corresponding to one of the two given tones, provided no conditions intervene by which the simple superposition of two wave systems might be disturbed; and the nature of such a disturbance was investigated in the last chapter.^[11] Hence we may consider combinational tones as an accessory phenomenon, by which, however, the course of the two primary wave systems and of their beats is not essentially interrupted.

Against the old opinion we may also adduce the testimony of our senses, which teaches us that a much greater number of beats than 30 in a second can be distinctly heard. To obtain this result we must pass gradually from the slower to the more rapid beats, taking care that the tones chosen for beating are not too far apart from each other in the scale, because audible beats are not produced unless the tones are so near to each other in the scale that they can both make the same elastic appendages of the nerves vibrate sympathetically.^[12] The number of beats, however, can be increased without increasing the interval between the tones, if both tones are taken in the higher octaves.

The observations are best begun by producing two simple tones of the same pitch, say from the once-accented octave by means of tuning-forks or stopped organ pipes, and slowly altering the pitch of one. This is effected by sticking more and more wax on one of the forks; or more and more covering the mouth of one of the pipes. Stopped organ pipes are also generally provided with a movable plug or lid at the stopped end, in order to tune them; by pulling this out we flatten, by pushing it in we sharpen the tone.^[13]

When a slight difference in pitch has been thus produced, the beats are heard at first as long drawn out fluctuations alternately swelling and vanishing. Slow beats of this kind are by no means disagreeable to the ear. In executing music containing long sustained chords, they may even produce a solemn effect, or else give a more lively, tremulous or agitating expression. Hence we find in modern organs and harmoniums, a stop with two pipes or tongues, adjusted to beat. This imitates the trembling of the human voice and of violins which, appropriately introduced in isolated passages, may certainly be very expressive and effective, but applied continuously, as is unfortunately too common, is a detestable malpractice. The ear easily follows slow beats of not more than 4 to 6 in a second. The hearer has time to apprehend all their separate phases, and become conscious of each separately, he can even count them without difficulty.^[14] But when the interval between the two tones increases to about a Semitone, the number of beats becomes 20 or 30 in a second, and the ear is consequently unable to follow them sufficiently well for counting. If, however, we begin with hearing slow beats, and then increase their rapidity more and more, we cannot fail to recognise that the sensational impression on the ear preserves precisely the same character, appearing as a series of separate pulses of sound, even when their frequency is so great that we have no longer time to fix each beat, as it passes, distinctly in our consciousness and count it.^[15]

But while the hearer in this case is quite capable of distinguishing that his ear now hears 30 beats of the same kind as the 4 or 6 in a second which he heard before, the effect of the collective impression of such a rapid beat is quite different. In the first place the mass of tone becomes confused, which I principally refer to the psychological impressions. We actually hear a series of pulses of tone, and are able to recognise it as such, although no longer capable of following each singly or separating one from the other. But besides this psychological consideration, the sensible impression is also unpleasant. Such rapidly beating tones are jarring and rough. The distinctive property of jarring, is the intermittent character of the sound. We think of the letter R as a characteristic example of a jarring tone. It is well known to be produced by interposing the uvula, or else the thin tip of the tongue, in the way of the stream of air passing out of the mouth, in such a manner as only to allow the air to force its way through in separate pulses, the consequence being that the voice at one time sounds freely, and at another is cut off.^[16]

Intermittent tones were also produced on the double siren just described by using a little reed pipe instead of the wind-conduit of the upper box, and driving the air through this reed pipe. The tone of this pipe can be heard externally only when the revolution of the disc brings its holes before the holes of the box and opens an exit for the air. Hence, if we let the disc revolve while air is driven through the pipe, we obtain an intermittent tone, which sounds exactly like beats arising from two tones sounded at once, although the intermittence is produced by purely mechanical means. Such effects may also be produced in another way on the same siren. Remove the lower windbox and retain only its pierced cover, over which the disc revolves. At the under part apply one extremity of an india-rubber tube against one of the holes in the cover, the other end being conducted by a proper ear-piece to the observer’s ear. The revolving disc alternately opens and closes the hole to which the india-rubber tube has been applied. Hold a tuning-fork in action or some other suitable musical instrument above and near the rotating disc. Its tone will be heard intermittently and the number of intermissions can be regulated by altering the velocity of the rotation of the disc.

In both ways then we obtain intermittent tones. In the first case the tone of the teed pipe as heard in the outer air is interrupted, because it can only escape from time to time. The intermittent tone in this case can be heard by any number of listeners at once. In the second case the tone in the outer air is continuous, but reaches the ear of the observer, who hears it through the disc of the siren, intermittently. It can certainly be heard by one observer only, but then all kinds of musical tones of the most diverse pitch and quality may be employed for the purpose. The intermission of their tones gives them all exactly the same kind of roughness which is produced by two tones which beat rapidly together. We thus come to recognise clearly that beats and intermissions are identical, and that either when fast enough produces what is termed a jar or rattle.

Beats produce intermittent excitement of certain auditory nerve fibres. The reason why such an intermittent excitement acts so much more unpleasantly than an equally strong or even a stronger continuous excitement, may be gathered from the analogous action of other human nerves. Any powerful excitement of a nerve deadens its excitability, and consequently renders it less sensitive to fresh irritants. But after the excitement ceases, and the nerve is left to itself, irritability is speedily re-established in a living body by the influence of arterial blood. Fatigue and refreshment apparently supervene in different organs of the body with different velocities; but they are found wherever muscles and nerves have to operate. The eye, which has in many respects the greatest analogy to the ear, is one of those organs in which both fatigue and refreshment rapidly ensue. We need to look at the sun but an instant to find that the portion of the retina, or nervous expansion of the eye, which was affected by the solar light has become less sensitive for other light. Immediately afterwards on turning our eyes to a uniformly illuminated surface, as the sky, we see a dark spot of the apparent size of the sun; or several such spots with lines between them, if we had not kept our eye steady when looking at the sun but had moved it right and left. An instant suffices to produce this effect; nay, an electric spark, that lasts an immeasurably short time, is fully capable of causing this species of fatigue.

When we continue to look at a bright surface, the impression is strongest at first, but at the same time it blunts the sensibility of the eye, and consequently the impression becomes weaker, the longer we allow the eye to act. On coming out of darkness into full daylight we feel blinded; but after a few minutes, when the sensibility of the eye has been blunted by the irritation of the light,— or, as we say, when the eye has grown accustomed to the glare,—this degree of brightness is found very pleasant. Conversely, in coming from full daylight into a dark vault, we are insensible to the weak light about us, and can scarcely find our way about, yet after a few minutes, when the eye has rested from the effect of the strong light, we are able to see very well in the semi-dark room.

These phenomena and the like can be conveniently studied in the eye, because individual spots in the eye may be excited and others left at rest, and the sensations of each may be afterwards compared. Put a piece of black paper on a tolerably well-lighted white surface, look steadily at a point on or near the black paper, and then withdraw the paper suddenly. The eye sees a secondary image of the black paper on the white surface, consisting of that portion of the white surface where the black paper lay, which now appears brighter than the rest. The place in the eye where the image of the black paper had been formed, has been rested in comparison with all those places which had been affected by the white surface, and on removing the black paper this rested part of the eye sees the white surface in its first fresh brightness, while those parts of the retina which had been already fatigued by looking at it, see a decidedly greyer tinge on the whiter surface.

Hence by the continuous uniform action of the irritation of light, this irritation itself blunts the sensibility of the nerve, and thus effectually protects this organ against too long and too violent excitement.

It is quite different when we allow intermittent light to act on the eye, such as flashes of light with intermediate pauses. During these pauses the sensibility is again somewhat re-established, and the new irritation consequently acts much more intensely than if it had lasted with the same uniform strength. Every one knows how unpleasant and annoying is any flickering light, even if it is relatively very weak, coming, for example, from a little flickering taper or rushlight.

The same thing holds for the nerves of touch. Scraping with the nail is far more annoying to the skin than constant pressure on the same place with the same pressure of the nail. The unpleasantness of scratching, rubbing, tickling, depends upon the intermittent excitement which they produce in the nerves of touch.

A jarring intermittent tone is for the nerves of hearing what a flickering light is to the nerves of sight, and scratching to the nerves of touch. A much more intense and unpleasant excitement of the organs is thus produced than would be occasioned by a continuous uniform tone. This is even shewn when we hear very weak intermittent tones. If a tuning-fork is struck and held at such a distance from the ear that its sound cannot be heard, it becomes immediately audible if the handle of the fork be revolved by the fingers. The revolution brings it alternately into positions where it can and cannot transmit sound to the ear [p. 161b], and this alternation of strength is immediately perceptible by the ear. For the same reason one of the most delicate means of hearing a very weak, simple tone consists in sounding another of nearly the same strength, which makes from 2 to 4 beats in a second with the first. In this case the strength of the tone varies from nothing to 4 times the strength of the single simple tone, and this increase of strength combines with the alternation to make it audible.

Just as this alternation of strength will serve to strengthen the impression of the very weakest musical tones upon the ear, we must conclude that it must also serve to make the impression of stronger tones much more penetrating and violent, than they would be if their loudness were continuous.

We have hitherto confined our attention to cases where the number of beats did not exceed 20 or 30 in a second. We saw that the beats in the middle part of the scale are still quite audible and form a series of separate pulses of tone. But this does not furnish a limit to their number in a second.

The interval \( b' \) \( c'' \) gave us 33 beats in a second, and the effect of sounding the two notes together was very jarring. The interval of a whole tone \( b'\flat \) \( c'' \) gives nearly twice as many beats, but these are no longer so cutting as the former. The rule assigns 88 beats in a second to the minor Third \( a' c'' \), but in reality this interval scarcely shews any of the roughness produced by beats from tones at closer intervals. We might then be led to conjecture that the increasing number of beats weakened their impression and made them inaudible. This conjecture would find an analogy in the impossibility of separating a series of rapidly succeeding impressions of light on the eye, when their number in a second is too large. Think of a glowing stick swung round in a circle. If it executes 10 or 15 revolutions in a second, the eye believes it sees a continuous circle of fire. Similarly for colour-tops, with which most of my readers are probably familiar. If the top be spun at the rate of more than 10 revolutions in a second, the colours upon it mix and form a perfectly unchanging impression of a mixed colour. It is only for very intense light that the alternations of the various fields of colour have to take place more quickly, 20 to 30 times in a second. Hence the phenomena are quite analogous for ear and eye. When the alternation between irritation and rest is too fast, the alternation ceases to be felt, and sensation becomes continuous and lasting.

However, we may convince ourselves that in the case of the ear, an increase of the number of beats in a second is not the only cause of the disappearance of the corresponding sensation. As we passed from the interval of a Semitone \( b' c'' \) to that of a minor Third \( a' c'' \), we not only increased the number of heats, but the width of the interval. Now we can increase the number of beats without increasing the interval by taking it in a higher Octave. Thus taking \( b' c'' \) an Octave higher we have \( b'' c''' \) with 66 beats, and another Octave would give us \( b''' c'''' \) with as many as 132 beats, and these are really audible in the same way as the 33 beats of \( b' c'' \), although they certainly become weaker in the higher positions. Nevertheless the 66 beats of the interval \( b'' c''' \) are much more distinct and penetrating than the same number in the whole Tone \( b'\flat c'' \), and the 88 of the interval \( e''' f''' \) are still quite evident, while the 88 of the minor Third \( a' c'' \) are practically inaudible. My assertion that as many as 132 beats in a second are audible will perhaps appear very strange and incredible to acousticians. But the experiment is easy to repeat, and if on an instrument which gives sustained tones, as an organ or harmonium, we strike a series of intervals of a Semitone each, beginning low down, and proceeding higher and higher, we shall hear in the lower parts very slow beats (\( B_1 C \) gives 4\(\small{\tfrac{1}{8}}\), \( B\) \(c \) gives 8\(\small{\tfrac{1}{4}}\), \( b c' \) gives 16\(\small{\tfrac{1}{2}}\) beats in a second), and as we ascend the rapidity will increase but the character of the sensation remain unaltered. And thus we can pass gradually from 4 to 132 beats in a second, and convince ourselves that though we become incapable of counting them, their character as a series of pulses of tone, producing an intermittent sensation, remains unaltered. It must be observed, however, that the beats, even in the higher parts of the scale, become much shriller and more distinct, when their number is diminished by taking intervals of quarter tones or less. The most penetrating roughness arises even in the upper parts of the scale from beats of 30 to 40 in a second. Hence high tones in a cord are much more sensitive to an error in tuning amounting to the fraction of a Semitone, than deep ones. While two \( c' \) notes which differ from one another by the tenth part of a Semitone, produce about 3 beats in two seconds, ^[17] which cannot be observed without considerable attention, and, at least, give no feeling of roughness, two \(c''\) notes with the same error give 3 beats in one second, and two \(c'''\) notes 6 beats in one second, which become very disagreeable. The character of the roughness also alters with the number of beats. Slow beats give a coarse kind of roughness, which may be considered as chattering or jarring; and quicker ones have a finer but more cutting roughness.

Hence it is not, or at least not solely, the large number of beats which renders them inaudible. The magnitude of the interval is a factor in the result, and consequently we are able with high tones to produce more rapid audible beats than with low tones.

Observation shews us, then, on the one hand, that equally large intervals by no means give equally distinct beats in all parts of the scale. The increasing number of beats in a second renders the beats in the upper part of the scale less distinct. The beats of a Semitone remain distinct to the upper limits of the four-times accented octave [say 4000 vib.], and this is also about the limit for musical tones fit for the combinations of harmony. The beats of a whole tone, which in deep positions are very distinct and powerful, are scarcely audible at the upper limit of the thrice-accented octave [say at 2000 vib.]. The major and minor Third, on the other hand, which in the middle of the scale [264 to 528 vib.] may be regarded as consonances, and when justly intoned scarcely shew any roughness, are decidedly rough in the lower octaves and produce distinct beats.

On the other hand we have seen that distinctness of beating and the roughness of the combined sounds do not depend solely on the number of beats. For if we could disregard their magnitudes all the following intervals, which by calculation should have 33 beats, would be equally rough:

and yet we find that these intervals are more and more free from roughness.^[18]

The roughness arising from sounding two tones together depends, then, in a compound manner on the magnitude of the interval and the number of beats produced in a second. On seeking for the reason of this dependence, we observe that, as before remarked, beats in the air can exist only when two tones are produced sufficiently near in the scale to set the same elastic appendages of the auditory nerve in sympathetic vibration at the same time. When the two tones produced are too far apart, the vibrations excited by both of them at once in Corti's organs are too weak to admit of their beats being sensibly felt, supposing of course that no upper partial or combinational tones intervene. According to the assumptions made in the last chapter respecting the degree of damping possessed by Corti’s organs (p. 144c), it would result, for example, that for the interval of a whole Tone \(c\) \(d\), such of Corti’s fibres as have the proper tone \(c\sharp\), would be excited by each of the tones with of \(\small{\tfrac{1}{10}}\) its own intensity; and these fibres will therefore fluctuate between the intensities of vibration 0 and \(\small{\tfrac{4}{10}}\). But if we strike the simple tones \(c\) and \(c\sharp\), it follows from the table there given that Corti’s fibres which correspond to the middle between \(c\) and \(c\sharp\) will alternate between the intensities 0 and \(\small{\tfrac{12}{10}}\) Conversely the same intensity of beats would for a minor Third amount to only 0.194, and for a major Third to only 0.108, and hence would be scarcely perceptible beside the two primary tones of the intensity 1. Fig. 59 (p.172), which we used on p. 144d to express the intensity of the sympathetic vibration of Corti’s fibres for an increasing interval of tone, may here serve to shew the intensity of the beats which two tones excite in the ear when forming different intervals in the scale. But the parts on the base line must now be considered to represent fifths of a whole Tone, and not as before of a Semitone. In the present case the distance of the two tones from each other is doubly as great as that between either of them and the intermediate Corti’s fibres.

Had the damping of Corti’s organs been equally great at all parts of the scale, and had the number of beats no influence on the roughness of the sensation, equal intervals in all parts of the scale would have given equal roughness to the combined tones. But as this is not the case, as the same intervals diminish in roughness as we ascend in the scale, and increase in roughness as we descend, we must either assume that the damping power of Corti’s organs of higher pitch is less than that of those of lower pitch, or else that the discrimination of the more rapid beats meets with certain hindrances in the nature of the sensation itself.

At present I see no way of deciding between these two suppositions; but the former is possibly the more improbable, because, at least with our artificial musical instruments, the higher the pitch of a vibrating body, the more difficulty is experienced in isolating it sufficiently to prevent it from communicating its vibrations to its environment. Very short, high-pitched strings, little metal tongues or plates, &c., yield high tones which die off with great rapidity, whereas it is easy to generate deep tones with correspondingly greater bodies which shall retain their tone for a considerable time. On the other hand the second supposition is favoured by the analogy of another nervous apparatus, the eye. As has been already remarked, a series of impressions of light, following each other rapidly and regularly, excite a uniform and continuous sensation of light in the eye. When the separate luminous irritations follow one another very quickly, the impression produced by each one lasts unweakened in the nerves till the next supervenes, and thus the pauses can no longer be distinguished in sensation. In the eye, the number of separate irritations cannot exceed 24 in a second without being completely fused into a single sensation. In this respect the eye is far surpassed by the ear, which can distinguish as many as 132 intermissions in a second and probably even that is not the extreme limit. Much higher tones of sufficient strength would probably allow us to hear still more.^[19] It lies in the nature of the thing, that different kinds of apparatus of sensation should shew different degrees of mobility in this respect, since the result does not depend simply on the mobility of the molecules of the nerves, but also depends upon the mobility of the auxiliary apparatus through which the excitement is induced or expressed. Muscles are much less mobile than the eye; ten electrical discharges in a second directed through them generally suffice to bring the voluntary muscles into a permanent state of contraction. For the muscles of the involuntary system, of the bowels, the vessels, &c., the pauses between the irritations may be as much as one, or even several seconds long, without any intermission in the continuity of contraction.

The ear is greatly superior in this respect to any other nervous apparatus. It is eminently the organ for small intervals of time, and has been long used as such by astronomers. It is well known that when two pendulums are ticking near one another, the ear can distinguish whether the ticks are or are not coincident, within one hundredth of a second. The eye would certainly fail to determine whether two flashes of light coincided within \(\small{\tfrac{1}{24}}\) second; and probably within a much larger fraction of a second.^[20]

But although the ear shews its superiority over other organs of the body in this respect, we cannot hesitate to assume that, like every other nervous apparatus, the rapidity of its power of apprehension is limited, and we may even assume that we have approached very near the limit when we can but faintly distinguish 132 beats in a second.