Sensations result from the action of an external stimulus on the sensitive apparatus of our nerves. Sensations differ in kind, partly with the organ of sense excited, and partly with the nature of the stimulus employed. Each organ of sense produces peculiar sensations, which cannot be excited by means of any other; the eye gives sensations of light, the ear sensations of sound, the skin sensations of touch. Even when the same sunbeams which excite in the eye sensations of light, impinge on the skin and excite its nerves, they are felt only as heat, not as light. In the same way the vibration of elastic bodies heard by the ear, can also be felt by the skin, but in that case produce only a whirring fluttering sensation, not sound. The sensation of sound is therefore a species of reaction against external stimulus, peculiar to the ear, and excitable in no other organ of the body, and is completely distinct from the sensation of any other sense.

As our problem is to study the laws of the sensation of hearing, our first business will be to examine how many kinds of sensation the ear can generate, and what differences in the external means of excitement or sound, correspond to these differences of sensation.

The first and principal difference between various sounds experienced by our ear, is that between noises and musical tones. The soughing, howling, and whistling of the wind, the splashing of water, the rolling and rumbling of carriages, are examples of the first kind, and the tones of all musical instruments of the second. Noises and musical tones may certainly intermingle in very various degrees, and pass insensibly into one another, but their extremes are widely separated.

The nature of the difference between musical tones and noises, can generally be determined by attentive aural observation without artificial assistance. We perceive that generally, a noise is accompanied by a rapid alternation of different kinds of sensations of sound. Think, for example, of the rattling of a carriage over granite paving stones, the splashing or seething of a waterfall or of the waves of the sea, the rustling of leaves in a wood. In all these cases we have rapid, irregular, but distinctly perceptible alternations of various kinds of sounds, which crop up fitfully. When the wind howls the alternation is slow, the sound slowly and gradually rises and then falls again. It is also more or less possible to separate restlessly alternating sounds in case of the greater number of other noises. We shall hereafter become acquainted with an instrument, called a resonator, which will materially assist the ear in making this separation. On the other hand, a musical tone strikes the ear as a perfectly undisturbed, uniform sound which remains unaltered as long as it exists, and it presents no alternation of various kinds of constituents. To this then corresponds a simple, regular kind of sensation, whereas in a noise many various sensations of musical tone are irregularly mixed up and as it were tumbled about in confusion. We can easily compound noises out of musical tones, as, for example, by simultaneously striking all the keys contained in one or two octaves of a pianoforte. This shews us that musical tones are the simpler and more regular elements of the sensations of hearing, and that we have consequently first to study the laws and peculiarities of this class of sensations.

Then comes the further question: On what difference in the external means of excitement does the difference between noise and musical tone depend? The normal and usual means of excitement for the human ear is atmospheric vibration. The irregularly alternating sensation of the ear in the case of noises leads us to conclude that for these the vibration of the air must also change irregularly. For musical tones on the other hand we anticipate a regular motion of the air, continuing uniformly, and in its turn excited by an equally regular motion of the sonorous body, whose impulses were conducted to the ear by the air.

Those regular motions which produce musical tones have been exactly investigated by physicists. They are oscillations, vibrations, or swings, that is, up and down, or to and fro motions of sonorous bodies, and it is necessary that these oscillations should be regularly periodic. By a periodic motion we mean one which constantly returns to the same condition after exactly equal intervals of time. The length of the equal intervals of time between one state of the motion and its next exact repetition, we call the length of the oscillation, vibration, or swing, or the period of the motion. In what manner the moving body actually moves during one period, is perfectly indifferent. As illustrations of periodical motion, take the motion of a clock pendulum, of a stone attached to a string and whirled round in a circle with uniform velocity, of a hammer made to rise and fall uniformly by its connection with a water wheel. All these motions, however different be their form, are periodic in the sense here explained. The length of their periods, which in the cases adduced is generally from one to several seconds, is relatively long in comparison with the much shorter periods of the vibrations producing musical tones, the lowest or deepest of which makes at least 30 in a second, while in other cases their number may increase to several thousand in a second.

Our definition of periodic motion then enables us to answer the question proposed as follows: — The sensation of a musical tone is due to a rapid periodic motion of the sonorous body; the sensation of a noise to non-periodic motions.

The musical vibrations of solid bodies are often visible. Although they may be too rapid for the eye to follow them singly, we easily recognise that a sounding string, or tuning-fork, or the tongue of a reed-pipe, is rapidly vibrating between two fixed limits, and the regular, apparently immovable image that we see, notwithstanding the real motion of the body, leads us to conclude that the backward and forward motions are quite regular. In other cases we can feel the swinging motions of sonorous solids. Thus, the player feels the trembling of the reed in the mouthpiece of a clarinet, oboe, or bassoon, or of his own lips in the mouthpieces of trumpets and trombones.

The motions proceeding from the sounding bodies are usually conducted to our ear by means of the atmosphere. The particles of air must also execute periodically recurrent vibrations, in order to excite the sensation of a musical tone in our ear. This is actually the case, although in daily experience sound at first seems to be some agent, which is constantly advancing through the air, and propagating itself further and further. We must, however, here distinguish between the motion of the individual particles of air — which takes place periodically backwards and forwards within very narrow limits — and the propagation of the sonorous tremor. The latter is constantly advancing by the constant attraction of fresh particles into its sphere of tremor.

This is a peculiarity of all so-called undulatory motions. Suppose a stone to be thrown into a piece of calm water. Round the spot struck there forms a little ring of wave, which, advancing equally in all directions, expands to a constantly increasing circle. Corresponding to this ring of wave, sound also proceeds in the air from the excited point and advances in all directions as far as the limits of the mass of air extend. The process in the air is essentially identical with that on the surface of the water. The principal difference consists in the spherical propagation of sound in all directions through the atmosphere which fills all surrounding space, whereas the waves of the water can only advance in rings or circles on its surface. The crests of the waves of water correspond in the waves of sound to spherical shells where the air is condensed, and the troughs to shells where it is rarefied. On the free surface of the water, the mass when compressed can slip upwards and so form ridges, but in the interior of the sea of air, the mass must be condensed, as there is no unoccupied spot for its escape.

The waves of water, therefore, continually advance without returning. But we must not suppose that the particles of water of which the waves are composed advance in a similar manner to the waves themselves. The motion of the particles of water on the surface can easily be rendered visible by floating a chip of wood upon it. This will exactly share the motion of the adjacent particles. Now, such a chip is not carried on by the rings of wave. It only bobs up and down and finally rests on its original spot. The adjacent particles of water move in the same manner. When the ring of wave reaches them they are set bobbing; when it has passed over them they are still in their old place, and remain there at rest, while the ring of wave continues to advance towards fresh spots on the surface of the water, and sets new particles of water in motion. Hence the waves which pass over the surface of the water are constantly built up of fresh particles of water. What really advances as a wave is only the tremor, the altered form of the surface, while the individual particles of water themselves merely move up and down transiently, and never depart far from their original position.

The same relation is seen still more clearly in the waves of a rope or chain. Take a flexible string of several feet in length, or a thin metal chain, hold it at one end and let the other hang down, stretched by its own weight alone. Now, move the hand by which you hold it quickly to one side and back again. The excursion which we have caused in the upper end of the string by moving the hand, will run down it as a kind of wave, so that constantly lower parts of the string will make a sidewards excursion while the upper return again into the straight position of rest. But it is evident that while the wave runs down, each individual particle of the string can have only moved horizontally backwards and forwards, and can have taken no share at all in the advance of the wave.

The experiment succeeds still better with a long elastic line, such as a thick piece of india-rubber tubing, or a brass-wire spiral spring, from eight to twelve feet in length, fastened at one end, and slightly stretched by being held with the hand at the other. The hand is then easily able to excite waves which will run very regularly to the other end of the line, be there reflected and return. In this case it is also evident that it can be no part of the line itself which runs backwards and forwards, but that the advancing wave is composed of continually fresh particles of the line. By these examples the reader will be able to form a mental image of the kind of motion to which sound belongs, where the material particles of the body merely make periodical oscillations, while the tremor itself is constantly propagated forwards.

Now let us return to the surface of the water. We have supposed that one of its points has been struck by a stone and set in motion. This motion has spread out in the form of a ring of wave over the surface of the water, and having reached the chip of wood has set it bobbing up and down. Hence by means of the wave, the motion which the stone first excited in one point of the surface of the water has been communicated to the chip which was at another point of the same surface. The process which goes on in the atmospheric ocean about us, is of a precisely similar nature. For the stone substitute a sounding body, which shakes the air; for the chip of wood substitute the human ear, on which impinge the waves of air excited by the shock, setting its movable parts in vibration. The waves of air proceeding from a sounding body, transport the tremor to the human ear exactly in the same way as the water transports the tremor produced by the stone to the floating chip.

In this way also it is easy to see how a body which itself makes periodical oscillations, will necessarily set the particles of air in periodical motion. A falling stone gives the surface of the water a single shock. Now replace the stone by a regular series of drops falling from a vessel with a small orifice. Every separate drop will excite a ring of wave, each ring of wave will advance over the surface of the water precisely like its predecessor, and will be in the same way followed by its successors. In this manner a regular series of concentric rings will be formed and propagated over the surface of the water. The number of drops which fall into the water in a second will be the number of waves which reach our floating chip in a second, and the number of times that this chip will therefore bob up and down in a second, thus executing a periodical motion, the period of which is equal to the interval of time between the falling of consecutive drops. In the same way for the atmosphere, a periodically oscillating sonorous body produces a similar periodical motion, first in the mass of air, and then in the drumskin of our ear, and the period of these vibrations must be the same as that of the vibration in the sonorous body.

Having thus spoken of the principal division of sound into Noise and Musical Tones, and then described the general motion of the air for these tones, we pass on to the peculiarities which distinguish such tones one from the other. We are acquainted with three points of difference in musical tones, confining our attention in the first place to such tones as are isolatedly produced by our usual musical instruments, and excluding the simultaneous sounding of the tones of different instruments. Musical tones are distinguished: —

1. By their force,
2. By their pitch,
3. By their quality.

It is unnecessary to explain what we mean by the force and pitch of a tone. By the quality of a tone we mean that peculiarity which distinguishes the musical tone of a violin from that of a flute or that of a clarinet, or that of the human voice, when all these instruments produce the same note at the same pitch.

We have now to explain what peculiarities of the motion of sound correspond to these three principal differences between musical tones.

First, We easily recognise that the force of a musical tone increases and diminishes with the extent or so-called amplitude of the oscillations of the particles of the sounding body. When we strike a string, its vibrations are at first sufficiently large for us to see them, and its corresponding tone is loudest. The visible vibrations become smaller and smaller, and at the same time the loudness diminishes. The same observation can be made on strings excited by a violin bow, and on the reeds of reed-pipes, and on many other sonorous bodies. The same conclusion results from the diminution of the loudness of a tone when we increase our distance from the sounding body in the open air, although the pitch and quality remain unaltered; for it is only the amplitude of the oscillations of the particles of air which diminishes as their distance from the sounding body increases. Hence loudness must depend on this amplitude, and none other of the properties of sound do so.^[1]

The second essential difference between different musical tones consists in their pitch. Daily experience shews us that musical tones of the same pitch can be produced upon most diverse instruments by means of most diverse mechanical contrivances, and with most diverse degrees of loudness. All the motions of the air thus excited must be periodic, because they would not otherwise excite in us the sensation of a musical tone. But the sort of motion within each single period may be any whatever, and yet if the length of the periodic time of two musical tones is the same, they have the same pitch. Hence: Pitch depends solely on the length of time in which each single vibration is executed, or, which comes to the same thing, on the number of vibrations completed in a given time. We are accustomed to take a second as the unit of time, and shall consequently mean by the pitch number [or frequency] of a tone, the number of vibrations which the particles of a sounding body perform in one second of time.^[2] It is self-evident that we find the periodic time or vibrational period, that is length of time which is occupied in performing a single vibration backwards and forwards, by dividing one second of time by the pitch number.

Musical tones are said to be higher, the greater their pitch numbers, that is, the shorter their vibrational periods.

The exact determination of the pitch number for such elastic bodies as produce audible tones, presents considerable difficulty, and physicists had to contrive many comparatively complicated processes in order to solve this problem for each particular case. Mathematical theory and numerous experiments had to render mutual assistance.^[3] It is consequently very convenient for the demonstration of the fundamental facts in this department of knowledge, to be able to apply a peculiar instrument for producing musical tones — the so-called siren — which is constructed in such a manner as to determine the pitch number of the tone produced, by a direct observation. The principal parts of the simplest form of the siren are shewn in fig. 1, after Seebeck.

A is a thin disc of cardboard or tinplate, which can be set in rapid rotation about its axle b by means of a string f f, which passes over a larger wheel. On the margin of the disc there is punched a set of holes at equal intervals: of these there are twelve in the figure; one or more similar series of holes at equal distances are introduced on concentric circles (there is one such of eight holes in the figure), c is a pipe which is directed over one of the holes. Now, on setting the disc in rotation and blowing through the pipe c, the air will pass freely whenever one of the holes comes under the end of the pipe, but will be checked whenever an unpierced portion of the disc comes under it. Each hole of the disc, then, that passes the end of the pipe lets a single puff of air escape. Supposing the disc to make a single revolution and the pipe to be directed to the outer circle of holes, we have twelve puffs corresponding to the twelve holes; but if the pipe is directed to the inner circle we have only eight puffs. If the disc is made to revolve ten times in one second, the outer circle will produce 120 puffs in one second, which would give rise to a weak and deep musical tone, and the inner circle eighty puffs. Generally, if we know the number of revolutions which the disc makes in a second, and the number of holes in the series to which the tube is directed, the product of these two numbers evidently gives the number of puffs in a second. This number is consequently far easier to determine exactly than in any other musical instrument, and sirens are accordingly extremely well adapted for studying all changes in musical tones resulting from the alterations and ratios of the pitch numbers.

The form of siren here described gives only a weak tone. I have placed it first because its action can be most readily understood, and, by changing the disc, it can be easily applied to experiments of very different descriptions. A stronger tone is produced in the siren of Cagniard de la Tour, shewn in figures 2, 3, and 4, above. Here s s is the rotating disc, of which the upper surface is shewn in fig. 3, and the side is seen in figs. 2 and 4. It is placed over a windchest A A, which is connected with a bellows by the pipe B B. The cover of the windchest A A, which lies immediately under the rotating disc s s, is pierced with precisely the same number of holes as the disc, and the direction of the holes pierced in the cover of the chest is oblique to that of the holes in the disc, as shewn in fig. 4, which is a vertical section of the instrument through the line n n in fig. 3. This position of the holes enables the wind escaping from A A to set the disc s s in rotation, and by increasing the pressure of the bellows, as much as 50 or 60 rotations in a second can be produced. Since all the holes of one circle are blown through at the same time in this siren, a much more powerful tone is produced than in Seebeck's, fig. 1 (p. 11). To record the revolutions, a counter z z introduced, connected with a toothed wheel which works in the screw t, and advances one tooth for each revolution of the disc s s. By the handle h this counter may be moved slightly to one side, so that the wheelwork and screw may be connected or disconnected at pleasure. If they are connected at the beginning of one second, and disconnected at the beginning of another, the hand of the counter shews how many revolutions of the disc have been made in the corresponding number of seconds.^[4]

Dove ^[5] introduced into this siren several rows of holes through which the wind might be directed, or from which it might be cut off, at pleasure. A polyphonic siren of this description with other peculiar arrangements will be figured and described in Chapter VIII., fig. 56.

It is clear that when the pierced disc of one of these sirens is made to revolve with a uniform velocity, and the air escapes through the holes in puffs, the motion of the air thus produced must be periodic in the sense already explained. The holes stand at equal intervals of space, and hence on rotation follow each other at equal intervals of time. Through every hole there is poured, as it were, a drop of air into the external atmospheric ocean, exciting waves in it, which succeed each other at uniform intervals of time, just as was the case when regularly falling drops impinged upon a surface of water (p. 10). Within each separate period, each individual puff will have considerable variations of form in sirens of different construction, depending on the different diameters of the holes, their distance from each other, and the shape of the extremity of the pipe which conveys the air; but in every case, as long as the velocity of rotation and the position of the pipe remain unaltered, a regularly periodic motion of the air must result, and consequently the sensation of a musical tone must be excited in the ear, and this is actually the case.

It results immediately from experiments with the siren that two series of the same number of holes revolving with the same velocity, give musical tones of the same pitch, quite independently of the size and form of the holes, or of the pipe. We even obtain a musical tone of the same pitch if we allow a metal point to strike in the holes as they revolve instead of blowing. Hence it follows firstly that the pitch of a tone depends only on the number of puffs or swings, and not on their form, force, or method of production. Further it is very easily seen with this instrument that on increasing the velocity of rotation and consequently the number of puffs produced in a second, the pitch becomes sharper or higher. The same result ensues if, maintaining a uniform velocity of rotation, we first blow into a series with a smaller and then into a series with a greater number of holes. The latter gives the sharper or higher pitch.

With the same instrument we also very easily find the remarkable relation which the pitch numbers of two musical tones must possess in order to form a consonant interval. Take a series of 8 and another of 16 holes in a disc, and blow into both sets while the disc is kept at uniform velocity of rotation. Two tones will be heard which stand to one another in the exact relation of an Octave. Increase the velocity of rotation; both tones will become sharper, but both will continue at the new pitch to form the interval of an Octave. ^[6] Hence we conclude that a musical tone which is an Octave higher than another, makes exactly twice as many vibrations in a given time as the latter.

The disc shewn in fig. 1, p. 11, has two circles of 8 and 12 holes respectively. Each, blown successively, gives two tones which form with each other a perfect Fifth, independently of the velocity of rotation of the disc. Hence, two musical tones stand in the relation of a so-called Fifth when the higher tone makes three vibrations in the same time as the lower makes two.

If we obtain a musical tone by blowing into a circle of 8 holes, we require a circle of 16 holes for its Octave, and 12 for its Fifth. Hence the ratio of the pitch numbers of the Fifth and the Octave is 12 : 16 or 3 : 4. But the interval between the Fifth and the Octave is the Fourth, so that we see that when two musical tones form a Fourth, the higher makes four vibrations while the lower makes three.

The polyphonic siren of Dove has usually four circles of 8, 10, 12 and 16 holes respectively. The series of 16 holes gives the Octave of the series of 8 holes, and the Fourth of the series of 12 holes. The series of 12 holes gives the Fifth of the series of 8 holes, and the minor Third of the series of 10 holes. While the series of 10 holes gives the major Third of the series of 8 holes. The four series consequently give the constituent musical tones of a major chord.

By these and similar experiments we find the following relations of the pitch numbers: —

When the fundamental tone of a given interval is taken an Octave higher, the interval is said to be inverted. Thus a Fourth is an inverted Fifth, a minor Sixth an inverted major Third, and a major Sixth an inverted minor Third. The corresponding ratios of the pitch numbers are consequently obtained by doubling the smaller number in the original interval.

These are all the consonant intervals which lie within the compass of an Octave. With the exception of the minor Sixth, which is really the most imperfect of the above consonances, the ratios of their vibrational numbers are all expressed by means of the whole numbers, 1, 2, 3, 4, 5, 6.

Comparatively simple and easy experiments with the siren, therefore, corroborate that remarkable law mentioned in the Introduction (p. 1), according to which the pitch numbers of consonant musical tones bear to each other ratios expressible by small whole numbers. In the course of our investigation we shall employ the same instrument to verify more completely the strictness and exactness of this law.

Long before anything was known of pitch numbers, or the means of counting them, Pythagoras had discovered that if a string be divided into two parts by a bridge, in such a way as to give two consonant musical tones when struck, the lengths of these parts must be in the ratio of these whole numbers. If the bridge is so placed that \(\small{\tfrac23}\) of the string lie to the right, and \(\small{\tfrac13}\) on the left, so that the two lengths are in the ratio of 2 : 1, they produce the interval of an Octave, the greater length giving the deeper tone. Placing the bridge so that \(\small{\tfrac35}\) of the string lie on the right and \(\small{\tfrac25}\) on the left, the ratio of the two lengths is 3 : 2, and the interval is a Fifth.

These measurements had been executed with great precision by the Greek musicians, and had given rise to a system of tones, contrived with considerable art. For these measurements they used a peculiar instrument, the monochord, consisting of a sounding board and box on which a single string was stretched with a scale below, so as to set the bridge correctly.^[7]

It was not till much later that, through the investigations of Galileo (1638), Newton, Euler (1729), and Daniel Bernouilli (1771), the law governing the motions of strings became known, and it was thus found that the simple ratios of the lengths of the strings existed also for the pitch numbers of the tones they produced, and that they consequently belonged to the musical intervals of the tones of all instruments, and were not confined to the lengths of strings through which the law had been first discovered.

This relation of whole numbers to musical consonances was from all time looked upon as a wonderful mystery of deep significance. The Pythagoreans themselves made use of it in their speculations on the harmony of the spheres. From that time it remained partly the goal and partly the starting point of the strangest and most venturesome, fantastic or philosophic combinations, till in modern times the majority of investigators adopted the notion accepted by Euler himself, that the human mind had a peculiar pleasure in simple ratios, because it could better understand them and comprehend their bearings. But it remained uninvestigated how the mind of a listener not versed in physics, who perhaps was not even aware that musical tones depended on periodical vibrations, contrived to recognise and compare these ratios of the pitch numbers. To shew what processes taking place in the ear, render sensible the difference between consonance and dissonance, will be one of the principal problems in the second part of this work.

By means of the ratios of the pitch numbers already assigned for the consonant intervals, it is easy, by pursuing these intervals throughout, to calculate the ratios for the whole extent of the musical scale.

The major triad or chord of three tones, consists of a major Third and a Fifth. Hence its ratios are:

If we associate with this triad that of its dominant \(G : B : D\), and that of its sub-dominant \(F : A : C\), each of which has one tone in common with the triad of the tonic \(C : E : G\), we obtain the complete series of tones for the major scale of \(C\), with the following ratio of the pitch numbers:

In order to extend the calculation to other octaves, we shall adopt the following notation of musical tones, marking the higher octaves by accents, as is usual in Germany, ^[8] as follows:

1. The unaccented or small octave (the 4-foot octave on the organ^[9]): —

2. The once-accented octave (2-foot) : —

3. The twice-accented octave (1-foot) : —

And so on for higher octaves. Below the small octave lies the great octave, written with unaccented capital letters; its \(C\) requires an organ pipe of eight feet in length, and hence it is called the 8-foot octave.

4. Great or 8-foot octave : —

Below this follows the 16-foot or contra-octave; the lowest on the pianoforte and most organs, the tones of which may be represented by \(C_{\prime} \; D_{\prime} \; E_{\prime} \; F_{\prime} \; G_{\prime} \; A_{\prime} \; B_{\prime}\), with an inverted accent. On great organs there is a still deeper, 32-foot octave, the tones of which may be written \(C_{\prime\prime} \; D_{\prime\prime} \; E_{\prime\prime} \; F_{\prime\prime} \; G_{\prime\prime} \; A_{\prime\prime} \; B_{\prime\prime}\), with two inverted accents, but they scarcely retain the character of musical tones. (See Chap. IX.)

Since the pitch numbers of any octave are always twice as great as those for the next deeper, we find the pitch numbers of the higher tones by multiplying those of the small or unaccented octave as many times by 2 as its symbol has upper accents. And on the contrary the pitch numbers for the deeper octaves are found by dividing those of the great octave, as often as its symbol has lower accents.

For the pitch of the musical scale German physicists have generally adopted that proposed by Scheibler, and adopted subsequently by the German Association of Natural Philosophers (die deutsche Naturforscherversammlung) in 1834. This makes the once-accented \(a'\) execute 440 vibrations in a second.^[10] Hence results the following table for the scale of \(C\) major, which will serve to determine the pitch of all tones that are defined by their pitch numbers in the following work.

The lowest tone on orchestral instruments is the \(E_{\prime}\) of the double bass, making 41\(\tfrac14\) vibrations in a second. ^[12] Modern pianofortes and organs usually go down to C, with 33 vibrations, and the latest grand pianos even down to \(A_{\prime\prime}\) with 27\(\tfrac12\) vibrations. On larger organs, as already mentioned, there is also a deeper Octave reaching to \(C_{\prime\prime}\) with 16\(\tfrac12\) vibrations. But the musical character of all these tones below is imperfect, because we are here near to the limit of the power of the ear to combine vibrations into musical tones. These lower tones cannot therefore be used musically except in connection with their higher octaves to which they impart a character of greater depth without rendering the conception of the pitch indeterminate.

Upwards, pianofortes generally reach \(a''''\) with 3520, or even \(c^{\text{v}}\) with 4224 vibrations. The highest tone in the orchestra is probably the five-times accented \(d^{\text{v}}\) of the piccolo flute with 4752 vibrations. Appunn and W. Preyer by means of small tuning-forks excited by a violin bow have even reached the eight times accented \(e^{\text{viii}}\) with 40,960 vibrations in a second. These high tones were very painfully unpleasant, and the pitch of those which exceed the boundaries of the musical scale was very imperfectly discriminated by musical observers.^[13] More on this in Chap. IX.

The musical tones which can be used with advantage, and have clearly distinguishable pitch, have therefore between 40 and 4000 vibrations in a second, extending over 7 octaves. Those which are audible at all have from 20 to 40,000 vibrations, extending over about 11 octaves. This shews what a great variety of different pitch numbers can be perceived and distinguished by the ear. In this respect the ear is far superior to the eye, which likewise distinguishes light of different periods of vibration by the sensation of different colours, for the compass of the vibrations of light distinguishable by the eye but slightly exceeds an Octave. ^[14]

Force and pitch were the two first differences which we found between musical tones; the third was quality of tone, which we have now to investigate. When we hear notes of the same force and same pitch sounded successively on a pianoforte, a violin, clarinet, oboe, or trumpet, or by the human voice, the character of the musical tone of each of these instruments, notwithstanding the identity of force and pitch, is so different that by means of it we recognise with the greatest ease which of these instruments was used. Varieties of quality of tone appear to be infinitely numerous. Not only do we know a long series of musical instruments which could each produce a note of the same pitch; not only do different individual instruments of the same species, and the voices of different individual singers shew certain more delicate shades of quality of tone, which our ear is able to distinguish; but notes of the same pitch can sometimes be sounded on the same instrument with several qualitative varieties. In this respect the 'bowed' instruments (i.e. those of the violin kind) are distinguished above all other. But the human voice is still richer, and human speech employs these very qualitative varieties of tone, in order to distinguish different letters. The different vowels, namely, belong to the class of sustained tones which can be used in music, while the character of consonants mainly depends upon brief and transient noises.

On inquiring to what external physical difference in the waves of sound the different qualities of tone correspond, we must remember that the amplitude of the vibration determines the force or loudness, and the period of vibration the pitch. Quality of tone can therefore depend upon neither of these. The only possible hypothesis, therefore, is that the quality of tone should depend upon the manner in which the motion is performed within the period of each single vibration. For the generation of a musical tone we have only required that the motion should be periodic, that is, that in any one single period of vibration exactly the same state should occur, in the same order of occurrence as it presents itself in any other single period. As to the kind of motion that should take place within any single period, no hypothesis was made. In this respect then an endless variety of motions might be possible for the production of sound.

Observe instances, taking first such periodic motions as are performed so slowly that we can follow them with the eye. Take a pendulum, which we can at any time construct by attaching a weight to a thread and setting it in motion. The pendulum swings from right to left with a uniform motion, uninterrupted by jerks. Near to either end of its path it moves slowly, and in the middle fast. Among sonorous bodies, which move in the same way, only very much faster, we may mention tuning-forks. When a tuning-fork is struck or is excited by a violin bow, and its motion is allowed to die away slowly, its two prongs oscillate backwards and forwards in the same way and after the same law as a pendulum, only they make many hundred swings for each single swing of the pendulum.

As another example of a periodic motion, take a hammer moved by a waterwheel. It is slowly raised by the millwork, then released, and falls down suddenly, is then again slowly raised, and so on. Here again we have a periodical backwards and forwards motion; but it is manifest that this kind of motion is totally different from that of the pendulum. Among motions which produce musical sounds, that of a violin string, excited by a bow, would most nearly correspond with the hammer's, as will be seen from the detailed description in Chap. V. The string clings for a time to the bow, and is carried along by it, then suddenly releases itself, like the hammer in the mill, and, like the latter, retreats somewhat with much greater velocity than it advanced, and is again caught by the bow and carried forward.

Again, imagine a ball thrown up vertically, and caught on its descent with a blow which sends it up again to the same height, and suppose this operation to be performed at equal intervals of time. Such a ball would occupy the same time in rising as in falling, but at the lowest point its motion would be suddenly interrupted, whereas at the top it would pass through gradually diminishing speed of ascent into a gradually increasing speed of descent. This then would be a third kind of alternating periodic motion, and would take place in a manner essentially different from the other two.

To render the law of such motions more comprehensible to the eye than is possible by lengthy verbal descriptions, mathematicians and physicists are in the habit of applying a graphical method, which must be frequently employed in this work, and should therefore be well understood.

To render this method intelligible suppose a drawing point b, fig. 5, to be fastened to the prong A of a tuning-fork in such a manner as to mark a surface of paper B B. Let the tuning-fork be moved with a uniform velocity in the direction of the upper arrow, or else the paper be drawn under it in the opposite direction, as shewn by the lower arrow. When the fork is not sounding, the point will describe the dotted straight line d c. But if the prongs have been first set in vibration, the point will describe the undulating line d c, for as the prong vibrates, the attached point b will constantly move backwards and forwards, and hence be

sometimes on the right and sometimes on the left of the dotted straight line d c, as is shewn by the wavy line in the figure. This wavy line, once drawn, remains as a permanent image of the kind of motion performed by the end of the fork during its musical vibrations. As the point b is moved in the direction of the straight line d c with a constant velocity, equal sections of the straight line d c will correspond to equal sections of the time during which the motion lasts, and the distance of the wavy line on either side of the straight line will shew how far the point b has moved from its mean position to one side or the other during those sections of time.

In actually performing such an experiment as this, it is best to wrap the paper over a cylinder which is made to rotate uniformly by clockwork. The paper is wetted, and then passed over a turpentine flame which coats it with lampblack, on which a fine and somewhat smooth steel point will easily trace delicate lines.

Fig. 6 is the copy of a drawing actually made in this way on the rotating cylinder of Messrs. Scott and Koenig's Phonautograph.

Fig. 7 shews a portion of this curve on a larger scale. It is easy to see the meaning of such a curve. The drawing point has passed with a uniform velocity in the direction e h. Suppose that it has described the section e g in \(\tfrac{1}{10}\) of a second. Divide e g into 12 equal parts, as in the figure, then the point has been \(\tfrac{1}{120}\) of a second in describing the length of any such section horizontally, and the curve shews us on what side and at what distance from the position of rest the vibrating point will be at the end of \(\tfrac{1}{120}\), \(\tfrac{2}{120}\), and so on, of a second, or, generally, at any given short interval of time since it left the point e. We see, in the figure, that after of \(\tfrac{1}{120}\) a second it had reached the height 1, and that it rose gradually till the end of \(\tfrac{3}{120}\) of a second; then, however, it began to descend gradually till, at the end of \(\tfrac{6}{120}=\tfrac{1}{20}\) seconds, it had reached its mean position f, and then it continued descending on the opposite side till the end of \(\tfrac{9}{120}\) of a second and so on. We can also easily determine where the vibrating point was to be found at the end of any fraction of this hundred-and-twentieth of a second. A drawing of this kind consequently shews immediately at what point of its path a vibrating particle is to be found at any given instant, and hence gives a complete image of its motion. If the reader wishes to reproduce the motion of the vibrating point, he has only to cut a narrow vertical slit in a piece of paper, and place it over fig. 6 or fig. 7, so as to shew a very small portion of the curve through the vertical slit, and draw the book slowly but uniformly under the slit, from right to left; the white or black point in the slit will then appear to move backwards and forwards in precisely the same manner as the original drawing point attached to the fork, only of course much more slowly.

We are not yet able to make all vibrating bodies describe their vibrations

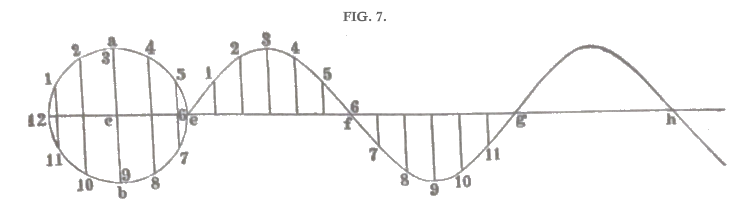
directly on paper, although much progress has recently been made in the methods required for this purpose. But we are able ourselves to draw such curves for all sounding bodies, when the law of their motion is known, that is, when we know how far the vibrating point will be from its mean position at any given moment of time. We then set off on a horizontal line, such as e f, fig. 7, lengths corresponding to the interval of time, and let fall perpendiculars to it on either side, making their lengths equal or proportional to the distance of the vibrating point from its mean position, and then by joining the extremities of these perpendiculars we obtain a curve such as the vibrating body would have drawn if it had been possible to make it do so.

Thus fig. 8 represents the motion of the hammer raised by a water-wheel, or of a point in a string excited by a violin bow. For the first 9 intervals it rises slowly and uniformly, and during the 10th it falls suddenly down.

Fig. 9 represents the motion of the ball which is struck up again as soon as it comes down. Ascent and descent are performed with equal rapidity, whereas in fig. 8 the ascent takes much longer time. But at the lowest point the blow suddenly changes the kind of motion.

Physicists, then, having in their mind such curvilinear forms, representing the law of the motion of sounding bodies, speak briefly of the form of vibration of a sounding body, and assert that the quality of tone depends on the form of vibration. This assertion, which has hitherto been based simply on the fact of our knowing that the quality of the tone could not possibly depend on the periodic time of a vibration, or on its amplitude (p. 10), will be strictly examined hereafter. It will be shewn to be in so far correct that every different quality of tone requires a different form of vibration, but on the other hand it will also appear that different forms of vibration may correspond to the same quality of tone.

On exactly and carefully examining the effect produced on the ear by different forms of vibration, as for example that in fig. 8, corresponding nearly to a violin string, we meet with a strange and unexpected phenomenon, long known indeed to individual musicians and physicists, but commonly regarded as a mere curiosity, its generality and its great significance for all matters relating to musical tones not having been recognised. The ear when its attention has been properly directed to the effect of the vibrations which strike it, does not hear merely that one musical tone whose pitch is determined by the period of the vibrations in the manner already explained, but in addition to this it becomes aware of a whole series of higher musical tones, which we will call the harmonic upper partial tones, and sometimes simply the upper partials of the whole musical tone or note, in contradistinction to the fundamental or prime partial tone or simply the prime, as it may be called, which is the lowest and generally the loudest of all the partial tones and by the pitch of which we judge of the pitch of the whole compound musical tone itself. The series of these upper partial tones is precisely the same for all compound musical tones which correspond to a uniformly periodical motion of the air. It is as follows : —

The first upper partial tone [or second partial tone] is the upper Octave of the prime tone, and makes double the number of vibrations in the same time. If we call the prime \(C\), this upper Octave will be \(c\).

The second upper partial tone [or third partial tone] is the Fifth of this Octave, or \(g\), making three times as many vibrations in the same time as the prime.

The third upper partial tone [or fourth partial tone] is the second higher Octave or \(c'\), making four times as many vibrations as the prime in the same time.

The fourth upper partial tone [or fifth partial tone] is the major Third of this second higher Octave, or \(e'\), with five times as many vibrations as the prime in the same time.

The fifth upper partial tone [or sixth partial tone] is the Fifth of the second higher Octave, or \(g'\), making six times as many vibrations as the prime in the same time.

And thus they go on, becoming continually fainter, to tones making 7, 8, 9, &c., times as many vibrations in the same time, as the prime tone. Or in musical notation

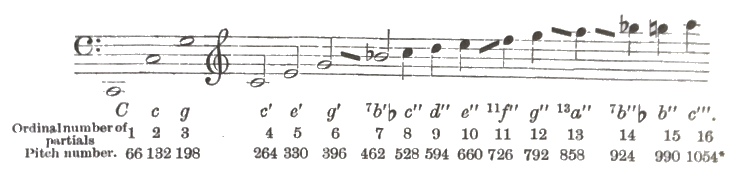
where the figures [in the first line] beneath shew how many times the corresponding pitch number is greater than that of the prime tone [and, taking the lowest note to have 66 vibrations, those in the second line give the pitch numbers of all the other notes].

The whole sensation excited in the ear by a periodic vibration of the air we have called a musical tone. We now find that this is compound, containing a series of different tones, which we distinguish as the constituents or partial tones of the compound. The first of these constituents is the prime partial tone of the compound, and the rest its harmonic upper partial tones. The number which shews the order of any partial tone in the series shews how many times its vibrational number exceeds that of the prime tone.^[16] Thus, the second partial tone makes twice as many, the third three times as many vibrations in the same time as the prime tone, and so on.

G. S. Ohm was the first to declare that there is only one form of vibration which will give rise to no harmonic upper partial tones, and which will therefore consist solely of the prime tone. This is the form of vibration which we have described above as peculiar to the pendulum and tuning-forks, and drawn in figs. 6 and 7 (p. 10). We will call these pendular vibrations, or, since they cannot be analysed into a compound of different tones, simple vibrations. In what sense not merely other musical tones, but all other forms of vibration, may be considered as compound, will be shewn hereafter (Chap. IV.). The terms simple or pendular vibration ^[17], will therefore be used as synonymous. We have hitherto used the expression tone and musical tone indifferently. It is absolutely necessary to distinguish in acoustics first, a musical tone, that is, the impression made by any periodical vibration of the air; secondly a simple tone, that is, the impression produced by a simple or pendular vibration of the air; and thirdly a compound tone, that is, the impression produced by the simultaneous action of several simple tones with certain definite ratios of pitch as already explained. A musical tone may be either simple or compound. For the sake of brevity, tone will be used in the general sense of a musical tone, leaving the context or a prefixed qualification to determine whether it is simple or compound. A compound tone will often be briefly called a note, and a simple tone will also be frequently called a, partial, when used in connection with a compound tone; otherwise, the full expression simple tone will be employed. A note has, properly speaking, no single pitch, as it is made up of various partials each of which has its own pitch. By the pitch of a note or compound tone then we shall therefore mean the pitch of its lowest partial or prime tone. By a chord or combination of tones we mean several musical tones (whether simple or compound) produced by different instruments or different parts of the same instrument so as to be heard at the same time. The facts here adduced shew us then that every musical tone in which harmonic upper partial tones can be distinguished, although produced by a single instrument, may really be considered as in itself a chord or combination of various simple tones.^[18]

Now, since quality of tone, as we have seen, depends on the form of vibration, which also determines the occurrence of upper partial tones, we have to inquire how far differences in quality of tone depend on different force or loudness of upper partials. This inquiry will be found to give a means of clearing up our conceptions of what has hitherto been a perfect enigma, — the nature of quality of tone. And we must then, of course, attempt to explain how the ear manages to analyse every musical tone into a series of partial tones, and what is the meaning of this analysis. These investigations will engage our attention in the following chapters.

[1]Mechanically the force of the oscillations for tones of different pitch is measured by their vis viva, that is, by the square of the greatest velocity attained by the oscillating particles. But the ear has different degrees of sensibility for tones of different pitch, so that no measure can be found for the intensity of the sensation of sound, that is, for the loudness of sound which will hold all pitches. [See the addition to a footnote on p. 75d, referring especially to this passage. — Translator.] ↵

[2][The pitch number was called the 'vibrational number' in the first edition of this translation. The pitch number of a note is commonly called the pitch of the note. By a convenient abbreviation we often write \(a' \; 440\), meaning the note \(a'\) having the pitch number 440; or say that the pitch of \(a'\) is 440 vib. that is, 440 double vibrations in a second. The second term frequency, which I have introduced into the text, as it is much used by acousticians, properly represents the number of times that any periodically recurring event happens in one second of time, and, applied to double vibrations, it means the same as pitch number. The pitch of a musical instrument is the pitch of the note by which it is tuned. But as pitch is properly a sensation, it is necessary here to distinguish from this sensation the pitch number or frequency of vibration by which it is measured. The larger the pitch number, the higher or sharper the pitch is said to be. The lower the pitch number the deeper or flatter the pitch. These are all metaphorical expressions which must be taken strictly in this sense. — Translator.]↵

[3][An account of the more exact modern methods is given in App. XX. sect. B. — Translator.]↵

[4]See Appendix I.↵

[5][Pronounce Dóh-veh, in two syllables. — Translator.]↵

[6][When two notes have different pitch numbers, there is said to be an interval between them. This gives rise to a sensation, very differently appreciated by different individuals, but in all cases the interval is measured by the ratio of the pitch numbers, and, for some purposes, more conveniently by other numbers called cents, derived from these ratios, as explained in App. XX. sect. C. The names of all the intervals usually distinguished are also given in App. XX. sect. D., with the corresponding ratios and cents. These names were in the first place derived from the ordinal number of the note in the scales, or successions of continually sharper notes. The Octave is the eighth note in the major scale. An octave is a set of notes lying within an Octave. Observe that in this translation all names of intervals commence with a capital letter, to prevent ambiguity, as almost all such words are also used in other senses. — Translator.]↵

[7][As the monochord is very liable to error, these results were happy generalisations from necessarily imperfect experiments. — Translator.]↵

[8][English works use strokes above and below the letters, which are typographically inconvenient. Hence the German notation is retained. — Translator.] ↵

[9][The note C in the small octave was once emitted by an organ pipe 4 feet in length : thus Bédos (L’Art du Facteur d’Orgues, 1766) made it 4 old French feet, which gave a note a full Semitone flatter than a pipe of 4 English feet. But in modem organs not even so much as 4 English feet are used. Organ builders, however, in all countries retain the names of the octaves as here given, which must be considered merely to determine the place on the staff, as noted in the text, independently of the precise pitch. — Translator.] ↵

[10]The Paris Academy has lately fixed the pitch number of the same note at 435. This is called 870 by the Academy, because French physicists have adopted the inconvenient habit of counting the forward motion of a swinging body as one vibration, and the backward as another, so that the whole vibration is counted as two. This method of counting has been taken from the seconds pendulum, which ticks once in going forward and once again on returning. For symmetrical backward and forward motions it would be indifferent by which method we counted, but for non-symmetrical musical vibrations which are of constant occurrence, the French method of counting is very inconvenient. The number 440 gives fewer fractions for the first [just] major scale of \(C\), than \(a' = 435\). The difference of pitch is less than a comma. [The practical settlement of pitch has no relation to such arithmetical considerations as are here suggested, but depends on the compass of the human voice and the music written for it at different times. An Abstract of my History of Musical Pitch is given in Appendix XX. sect. H. Scheibler's proposal, named in the text, was chosen, as he tells us (Der Tonmesser , 1834, p. 53), as being the mean between the limits of pitch within which Viennese pianofortes at that time rose and fell by heat and cold, which he reckons at \(\tfrac34\) vibration either way. That this proposal had no reference to the expression of the just major scale in whole numbers, is shewn by she fact that he proposed it for an equally tempered scale, for which he calculated the pitch numbers to four places of decimals, and for which, of course, none but the octaves of \(a'\) are expressible by whole numbers. — Translator.] ↵

[11]

[As it is important that students should be able to hear the exact intervals and pitches spoken of throughout this book, and as it is quite impossible to do so on any ordinary instrument, I have contrived a specially-tuned harmonium, called an Harmonical, fully described in App. XX. sect. F. No. 1, which Messrs. Moore & Moore, 104 Bishopsgate Street, will, in the interests of science, supply to order, for the moderate sum of 165s. The following are the pitch numbers of the first four octaves, the tuning of the fifth octave will be explained in App. XX. sect. F. The names of the notes are in the notation of the latter part of Chap. XIV. below. Read the sign \(D_1\) as '\(D\) one,' \(E^1\flat\) as 'one \(E\) flat,' and \(^7B\flat\) as 'seven \(B\) flat'. In playing observe that \(D_1\) is on the ordinary \(D\flat\) or \(C\sharp\) digital, and that \(^7B\flat\) is on the ordinary \(G\flat\) or \(F\sharp\) digital, and that the only keys in which chords can be played are \(C\) major and \(C\) minor, with the minor chord \(D_1FA_1\) and the natural chord of the Ninth \(CE_1G^7B\flat D\). The mode of measuring intervals by ratios and cents is fully explained hereafter, and the results are added for convenience of reference. The pitches of \(c'' \; 528, \; a' \; 440, \; a'^{1}\flat \; 422.4\) and \(^7b'\flat 462\), were taken from forks very carefully tuned by myself to these numbers of vibrations, by means of my unique series of forks described in App. XX., at the end of sect. B.

Harmonical Keyboard

SCALE OF THE HARMONICAL.

Pitch Numbers					Ratios		Cents
Notes	8 foot	4 foot	2 foot	1 foot	Note to Note	\(C\) to Note	Note to Note	\(C\) to Note
\(C\)	66	132	264	528		1:1		0
					9:10		182
\(D_1\)	73\(\tfrac13\)	146\(\tfrac23\)	293\(\tfrac13\)	586\(\tfrac23\)		9:10		182
					80:81		22
\(D\)	74\(\tfrac14\)	148\(\tfrac12\)	297	594		8:9		204
					15:16		112
\(E^1\flat\)	79\(\tfrac15\)	158\(\tfrac25\)	316\(\tfrac45\)	633\(\tfrac35\)		5:6		316
					24:25		70
\(E_1\)	82\(\tfrac12\)	165	330	660		4:5		386
					15:16		112
\(F\)	88	176	352	704		3:4		498
					8:9		204
\(G\)	99	198	396	792		2:3		702
					15:16		112
\(A^1\flat\)	105\(\tfrac35\)	211\(\tfrac15\)	422\(\tfrac25\)	844\(\tfrac45\)		5:8		814
					24:25		70
\(A_1\)	110	220	440	880		3:5		884
					20:21		85
\(^7B\flat\)	115\(\tfrac12\)	231	462	924		4:7		969
					35:36		49
\(B^1\flat\)	118\(\tfrac45\)	237\(\tfrac35\)	474\(\tfrac15\)	950\(\tfrac25\)		5:9		1018
					24:25		70
\(B_1\)	123\(\tfrac34\)	247\(\tfrac12\)	495	990		8:15		1088
					15:16		112
\(C\)	132	264	528	1056		1:2		1200

- Translator.]

↵

[12][The following account of the actual tones used is adapted from my History of Musical Pitch. \(C_{\prime\prime}\), commencement of the 32-foot octave, the lowest tone of very large organs, two Octaves below the lowest tone of the Violon-cello. \(A_{\prime\prime}\), the lowest tone of the largest pianos. \(C_{\prime}\), commencement of the 16-foot octave, the lowest note assigned to the Double Bass in Beethoven's Pastoral Symphony. \(E_{\prime}\), the lowest tone of the German four-stringed Double Bass, the lowest tone mentioned in the text. \(F_{\prime}\), the lowest tone of the English four-stringed Double Bass. \(G_{\prime}\), the lowest tone of the Italian three-stringed Double Bass. \(A_{\prime}\), the lowest tone of the English three-stringed Double Bass. \(C\), commencement of the 8-foot octave, the lowest tone of the Violoncello, written on the second leger line below the bass staff. \(G\), the tone of the third open string of the Violoncello. \(c\), commencement of the 4-foot octave 'tenor \(C\),' the lowest tone of the Vióla, written on the second space of the bass staff, \(d\), the tone of the second open string of the Violoncello, \(f\), the tone signified by the bass or \(F\)-clef. \(g\), the lowest tone of the Violin, \(a\), the tone of the highest open string of the Violoncello, \(c'\), commencement of the 2-foot octave, 'middle \(C\),' written on the leger line between the bass and treble staves, the tone signified by the tenor or \(C\)-clef . \(d'\), the tone of the third open string of the Violin, \(g'\), the tone signified by the treble or \(G\)-clef . \(a'\), the tone of the second open string of the Violin, the 'tuning note' for orchestras, \(c''\), commencement of the 1-foot octave, the usual 'tuning note' for pianos, \(e''\), the tone of the first or highest open string of the Violin, \(c'''\), commencement of the \(\tfrac12\)-foot octave, \(g'''\), the usual highest tone of the Flute. \(c^{\text{iv}}\), commencement of the \(\tfrac14\)-foot octave. \(e^{\text{iv}}\), the highest tone on the Violin, being the double Octave harmonic of the tone of the highest open string. \(a^{\text{iv}}\), the usual highest tone of large pianos. \(d^{\text{v}}\), the highest tone of the piccolo flute. \(e^{\text{viii}}\), the highest tone reached by Appunn’s forks, see next note. — Translator.]↵

[13][Copies of these forks, described in Prof. Preyer’s essay 'On the Limits of the Perception of Tone,' (über die Grenzen der Tonwahrnehmung, 1876, p. 20), are in the South Kensington Museum, Scientific Collection. I have several times tried them. I did not myself find the tones painful or cutting, probably because there was no beating of inharmonic upper partials. It is best to sound them with two violin bows, one giving the octave of the other. The tones can be easily heard at a distance of more than 100 feet in the gallery of the museum. — Translator.]↵

[14][Assuming the undulatory theory, which attributes the sensation of light to the vibrations of a supposed luminous 'ether,' resembling air but more delicate and mobile, then the phenomena of 'interference' enables us to calculate the lengths of waves of light in empty space, &c., hence the numbers of vibrations in a second, and consequently the ratios of these numbers, which will then clearly resemble the ratios of the pitch numbers that measure musical intervals. Assuming, then, that the yellow of the spectrum answers to the tenor \(c\) in music, and Fraunhofer's 'line A' corresponds to the \(G\) below it, Prof. Helmholtz in his Physiological Optics (Handbuch der physiologischen Optik, 1867, p. 237), gives the following analogies between the notes of the piano and the colours of the spectrum : — $$ \begin{alignedat}{5} &F\sharp , \;\;\; \text{end of the Red.} \\ &G , \;\;\; \text{Red.}\\ &G\sharp , \;\;\; \text{Red.}\\ &A , \;\;\; \text{Red.}\\ &A\sharp , \;\;\; \text{Orange-red.}\\ &B , \;\;\; \text{Orange.}\\ &c , \;\;\; \text{Yellow.}\\ &c\sharp , \;\;\; \text{Green.}\\ &d , \;\;\; \text{Greenish-blue.}\\ &d\sharp , \;\;\; \text{Cyanogen-blue.}\\ &e , \;\;\; \text{Indigo-blue.}\\ &f , \;\;\; \text{Violet.}\\ &f\sharp , \;\;\; \text{Violet.}\\ &g , \;\;\; \text{Ultra-violet.}\\ &g\sharp , \;\;\; \text{Ultra-violet.}\\ &a , \;\;\; \text{Ultra-violet.}\\ &a\sharp , \;\;\; \text{Ultra-violet.}\\ &b , \;\;\; \text{Ultra-violet.}\\ \end{alignedat} $$ The scale therefore extends to about a Fourth beyond the octave. — Translator.] ↵

[15][This diagram has been slightly altered to introduce all the first 16 harmonic partials of \(C\) 66 (which, excepting 11 and 13, are given on the Harmonical as harmonic notes), and to shew the notation, symbolising, both in letters and on the staff, the 7th, 11th, and 13th harmonic partials, which are not used in general music. It is easy to shew on the Harmonical that its lowest note, \(C\) of this series, contains all these partials, after the theory of the beats of a disturbed unison has been explained in Chap. VIII. Keep down the note \(C\), and touch in succession the notes, \(c, \; g, \; c', \; e', \; g', \) &c., but in touching the latter press the finger-key such a little way down that the tone of the note is only just audible. This slightly flattens each note, and slow beats can be produced in every case (except, of course, 11 and 13, which are not on the instrument) up to 16. It should also be observed that the pitch of the boat is very nearly that of the upper (not the lower) note in each case. The whole of these 16 harmonics of \(C\) 66 (except the 11th and 13th) can be played at once on the Harmonical by means of the harmonical bar, first without and then with the 7th and 14th. The whole series will be found to sound like a single fine note, and the 7th and 14th to materially increase its richness. The relations of the partials in this case may be studied from the tables in the footnotes to Chap. X.— Translator.] ↵

[16][The ordinal number of a partial tone in general, must be distinguished from the ordinal number of an upper partial tone in particular. For the same tone the former number is always greater by unity than the latter, because the partials in general include the prime, which is reckoned as the first, and the upper partials exclude the prime, which being the lowest partial is of course not an upper partial at all. Thus the partials generally numbered \(2\; 3\; 4\; 5\; 6\; 7\; 8\; 9\) are the same as the upper partials numbered \(1 \;2\; 3\; 4\; 5\; 6\; 7\; 8\) respectively. As even the Author has occasionally failed to carry out this distinction in the original German text, and other writers have constantly neglected it, too much weight cannot be here laid upon it. The presence or absence of the word upper before the word partial must always be carefully observed. It is safer never to speak of an upper partial by its ordinal number, but to call the fifth upper partial the sixth partial, omitting the word upper and increasing the ordinal number by one place. And so in other cases. — Translator.]↵

[17]The law of these vibrations may be popularly explained by means of the construction in fig. 10. Suppose a point to describe the circle of which c is the centre with a uniform velocity, and that an observer stands at a considerable distance in the prolongation of the line e h, so that he does not see the surface of the circle but only its edge, in which case the point will appear merely to move up and down along its diameter a b. This up and down motion would take place exactly according to the law of pendular vibration.

To represent this motion graphically by means of a curve, divide the length e g, supposed to correspond to the time of a single period, into as many (here 12) equal parts as the circumference of the circle, and draw the perpendiculars 1, 2, 3, &c., on the dividing points of the line e g, in order, equal in length to and in the same direction with, those drawn in the circle from the corresponding points 1, 2, 3, &c. In this way we obtain the curve drawn in fig. 10, which agrees in form with that drawn by the tuning-fork, fig. 6, p. 20, but is of a larger size. Mathematically expressed, the distance of the vibrating point from its mean position at any time is equal to the sine of an arc proportional to the corresponding time, and hence the form of simple vibrations are also called the sine-vibrations [and the above curve is also known as the curve of sines]↵

[18] [The above paragraph relating to the English terms used in this translation, necessarily differs in many respects from the original, in which a justification is given of the use made by the Author of certain German expressions. It has been my object to employ terms which should be thoroughly English, and should not in any way recall the German words. The word tone in English is extremely ambiguous. Prof. Tyndall (Lectures on Sound, 2nd ed. 1869, p. 117) has ventured to define a tone as a simple tone, in agreement with Prof. Helmholtz, who in the present passage limits the German word Ton in the same way. But I felt that an English reader could not be safely trusted to keep this very peculiar and important class of musical tones, which he has very rarely or never heard separately, invariably distinct from those musical tones with which he is familiar, unless the word tone were uniformly qualified by the epithet simple. The only exception I could make was in the case of a partial tone, which is received at once as a new conception. Even Prof. Helmholtz himself has not succeeded in using his word Ton consistently for a simple tone only, and this was an additional warning to me. English musicians have been also in the habit of using tone to signify a certain musical interval, and semitone for half of that interval, on the equally tempered scale. In this case I write Tone and Semitone with capital initials, a practice which, as already explained (note, p. 13), I have found convenient for the names of all intervals, as Thirds, Fifths, &c. Prof. Helmholtz uses the word Klang for a musical tone, which generally, but not always, means a compound tone. Prof. Tyndall (ibid.) therefore proposes to use the English word clang in the same sense. But clang has already a meaning in English, thus defined by Webster: 'a sharp shrill sound, made by striking together metallic substances, or sonorous bodies, as the clang of arms, or any like sound, as the clang of trumpets. This word implies a degree of harshness in the sound, or more harshness than clink.' Interpreted scientifically, then, clang according to this definition, is either noise or one of those musical tones with inharmonic upper partials which will be subsequently explained. It is therefore totally adapted to represent a musical tone in general, for which the simple word tone seems eminently suited, being of course originally the tone produced by a stretched string. The common word note, properly the mark by which a musical tone is written, will also, in accordance with the general practice of musicians, be used for a musical tone, which is generally compound, without necessarily implying that it is one of the few recognised tones in our musical scale. Of course, if clang could not be used, Prof. Tyndall's suggestion to translate Prof. Helmholtz's Klangfarbe by clangtint (ibid.) fell to the ground. I can find no valid reason for supplanting the time-honoured expression quality of tone. Prof. Tyndall (ibid.) quotes Dr. Young to the effect that 'this quality of sound is sometimes called its register, colour, or timbre'. Register has a distinct meaning in vocal music which must not be disturbed. Timbre, properly a kettledrum, then a helmet, then the coat of arms surmounted with a helmet, then the official stamp bearing that coat of arms (now used in France for a postage label), and then the mark which declared a thing to be what it pretends to be, Burns's 'guinea’s stamp,' is a foreign word, often odiously mispronounced, and not worth preserving. Colour I have never met with as applied to music, except at most as a passing metaphorical expression. But the difference of tones in quality is familiar to our language. Then as to the Partial Tones, Prof. Helmholtz uses Theiltöne and Partial-töne, which are aptly Englished by partial simple tones. The words simple and tone, however, may be omitted when partials is employed, as partials are necessarily both tones and simple. The constituent tones of a chord may be either simple or compound. The Grundton or fundamental tone of a compound tone then becomes its prime tone, or briefly its prime. The Grundton or root of a chord will be further explained hereafter. Upper partial (simple) tones, that is, the partials exclusive of the prime, even when harmonic (that is, for the most part, belonging to the first six partial tones), must be distinguished from the sounds usually called harmonics when produced on a violin or harp for instance, for such harmonics are not necessarily simple tones, but are more generally compounds of some of the complete series of partial tones belonging to the musical tone of the whole string, selected by damping the remainder. The fading harmonics heard in listening to the sound of a pianoforte string, struck and undamped, as the sound dies away, are also compound and not simple partial tones, but as they have the successive partials for their successive primes, they have the pitch of those partials. But these fading harmonics are not regular compound tones of the kind described on p. 22, because the lower partials are absent one after another. Both sets of harmonics serve to indicate the existence and place of the partials. But they are no more those upper partial tones themselves, than the original compound tone of the string is its own prime. Great confusion of thought having, to my own knowledge, arisen from confounding such harmonics with upper partial tones, I have generally avoided using the ambiguous substantive harmonic. Properly speaking the harmonics of any compound tone are other compound tones of which the primes are partials of the original compound tone of which they are said to be harmonics. Prof. Helmholtz's term Obertöne is merely a contraction for Oberpartialtöne, but the casual resemblance of the sounds of ober and over, has led Prof. Tyndall to the erroneous translation overtones. The German ober is an adjective meaning upper, but the English preposition over is equivalent to the German preposition über. Compare Oberzahn, an 'upper tooth,' i.e., a tooth in the upper jaw, with Ueberzahn, an 'overtooth,' i.e., one grown over another, a projecting tooth. The continual recurrence of such words as clang, clangtint, overtone, would combine to give a strange un-English appearance to a translation from the German. On the contrary I have endeavoured to put it into as straightforward English as possible. But for those acquainted with the original and with Prof. Tyndall’s work, this explanation seemed necessary. Finally I would caution the reader against using overtones for partial tones in general, as almost every one who adopts Prof. Tyndall's word is in the habit of doing. Indeed I have in the course of this translation observed, that even Prof. Helmholtz himself has been occasionally misled to employ Obertöne in the same loose manner. See my remarks in note, p. 23. — Translator.]↵