
Towards the close of Chapter I. (p. 21d), we found that differences in the quality of musical tones must depend on the form of the vibration of the air. The reasons for this assertion were only negative. We have seen that force depended on amplitude, and pitch on rapidity of vibration: nothing else was left to distinguish quality but vibrational form. We then proceeded to shew that the existence and force of the upper partial tones which accompanied the prime depend also on the vibrational form, and hence we could not but conclude that musical tones of the same quality would always exhibit the same combination of partials, seeing that the peculiar vibrational form which excites in the ear the sensation of a certain quality of tone, must always evoke the sensation of its corresponding upper partials. The question then arises, can, and if so, to what extent can the differences of musical quality be reduced to the combination of different partial tones with different intensities in different musical tones? At the conclusion of last chapter (p. 60d), we saw that even artificially combined simple tones were capable of fusing into a musical tone of a quality distinctly different from that of either of its constituents, and that consequently the existence of a new upper partial really altered the quality of a tone. By this means we gained a clue to the hitherto enigmatical nature of quality of tone, and to the cause of its varieties.
There has been a general inclination to credit quality with all possible peculiarities of musical tones that were not evidently due to force and pitch. This was correct to the extent that quality of tone was merely a negative conception. But very slight consideration will suffice to shew that many of these peculiarities of musical tones depend upon the way in which they begin and end. The methods of attacking and releasing tones are sometimes so characteristic that for the human voice they have been noted by a series of different letters. To these belong the explosive consonants B, D, G, and P, T, K. The effects of these letters are produced by opening the closed, or closing the open passage through the mouth. For B and P the closure is made by the lips, for D and T by the tongue and upper teeth,[1] for G and K by the back of the tongue and soft palate. The series of the mediae B, D, G is distinguished from that of the tenues P, T, K, by the glottis being sufficiently narrowed, when the closure of the former is released, to produce voice, or at least the rustle of whisper, whereas for the latter or tenues the glottis is wide open, [2] and cannot sound. The mediae are therefore accompanied by voice, which is capable of commencing at the beginning of a syllable an instant before the opening of the mouth, and of lasting at the end of a syllable a moment after the closure of the mouth, because some air can be still driven into the closed cavity of the mouth and the vibration of the vocal chords in the larynx can be still maintained. On account of the narrowing of the glottis the influx of air is more moderate, and the noise of the wind less sharp for the mediae than the tenues, which, being spoken with open glottis, allow of a great deal of wind being forced at once from the chest.[3] At the same time the resonance of the cavity of the mouth, which, as we shall more clearly understand further on, exercises a great influence on the vowels, varies its pitch, corresponding to the rapid alterations in the magnitude of its volume and orifice, and this brings about a corresponding rapid variation in the quality of the speech sound.
As with consonants, the differences in the quality of tone of struck strings, also partly depends on the rapidity with which the tone dies away. When the strings have little mass (such as those of gut), and are fastened to a very mobile sounding board (as for a violin, guitar, or zither), or when the parts on which they rest or which they touch are but slightly elastic (as when the violin strings, for example, are pressed on the finger board by the soft point of the finger), their vibrations rapidly disappear after striking, and the tone is dry, short, and without ring, as in the pizzicato of a violin. But if the strings are of metal wire, and hence of greater weight and tension, and if they are attached to strong heavy bridges which cannot be much shaken, they give out their vibrations slowly to the air and the sounding board; their vibrations continue longer, their tone is more durable and fuller, as in the pianoforte, but is comparatively less powerful and penetrating than that of gut strings, which give up their tone more readily when struck with the same force. Hence the pizzicato of bowed instruments when well executed is much more piercing than the tone of a pianoforte. Pianofortes with their strong and heavy supports for the strings have, consequently, for the same thickness of string, a less penetrating but a much more lasting tone than those instruments of which the supports for the strings are lighter.
It is very characteristic of brass instruments, as trumpets and trombones, that their tones commence abruptly and sluggishly. The various tones in these instruments are produced by exciting different upper partials through different styles of blowing, which serve to throw the column of air into vibrating portions of different numbers and lengths similar to those on a string. It always requires a certain amount of effort to excite the new condition of vibration in place of the old, but when once established it is maintained with less exertion. On the other hand, the transition from one tone to another is easy for wooden wind instruments, as the flute, oboe, and clarinet, where the length of the column of air is readily changed by application of the fingers to the side holes and keys, and where the style of blowing has not to be materially altered.
These examples will suffice to shew how certain characteristic peculiarities in the tones of several instruments depend on the mode in which they begin and end. When we speak in what follows of musical quality of tone, we shall disregard these peculiarities of beginning and ending, and confine our attention to the peculiarities of the musical tone which continues uniformly.
But even when a musical tone continues with uniform or variable intensity, it is mixed up, in the general methods of excitement, with certain noises, which express greater or less irregularities in the motion of the air. In wind instruments where the tones are maintained by a stream of air, we generally hear more or less whizzing and hissing of the air which breaks against the sharp edges of the mouthpiece. In strings, rods, or plates excited by a violin bow, we usually hear a good deal of noise from the rubbing. The hairs of the bow are naturally full of many minute irregularities, the resinous coating is not spread over it with absolute evenness, and there are also little inequalities in the motion of the arm which holds the bow and in the amount of pressure, all of which influence the motion of the string, and make the tone of a bad instrument or an unskilful performer rough, scraping, and variable. We shall not be able to explain the nature of the motions of the air and sensations of the ear which correspond to these noises till we have investigated the conception of beats. Those who listen to music make themselves deaf to these noises by purposely withdrawing attention from them, but a slight amount of attention generally makes them very evident for all tones produced by blowing or rubbing. It is well known that most consonants in human speech are characterised by the maintenance of similar noises, as F, V ; S, Z ; TH in thin and in then; the Scotch and German guttural CH, and Dutch G. For some the tone is made still more irregular by trilling parts of the mouth, as for R and L. In the case of R the stream of air is periodically entirely interrupted by trilling the uvula[4] or the tip of the tongue; and we thus 'obtain an intermitting sound to which these interruptions give a peculiar jarring character. In the case of L the soft side edges of the tongue are moved by the stream of air, and, without completely interrupting the tone, produce inequalities in its strength.
Even the vowels themselves are not free from such noises, although they are kept more in the background by the musical character of the tones of the voice. Bonders first drew attention to these noises, which are partly identical with those which are produced when the corresponding vowels are indicated in low voiceless speech. They are strongest for ee in see, the French u in vu (which is nearly the same as the Norfolk and Devon oo in too), and for oo in too. For these vowels they can be made audible even when speaking aloud.[5] By simply increasing their force the vowel ee in see becomes the consonant y in you, and the vowel oo in too the consonant w in wan.[6] For a in art, a in at, e in met, there, and o in more, the noises appear to me to be produced in the glottis alone when speaking gently, and to be absorbed into the voice when speaking aloud.[7] It is remarkable that in speaking, the vowels a in art, a in at, and e in met, there, are produced with less musical tone than in singing. It seems as if a feeling of greater compression in the larynx caused the tuneful tone of the voice to give way to one of a more jarring character which admits of more evident articulation. The greater intensity thus given to the noises, appears in this case to facilitate the characterisation of the peculiar vowel quality. In singing, on the contrary, we try to favour the musical part of its quality and hence often render the articulation somewhat obscure.[8]
Such accompanying noises and little inequalities in the motion of the air, furnish much that is characteristic in the tones of musical instruments, and in the vocal tones of speech which correspond to the different positions of the mouth; but besides these there are numerous peculiarities of quality belonging to the musical tone proper, that is, to the perfectly regular portion of the motion of the air. The importance of these can be better appreciated by listening to musical instruments or human voices, from such a distance that the comparatively weaker noises are no longer audible. Notwithstanding the absence of these noises, it is generally possible to discriminate the different musical instruments, although it must be acknowledged that under such circumstances the tone of a French horn may be occasionally mistaken for that of the singing voice, or a violoncello may be confused with an harmonium. For the human voice, consonants first disappear at a distance, because they are characterised by noises, but M, N, and the vowels If can be distinguished at a greater distance. The formation of M and N in so far resembles that of vowels, that no noise of wind is generated in any part of the cavity of the mouth, which is perfectly closed, and the sound of the voice escapes through the nose. The mouth merely forms a resonance chamber which alters the quality of tone. It is interesting in calm weather to listen to the voices of men who are descending from high hills to the plain. Words can no longer be recognised, or at most only such as are composed of M, N, and vowels, as Mamma, No, Noon. But the vowels contained in the spoken words are easily distinguished. Wanting the thread which connects them into words and sentences, they, form a strange series of alternations of quality and singular inflections of tone.
In the present chapter we shall at first disregard all irregular portions of the motion of the air, and the mode in which sounds commence or terminate, directing our attention solely to the musical part of the tone, properly so called, which corresponds to a uniformly sustained and regularly periodic motion of the air, and we shall endeavour to discover the relations between the quality of the sound and its composition out of individual simple tones. The peculiarities of quality of sound belonging to this division, we shall briefly call its musical quality.
The object of the present chapter is, therefore, to describe the different composition of musical tones as produced by different instruments, for the purpose of shewing how different modes of combining the upper partial tones correspond to characteristic varieties of musical quality. Certain general rules will result for the arrangement of the upper partials which answer to such species of musical quality as are called, soft, piercing, braying, hollow or poor, full or rich, dull, bright, crisp, pungent, and so on. Independently of our immediate object (the determination of the physiological action of the ear in the discrimination of musical quality, which is reserved for the following chapter), the results of this investigation are important for the resolution of purely musical questions in later chapters, because they shew us how rich in upper partials, good musical qualities of tone are found to be, and also point out the peculiarities of musical quality favoured on those musical instruments, for which the quality of tone has been to some extent abandoned to the caprice of the maker.
Since physicists have worked comparatively little at this subject I shall be forced to enter somewhat more minutely into the mechanism by which the tones of several instruments are produced, than will be, perhaps, agreeable to many of my readers. For such the principal results collected at the end of this chapter will suffice. On the other hand, I must ask indulgence for leaving many large gaps in this almost unexplored region, and for confining myself principally to instruments sufficiently well known for us to obtain a tolerably satisfactory view of the source of their tones. In this inquiry lie rich materials for interesting acoustical work. But I have felt bound to confine myself to what was necessary for the continuation of the present investigation.
We begin with such musical tones as are not decomposable, but consist of a single simple tone. These are most readily and purely produced by holding a struck tuning-fork over the mouth of a resonance tube, as has been described in the last chapter (p. 54d).[9] These tones are uncommonly soft and free from all shrillness and roughness. As already remarked, they appear to lie comparatively deep, so that such as correspond to the deep tones of a bass voice produce the impression of a most remarkable and unusual depth. The musical quality of such deep simple tones is also rather dull. The simple tones of the soprano pitch sound bright, but even those corresponding to the highest tones of a soprano voice are very soft, without a trace of that cutting, rasping shrillness which is displayed by most instruments at such pitches, with the exception, perhaps, of the flute, for which the tones are very nearly simple, being accompanied with very few and faint upper partials. Among vowels, the oo in too comes nearest to a simple tone, but even this vowel is not entirely free from upper partials. On comparing the musical quality of a simple tone thus produced with that of a compound tone in which the first harmonic upper partial tones are developed, the latter will be found to be more tuneful, metallic, and brilliant. Even the vowel oo in too, although the dullest and least tuneful of all vowels, is sensibly more brilliant and less dull than a simple tone of the same pitch. The series of the first six partials of a compound tone may be regarded musically as a major chord with a very predominant fundamental tone, and in fact the musical quality of a compound tone possessing these partials, as, for example, a fine singing voice, when heard beside a simple tone, very distinctly produces the agreeable effect of a consonant chord.
Since the form of simple waves of known periodic time is completely given when their amplitude is given, simple tones of the same pitch can only differ in force and not in musical quality. In fact, the difference of quality remains perfectly indistinguishable, whether the simple tone is conducted to the external air in the preceding methods by a tuning-fork and a resonance tube of any given material, glass, metal, or pasteboard, or by a string, provided only that we guard against any chattering in the apparatus.
Simple tones accompanied only by the noise of rushing wind can also be produced, as already mentioned, by blowing over the mouth of bottles with necks (p. 60c). If we disregard the friction of the air, the proper musical quality of such tones is really the same as that produced by tuning-forks.
Nearest to musical tones without any upper partials are those with secondary tones which are inharmonic to the prime, and such tones, therefore, in strictness, should not be reckoned as musical tones at all. They are exceptionally used in artistic music, but only when it is contrived that the prime tone should be so much more powerful than the secondary tones, that the existence of the latter may be ignored. Hence they are placed here next to the simple tones, because musically they are available only for the more or less good simple tones which they represent. The first of these are tuning-forks themselves, when they are struck and applied to a sounding board, or brought very near the ear. The [inharmonic] upper partials of tuning-forks lie very high. In those which I have examined, the first made from 5.8 to 6.6 as many vibrations in the same time as the prime tone, and hence lay between its third diminished Fifth and major Sixth. The pitch numbers of these high upper partial tones were to one another as the squares of the odd numbers. In the time that the first upper partial would execute 3x3 = 9 vibrations, the next would execute 5x5 = 25, and the next 7x7 = 49, and so on. Their pitch, therefore, increases with extraordinary rapidity, and they are usually all inharmonic with the prime, though some of them may exceptionally become harmonic. If we call the prime tone of the fork c, the next succeeding tones are nearly \(a''\flat,\; d' \; \grave{}\; ',\; c\grave{}\;'\sharp\).[10] These high secondary tones produce a bright inharmonic clink, which is easily heard at a considerable distance when the fork is first struck, whereas when it is brought close to the ear, the prime tone alone is heard. The ear readily separates the prime from the upper tones and has no inclination to fuse them. The high simple tones usually die off rapidly, while the prime tone remains audible for a long time. It should be remarked, however, that the mutual relations of the proper tones of tuning-forks differ somewhat according to the form of the fork, and hence the above indications must be looked upon as merely approximate. In theoretical determinations of the upper partial tones, each prong of the fork may be regarded as a rod fixed at one end.
The same relations hold for straight elastic rods, which, as already mentioned, when struck, give rather high inharmonic upper partial tones. When such a rod is firmly supported at the two nodal lines of its prime tone, the continuance of that tone is favoured in preference to the other higher tones, and hence the latter disturb the effect very slightly, more especially as they rapidly die away after the rod has been struck. Such rods, however, are not suitable for real artistic music, although they have lately been introduced for military and dance music on account of their penetrating qualities of tone. Glass rods or plates, and wooden rods, were formerly used in this way for the glass harmonicon and the straw-fiddle or wood harmonicon. The rods were inserted between two pairs of intertwisted strings, which grasped them at their two nodal lines. The wooden rods in the German straw-fiddle were simply laid on straw cylinders. They were struck with hammers of wood or cork.
The only effect of the material of the rods on the quality of tone in these cases, consists in the greater or less length of time that it allows the proper tones at different pitches to continue. These secondary tones, including the higher ones, usually continue to sound longest in elastic metal of fine uniform consistency, because its greater mass gives it a greater tendency to continue in any state of motion which it has once assumed, and among metals the most perfect elasticity is found in steel, and the better alloys of copper and zinc, or copper and tin. In slightly alloyed precious metals, their greater specific gravity lengthens the duration of the tone, notwithstanding their inferior elasticity. Superior elasticity appears to favour the continuance of the higher proper tones, because imperfect elasticity and friction generally seems to damp rapid more quickly than slow vibrations. Hence I think that I may describe the general characteristic of what is usually called a metallic quality of tone, as the comparatively continuous and uniform maintenance of higher upper partial tones. The quality of tone for glass is similar; but as it breaks when violently agitated, the tone is always weak and

soft, and it is also comparatively high, and dies rapidly away, on account of the smaller mass of the vibrating body. In wood the mass is small, the internal structure comparatively rough, being full of countless interstices, and the elasticity also comparatively imperfect, so that the proper tones, especially the higher ones, rapidly die away. And for this reason the straw-fiddle or wood harmonicon is perhaps more satisfactory to a musical ear, than harmonicons formed of steel or glass rods or plates, with their piercing inharmonic upper partial tones, — at least so far as simple tones are suitable for music at all, of which I shall have to speak later on.[11]
Click the mouse on a part of the membrane to watch the effect of hitting it with a drumstick (from below)
For all of these instruments which have to be struck, the hammers are made of wood or cork, and covered with leather. This renders the highest upper partials much weaker than if only hard metal hammers were employed. Greater hardness of the striking mass produces greater discontinuities in the original motion of the plate. The influence exerted by the manner of striking will be considered more in detail, in reference to strings, where it is also of much importance.
According to Chladni’s discoveries, elastic plates, cut in circular, oval, square, oblong, triangular, or hexagonal forms, will sound in a great number of different vibrational forms, usually producing simple tones which are mutually inharmonic. Fig. 21 gives the more simple vibrational forms of a circular plate. Much more complicated forms occur when several circles or additional diameters appear as nodal lines, or where both circles and diameters occur. Supposing the vibrational form A to give the tone \(c\), the others give the following proper tones: —
| Number of Nodal Circles | Number of Diameters | |||||
| 0 | 1 | 2 | 3 | 4 | 5 | |
| 0 | ||||||
| 1 | ||||||
| 2 | ||||||
This shews that many proper tones of nearly the same pitch are produced by a plate of this kind. When a plate is struck, those proper tones which have no node at the point struck, will all sound together. To obtain a particular determinate tone it is of advantage to support the plate in points which lie in the nodal lines of that tone; because those proper tones which have no node in those points will then die off more rapidly. For example, if a circular plate is supported at If 3 points in the nodal circle of fig. 21, C (p. 71c), and is struck exactly in its middle, the simple tone called \(g\sharp\) in the table, which belongs to that form, will be heard, and all those other proper tones which have diameters as some of their nodal lines[12] will be very weak, for example, \(c, \; d', \; c'', \; g'', \; b'\flat\) in the table. In the same way the tone \(g''\sharp\) with two nodal circles, dies off immediately, because the points of support fall on one of its ventral segments, and the first proper tone which can sound loudly at the same time is that corresponding to three nodal circles, one of its nodal lines being near to that of No. 2. But this is 3 Octaves and more than a whole Tone higher than the proper tone of No. 2, and on account of this great interval does not disturb the latter. Hence a disc thus struck gives a tolerably good musical tone, whereas plates in general produce sounds composed of many in harmonic proper tones of nearly the same pitch, giving an empty tin-kettle sort of quality, which cannot be used in music. But even when the disc is properly supported the tone dies away rapidly, at least in the case of glass plates, because contact at many points, even when nodal, sensibly impedes the freedom of vibration.
The sound of bells is also accompanied by inharmonic secondary tones, which, however, do not lie so close to one another as those of flat plates. The vibrations which usually arise have 4, 6, 8, 10, &c., nodal lines extending from the vertex of the bell to its margin, at equal intervals from each other. The corresponding proper tones for glass bells which have approximatively the same thickness throughout, are nearly as the squares of the numbers 2, 3, 4, 5, so that if we call the lowest tone c, we have for the
| Number of nodal lines | 4 | 6 | 8 | 10 | 12 |
| Tones | \(c\) | \(d'+\) | \(c''\) | \(g''\sharp\) | \(d'''+\) |
| Cents |
|
|
|
|
|
The tones, however, vary with the greater or less thickness of the wall of the K bell towards the margin, and it appears to be an essential point in the art of casting bells, to make the deeper proper tones mutually harmonic by giving the bell a certain empirical form. According to the observations of the organist Gleitz,[13] the bell cast for the cathedral at Erfurt in 1477 has the following proper tones: \(E, e, g\sharp, b, e', g'\sharp, b', c''\sharp\) The [former] bell of St. Paul’s, London, gave \(a\) and \(c'\sharp\). Hemony of Zütphen, a master in the seventeenth century, required a good bell to have three Octaves, two Fifths, one major and one minor Third. The deepest tone is not the strongest. The body of the bell when struck gives a deeper tone than the 'sound bow,' but the latter gives the loudest tone. Probably other vibrational forms of bells are also possible in which nodal circles are formed parallel to the margin. But these seemed to be produced with difficulty and have not yet been examined.
If a bell is not perfectly symmetrical in respect to its axis, if, for example, the wall is a little thicker at one point of its circumference than at another, it will give, on being struck, two different tones of very nearly the same pitch, which will 'beat' together. Four points on the margin will be found, separated from each other by quarter-circles, in which only one of these tones can be heard without accompanying beats, and four others, half-way between the pairs of the others, where the second tone only sounds. If the bell is struck elsewhere both tones are heard, producing beats, and such beats may be perceived in most bells as their tone dies gradually away.
Stretched membranes have also inharmonic proper tones of nearly the same pitch. For a circular membrane, of which the deepest tone is c, these are, in a vacuum and arranged in order of pitch, as follows :
|
|
Tone | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
These tones rapidly die out. If the membranes sound in air,[15] or are associated with an air chamber, as in the kettledrum, the relation of the proper tones may be altered. No detailed investigations have yet been made on the secondary tones of the kettledrum. The kettledrum is used in artistic music, but only to mark certain accents. It is tuned, indeed, but only to prevent injury to the harmony, not for the purpose of filling up chords.
The common character of the instruments hitherto described is, that, when struck they produce inharmonic upper partial tones. If these are of nearly the same pitch as the prime tone, their quality of sound is in the highest degree unmusical, bad, and tinkettly. If the secondary tones are of very different pitch from the prime, and weak in force, the quality of sound is more musical, as for example in tuning-forks, harmonicons of rods, and bells; and such tones are applicable for marches and other boisterous music, principally intended to mark time. But for really artistic music, such instruments as these have always been rejected, as they ought to be, for the inharmonic secondary tones, although they rapidly die away, always disturb the harmony most unpleasantly, renewed as they are at every fresh blow. A very striking example of this was furnished by a company of bellringers, said to be Scotch, that lately travelled about Germany, and performed all kinds of musical pieces, some of which had an artistic character. The accuracy and skill of the performance was undeniable, but the musical effect was detestable, on account of the heap of false secondary tones which accompanied the music, although care was taken to damp each bell as soon as the proper duration of its note had expired, by placing it on a table covered with cloth.
Sonorous bodies with inharmonic partials, may be also set in action by violin bows, and then by properly damping them in a nodal line of the desired tone, the secondary tones which lie near it can be prevented from interfering. One simple tone then predominates distinctly, and it might consequently be used for musical purposes. But when the violin bow is applied to any bodies with inharmonic upper partial tones, as tuning-forks, plates, bells, we hear a strong scratching sound, which on investigation with resonators, is found to consist mainly of these same inharmonic secondary tones of such bodies, not sounding continuously but only in short irregular fits and starts. Intermittent tones, as I have already noted, produce the effect of grating or scratching. It is only when the body excited by the violin bow has harmonic upper partials, that it can perfectly accommodate itself to every impulse of the bow, and give a really musical quality of tone. The reason of this is that any required periodic motion such as the bow aims at producing, can be compounded of motions corresponding to harmonic upper partial tones, but not of other, inharmonic vibrations.
We now proceed to the analysis of musical tones proper, which are characterised by harmonic upper partials. These may be best classified according to their mode of excitement: 1. By striking. 2. By bowing. 3. By blowing against a sharp edge. 4. By blowing against elastic tongues or vibrators. The two first classes comprehend stringed instruments alone, as longitudinally vibrating rods, the only other instruments producing harmonic upper partial tones, are not used for musical purposes. The third class embraces flutes and the flute or flue pipes of organs; the fourth all other wind instruments, including the human voice.
Strings excited by Striking. — Among musical instruments at present in use, this section embraces the pianoforte, harp, guitar, and zither; among physical, the monochord, arranged for an accurate examination of the laws controlling the vibrations of strings; the pizzicato of bowed instruments must also be placed in this category. We have already mentioned that the musical tones produced by strings which are struck or plucked, contain numerous upper partial tones. We have the advantage of possessing a complete theory for the motion of plucked strings, by which the force of their upper partial tones may be determined. In the last chapter we compared some of the conclusions of this theory with the results of experiment, and found them agree. A similarly complete theory may be formed for the case of a string which has been struck in one of its points by a hard sharp edge. The problem is not so simple when soft elastic hammers are used, such as those of the pianoforte, but even in this case it is possible to assign a theory for the motion of the string which embraces at least the most essential features of the process, and indicates the force of the upper partial tones.[16]
Click on a box to see how different styles of playing affect the harmonics of a guitar string.
Below is the harmonic analysis of each note played accordingly:
The force of the upper partial tones in a struck string, depends in general on: —
1. The nature of the stroke.
2. The place struck.
3. The density, rigidity, and elasticity of the string.
First, as to the nature of the stroke. The string may be plucked, by drawing it on one side with the finger or a point (the plectrum, or the ring of the zitherplayer), and then letting it go. This is a usual mode of exciting a string in a great number of ancient and modern stringed instruments. Among the modern, I need only mention the harp, guitar, and zither. Or else the string may be struck with a hammer-shaped body, as in the pianoforte.[17] I have already remarked that the strength and number of the upper partial tones increases with the number and abruptness of the discontinuities in the motion excited. This fact determines the various modes of exciting a string. When a string is plucked, the finger, before quitting it, removes it from its position of rest throughout its whole length. A discontinuity in the string arises only by its forming a more or less acute angle at the place where it wraps itself about the finger or point. The angle is more acute for a sharp point than for the finger. Hence the sharp point produces a shriller tone with a greater number of high tinkling upper partials, than the finger. But in each case the intensity of the prime tone exceeds that of any upper partial. If the string is struck with a sharp-edged metallic hammer which rebounds instantly, only the one single point struck is directly set in motion. Immediately after the blow the remainder of the string is at rest. It does not move until a wave of deflection rises, and runs backwards and forwards over the string. This limitation of the original motion to a single point produces the most abrupt discontinuities, and a corresponding long series of upper partial tones, having intensities,[18] in most cases equalling or even surpassing that of the prime. When the hammer is soft and elastic, the motion has time to spread before the hammer rebounds. When thus struck the point of the string in contact with such a hammer is not set in motion with a jerk, but increases gradually and continuously in velocity during the contact. The discontinuity of the motion is consequently much less, diminishing as the softness of the hammer increases, and the force of the higher upper partial tones is correspondingly decreased.
We can easily convince ourselves of the correctness of these statements by opening the lid of any pianoforte, and, keeping one of the digitals down with a weight, so as to free the string from the damper, plucking the string at pleasure with a finger or a point, and striking it with a metallic edge or the pianoforte hammer itself. The qualities of tone thus obtained will be entirely different. When the string is struck or plucked with hard metal, the tone is piercing and tingling, and a little attention enables us to hear a multitude of very high partial tones. These disappear, and the tone of the string becomes less bright, but softer, and more harmonious, when we pluck the string with the soft finger or strike it with the soft hammer of the instrument. We also readily recognise the different loudness of the prime tone. When we strike with metal, the prime tone is scarcely heard and the quality of tone is correspondingly poor. The peculiar quality of tone commonly termed poverty, as opposed to richness, arises from the upper partials being comparatively too strong for the prime tone. The prime tone is heard best when the string is plucked with a soft finger, which produces a rich and yet harmonious quality of tone. The prime tone is not so strong, at least in the middle and deeper octaves of the instrument, when the strings are struck with the pianoforte hammer, as when they are plucked with the finger.
This app simulates a struck string, similar to that in a piano. Use the slider to increase how hard the hammer is, with the hardest option on the right. The box below displays how long the string is struck for. Click on the base line to simulate dampening the string in that place. The harmonics are marked with tallies.
Time Struck:
.43 (3/7)
This is the reason why it has been found advantageous to cover pianoforte hammers with thick layers of felt, rendered elastic by much compression. The outer layers are the softest and most yielding, the lower are firmer. The surface of the hammer comes in contact with the string without any audible impact; the lower layers give the elasticity which throws the hammer back from the string. If you remove a pianoforte hammer and strike it strongly on a wooden table or against a wall, it rebounds from them like an india-rubber ball. The heavier the hammer and the thicker the layers of felt — as in the hammers for the lower octaves — the longer must it be before it rebounds from the string. The hammers for the upper octaves are lighter and have thinner layers of felt. Clearly the makers of these instruments have here been led by practice to discover certain relations of the elasticity of the hammer to the best tones of the string. The make of the hammer has an immense influence on the quality of tone. Theory shews that those upper partial tones are especially favoured whose periodic time is nearly equal to twice the time during which the hammer lies on the string, and that, on the other hand, those disappear whose periodic time is 6, 10, 14, &c., times as great.[19]
It will generally be advantageous, especially for the deeper tones, to eliminate from the series of upper partials, those which lie too close to each other to give a good compound tone, that is, from about the seventh or eighth onwards. Those with higher ordinal numbers are generally relatively weak of themselves. On examining a new grand pianoforte by Messrs. Steinway of New York, which was remarkable for the evenness of its quality of tone, I find that the damping resulting from the duration of the stroke falls, in the deeper notes, on the ninth or tenth partials, whereas in the higher notes, the fourth and fifth partials were scarcely to be got out with the hammer, although they were distinctly audible when the string was plucked by the nail.[20] On the other hand upon an older and much used grand piano, which originally shewed the principal damping in the neighbourhood of the seventh to the fifth partial for middle and low notes, the ninth to the thirteenth partials are now strongly developed. This is probably due to a hardening of the hammers, and certainly can only be prejudicial to the quality of tone. Observations on these relations can be easily made in the method recommended on (p. 52b, c). Put the point of the finger gently on one of the nodes of the tone of which you wish to discover the strength, and then strike the string by means of the digital. By moving the finger till the required tone comes out most purely and sounds the longest, the exact position of the node can be easily found. The nodes which lie near the striking point of the hammer, are of course chiefly covered by the damper, but the corresponding partials are, for a reason to be given presently, relatively weak. Moreover the fifth partial speaks well when the string is touched at two-fifths of its length from the end, and the seventh at two-sevenths of that length. These positions are of course quite free of the damper. Generally we find all the partials which arise from the method of striking used, when we keep on striking while the finger is gradually moved over the length of the string. Touching the shorter end of the string between the striking point and the further bridge will thus bring out the higher partials from the ninth to the sixteenth, which are musically undesirable.
The method of calculating the strength of the individual upper partials, when the duration of the stroke of the hammer is given, will be found further on.
Secondly as to the place struck. In the last chapter, when verifying Ohm’s law for the analysis of musical tones by the ear, we remarked that whether strings are plucked or struck, those upper partials disappear which have a node at the point excited. Conversely; those partials are comparatively strongest which have a maximum displacement at that point. Generally, when the same method of striking is successively applied to different points of a string, the individual upper partials increase or decrease with the intensity of motion, at the point of excitement, for the corresponding simple vibrations of the string. The composition of the musical tone of a string can be consequently greatly varied by merely changing the point of excitement.
Thus if a string be struck in its middle, the second partial tone disappears, because it has a node at that point. But the third partial tone comes out forcibly, because as its nodes lie at \(\tfrac13\) and \(\tfrac23\) the length of the string from its extremities, the string is struck half-way between these two nodes. The fourth partial has its nodes at \(\tfrac14, \tfrac24 (=\tfrac12)\), and \(\tfrac34\) the length of the string from its extremity. It is not heard, because the point of excitement corresponds to its second node. The sixth, eighth, and generally the partials with even numbers disappear in the same way, but the fifth, seventh, ninth, and the other partials with odd numbers are heard. By this disappearance of the evenly numbered partial tones when a string is struck at its middle, the quality of its tone becomes peculiar, and essentially different from that usually heard from strings. It sounds somewhat hollow or nasal. The experiment is easily made on any piano when it is opened and the dampers are raised. The middle of the string is easily found by trying where the finger must be laid to bring out the first upper partial clearly and purely on striking the digital.
If the string is struck at \(\tfrac13\) its length, the third, sixth, ninth, &c., partials vanish. This also gives a certain amount of hollowness, but less than when the string is struck in its middle. When the point of excitement approaches the end of the string, the prominence of the higher upper partials is favoured at the expense of the prime and lower upper partial tones, and the sound of the string becomes poor and tinkling.
In pianofortes, the point struck is about \(\tfrac17\) to \(\tfrac19\) the length of the string from its extremity, for the middle part of the instrument. We must therefore assume that this place has been chosen because experience has shewn it to give the finest musical tone, which is most suitable for harmonies. The selection is not due to theory. It results from attempts to meet the requirements of artistically trained ears, and from the technical experience of two centuries. [21] This gives particular interest to the investigation of the composition of musical tones for this point of excitement. An essential advantage in the choice of this position seems to be that the seventh and ninth partial tones disappear or at least become very weak. These are the first in the series of partial tones which do not belong to the major chord of the prime tone. Up to the sixth partial we have only Octaves, Fifths, and major Thirds of the prime tone; the seventh is nearly a minor Seventh, the ninth a major Second of the prime. Hence these will not fit into the major chord. Experiments on pianofortes shew that when the string is struck by the hammer and touched at its nodes, it is easy to bring out the six first partial tones (at least on the strings of the middle and lower octaves), but that it is either not possible to bring out the seventh, eighth, and ninth at all, or that we obtain at best very weak and imperfect results. The difficulty here is not occasioned by the incapacity of the string to form such short vibrating sections, for if instead of striking the digital we pluck the string nearer to its end, and damp the corresponding nodes, the seventh, eighth, ninth, nay even the tenth and eleventh partial maybe clearly and brightly produced. It is only in the upper octaves that the strings are too short and stiff to form the high upper partial tones. For these, several instrument-makers place the striking point nearer to the extremity, and thus obtain a brighter and more penetrating tone. The upper partials of these strings, which their stiffness renders it difficult to bring out, are thus favoured as against the prime tone. A similarly brighter tone, but at the same time a thinner and poorer one, can be obtained from the lower strings by placing a bridge nearer the striking point, so that the hammer falls at a point less than \(\tfrac17\) of the effective length of the string from its extremity.
While on the one hand the tone can be rendered more tinkling, shrill, and acute, by striking the string with hard bodies, on the other hand it can be rendered duller, that is, the prime tone may be made to outweigh the upper partials, by striking it with a soft and heavy hammer, as, for example, a little iron hammer covered with a thick sheet of india-rubber. The strings of the lower octaves then produce a much fuller but duller tone. To compare the different qualities of tone thus produced by using hammers of different constructions, care must be taken always to strike the string at the same distance from the end as it is struck by the proper hammer of the instrument, as otherwise the results would be mixed up with the changes of quality depending on altering the striking point. These circumstances are of course well known to the instrument-makers, because they have themselves selected heavier and softer hammers for the lower, and lighter and harder for the upper octaves. But when we see that they have not given more than a certain weight to the hammers and have not increased it sufficiently to reduce the intensity of the upper partial tones still further, we feel convinced that a musically trained ear prefers that an instrument to be used for rich combinations of harmony should possess a quality of tone which contains upper partials with a certain amount of strength. In this respect the composition of the tones of pianoforte strings is of great interest for the whole theory of music. In no other instrument is there so wide a field for alteration of quality of tone; in no other, then, was a musical ear so unfettered in the choice of a tone that would meet its wishes.
As I have already observed, the middle and lower octaves of pianoforte strings generally allow the six first partial tones to be clearly produced by striking the digital, and the three first of them are strong, the fifth and sixth distinct, but much weaker. The seventh, eighth, and ninth are eliminated by the position of the striking point. Those higher than the ninth are always very weak. For closer comparison I subjoin a table in which the intensities of the partial tones of a string for different methods of striking have been theoretically calculated from the formula developed in the Appendix V. The effect of the stroke of a hammer depends on the length of time for which it touches the string. This time is given in the table in fractions of the periodic time of the prime tone. To this is added a calculation for strings plucked by the finger. The striking point is always assumed to be at \(\tfrac17\) of the length of the string from its extremity.
|
|
||||||
| Number of the Partial Tone |
|
Struck by a hammer which touches the string for |
|
|||
|
|
|
|
|
|||
| of the periodic time of the prime tone | ||||||
| \(c''\) | \(g'\) | \(C_{\prime}-c'\) | ||||
| 1 | 100 | 100 | 100 | 100 | 100 | 100 |
| 2 | 81.2 | 99.7 | 189.4 | 249 | 285.7 | 324.7 |
| 3 | 56.1 | 8.9 | 107.9 | 242.9 | 357.0 | 504.9 |
| 4 | 31.6 | 2.3 | 17.3 | 118.9 | 259.8 | 504.9 |
| 5 | 13 | 1.2 | 0 | 26.1 | 108.4 | 324.7 |
| 6 | 2.8 | 0.01 | 0.5 | 1.3 | 18.8 | 100.0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 |
For easier comparison the intensity of the prime tone has been throughout assumed as 100. I have compared the calculated intensity of the upper partials with their force on the grand pianoforte already mentioned, and found that the first series, under \(\tfrac37\) suits for about the neighbourhood of \(c''\). In higher parts of the instrument the upper partials were much weaker than in this column. On striking the digital for \(c''\), I obtained a powerful second partial and an almost inaudible third. The second column, marked \(\tfrac{3}{10}\) corresponded nearly to the region of \(g'\), the second and third partials were very strong, the fourth partial was weak. The third column, inscribed \(\tfrac{3}{14}\), corresponds with the deeper tones from \(c'\) downwards; here the four first partials are strong, and the fifth weaker. In the next column, under the third partial tone is stronger than the second; there was no corresponding note on the pianoforte which I examined. With a perfectly hard hammer the third and fourth partials have the same strength, and are stronger than all the others. It results from the calculations in the above table that pianoforte tones in the middle and lower octaves have their fundamental tone weaker than the first, or even than the two first upper partials. This can also be confirmed by a comparison with the effects of plucked strings. For the latter the second partial is weaker than the first; and it will be found that the prime tone is much more distinct in the tones of pianoforte strings when plucked by the finger, than when struck by the hammer.
Although, as is shewn by the mechanism of the upper octaves on pianofortes, it is possible to produce a compound tone in which the prime is predominant, makers have preferred arranging the method of striking the lower strings in such a way as to preserve the five or six first partials distinctly, and to give the second and third greater intensity than the prime.
Thirdly, as regards the thickness and material of the strings. Very rigid strings will not form any very high upper partials, because they cannot readily assume inflections in opposite directions within very short sections. This is easily observed by stretching two strings of different thicknesses on a monochord and endeavouring to produce their high upper partial tones. We always succeed much better with the thinner than with the thicker string. To produce very high upper If partial tones, it is preferable to use strings of extremely fine wire, such as gold lace makers employ, and when they are excited in a suitable manner, as for example by plucking or striking with a metal point, these high upper partials may be heard in the compound itself. The numerous high upper partials which lie close to each other in the scale, give that peculiar high inharmonious noise which we are accustomed to call 'tinkling'. From the eighth partial tone upwards these simple tones are less than a whole Tone apart, and from the fifteenth upwards less than a Semitone. They consequently form a series of dissonant tones. On a string of the finest iron wire, such as is used in the manufacture of artificial flowers, 700 centimetres (22.97 feet) long, I was able to isolate the eighteenth partial tone. The peculiarity of the tones of the zither depends on the presence of these tinkling upper partials, but the series does not extend so far as that just mentioned, because the strings are shorter.
Strings of gut are much lighter than metal strings of the same compactness, and hence produce higher partial tones. The difference of their musical quality depends partly on this circumstance and partly on the inferior elasticity of the gut, which damps their partials, especially their higher partials, much more rapidly. The tone of plucked cat-gut strings (guitar, harp) is consequently much less tinkling than that of metal strings.
No complete mechanical theory can yet be given for the motion of strings excited by the violin-bow, because the mode in which the bow affects the motion of the string is unknown. But by applying a peculiar method of observation, proposed in its essential features by the French physicist Lissajous, I have found it possible to observe the vibrational form of individual points in a violin string, and from this observed form, which is comparatively very simple, to calculate the whole motion of the string and the intensity of the upper partial tones.
Look through a hand magnifying glass consisting of a strong convex lens, at any small bright object, as a grain of starch reflecting a flame, and appearing as a fine point of light. Move the lens about while the point of light remains at rest, and the point itself will appear to move. In the apparatus I have employed, which is shewn in fig. 22 opposite, this lens is fastened to the end of one prong of the tuning-fork G, and marked L. It is in fact a combination of two achromatic lenses, like those used for the object-glasses of microscopes. These two lenses may be used alone as a doublet, or be combined with others. When more magnifying power is required, we can introduce behind the metal plate A A, which carries the fork, the tube and eye-piece of a microscope, of which the doublet then forms the object-glass. This instrument may be called a vibration microscope. When it is so arranged that a fixed luminous point may be clearly seen through it, and the fork is set in vibration, the doublet L moves periodically up and down in pendular vibration. The observer, however, appears to see the luminous point itself vibrate, and, since the separate vibrations succeed each other so rapidly that the impression on the eye cannot die away during the time of a whole vibration, the path of the luminous point appears as a fixed straight line, increasing in length with the excursions of the fork.[22]
The grain of starch which reflects the light to be seen, is then fastened to the resonant body whose vibrations we intend to observe, in such a way that the grain moves backwards and forwards horizontally, while the doublet moves up and down vertically. When both motions take place at once, the observer sees the real horizontal motion of the luminous point combined with its apparent vertical motion, and the combination results in an apparent curvilinear motion. The field of vision in the microscope then shews an apparently steady and unchangeable bright

curve, when either the periodic times of the vibrations of the grain of starch and of the tuning-fork are exactly equal, or one is exactly two or three or four times as great as the other, because in this case the luminous point passes over exactly the same path every one or every two, three, or four vibrations. If these ratios of the vibrational numbers are not exactly perfect, the curves alter slowly, and the effect to the eye is as if they were drawn on the surface of a transparent cylinder which slowly revolved on its axis. This slow displacement of the apparent curves is not disadvantageous, as it allows the observer to see them in different positions. But if the ratio of the pitch numbers of the observed body and of the fork differs too much from one expressible by small whole numbers, the motion of the curve is too rapid for the eye to follow it, and all becomes confusion.
If the vibration microscope has to be used for observing the motion of a violin string, the luminous point must be attached to that string. This is done by first blackening the required spot on the string with ink, and when it is dry, rubbing it over with wax, and powdering this with starch so that a few grains remain sticking. The violin is then fixed with its strings in a vertical direction opposite the microscope, so that the luminous reflection from one of the grains of starch can be clearly seen. The bow is drawn across the strings in a direction parallel to the prongs of the fork. Every point in the string then moves horizontally, and on setting the fork in motion at the same time, the observer sees the peculiar vibrational curves already mentioned. For the purposes of observation I used the \(a'\) string, which I tuned a little higher, as \(b'\flat\), so that it was exactly two Octaves higher than the tuning fork of the microscope, which sounded \(B\flat\).
In fig. 23 are shewn the resulting vibrational curves as seen in the vibration microscope. The straight horizontal lines in the figures, a to a, b to b, c to c
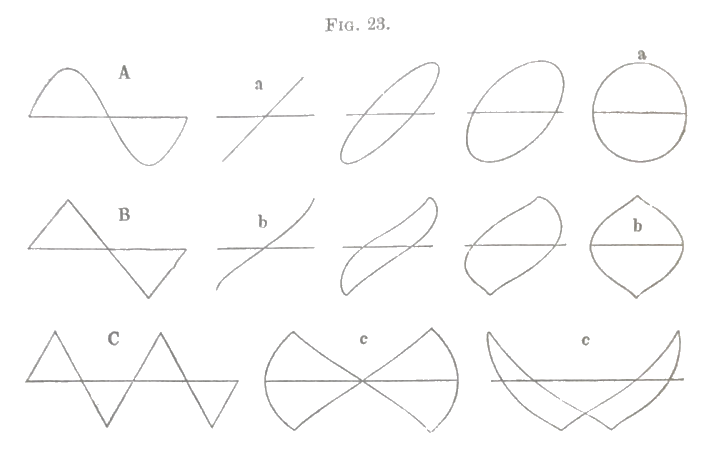
shew the apparent path of the observed luminous point, before it had itself been set in vibration ; the curves and zigzags in the same figures, shew the apparent path of the luminous point when it also was made to move. By their side, in A, B, C, the same vibrational forms are exhibited according to the methods used in Chapters I. and II., the lengths of the horizontal line being directly proportional to the corresponding lengths of time, whereas in figures a to a, b to b, c to c, the horizontal lengths are proportional to the excursions of the vibrating microscope. A, and a to a, shew the vibrational curves for a timing-fork, that is for a simple pendular vibration; B and b to b those of the middle of a violin string in unison with the fork of the vibration microscope; C and c, c, those for a string which was tuned an Octave higher. We may imagine the figures a to a, b to b, and c to c, to be formed from the figures A, B, C, by supposing the surface on which these are drawn to be wrapped round a transparent cylinder whose circumference is of the same length as the horizontal line. The curve drawn upon the surface of the cylinder must then be observed from such a point, that the horizontal line which when wrapped round the cylinder forms a circle, appears perspectively as a single straight line. The vibrational curve A will then appear in the forms a to a, B in the forms b to b, C in the forms c to c. When the pitch of the two vibrating bodies is not in an exact harmonic ratio, this imaginary cylinder on which the vibrational curves are drawn, appears to revolve so that the forms a to a, &c., are assumed in succession.
It is now easy to rediscover the forms A, B, C, from the forms a to a, b to b, and c to c, and as the former give a more intelligible image of the motion of the string than the latter, the curves, which are seen as if they were traced on the surface of a cylinder, will be drawn as if their trace had been unrolled from the cylinder into a plane figure like A, B, C. The meaning of our vibrational curves will then precisely correspond to the similar curves in preceding chapters. When four vibrations of the violin string correspond to one vibration of the fork (as in our experiments, where the fork gave \(B\flat\) and the string \(b'\flat\), p. 82a), so that four waves seem to be traced on the surface of the imaginary cylinder, and when moreover they are made to rotate slowly and are thus viewed in different positions, it is not at all difficult to draw them from immediate inspection as if they had been rolled off on to a plane, for the middle jags have then nearly the same appearance on the cylinder as if they were traced on a plane.
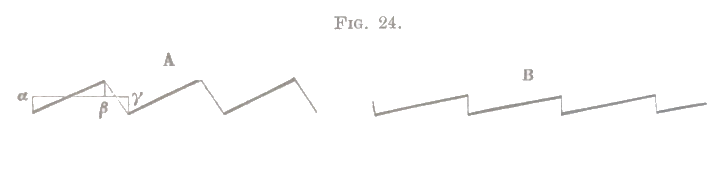
The figures 23 B and 23 C (p. 82b), immediately give the vibrational forms for the middle of a violin string, when the bow bites well, and the prime tone of the string is fully and powerfully produced. It is easily seen that these vibrational forms are essentially different from that of a simple vibration (fig. 23, A). When the point is taken nearer the ends of the string the vibrational figure is shewn in fig. 24, A, and the two sections \(\alpha\beta\), \(\beta\gamma\), of any wave, are to one another as the two sections of the string which lie on either side of the observed point. In the figure
Use the slider to set the location of the peak of the violin wave.
this ratio is 3 : 1, the point being at \(\tfrac14\) the length of the string from its extremity. Close to the end of the string the form is as in fig. 24, B. The short lengths of line in the figure have been made faint because the corresponding motion of the luminous point is so rapid that they often become invisible, and the thicker lengths are alone seen.[23]
These figures shew that every point of the string between its two extremities vibrates with a constant velocity. For the middle point, the velocity of ascent is equal to that of descent. If the violin bow is used near the right end of the string descending, the velocity of descent on the right half of the string is less than that of ascent, and the more so the nearer to the end. On the left half of the string the converse takes place. At the place of bowing the velocity of descent appears to be equal to that of the violin bow. During the greater part of each vibration the string here clings to the bow, and is carried on by it; then it suddenly detaches itself and rebounds, whereupon it is seized by other points in the bow and again carried forward.[24]
Our present purpose is chiefly to determine the upper partial tones. The vibrational forms of the individual points of the string being known, the intensity of each of the partial tones can be completely calculated. The necessary mathematical formulae are developed in Appendix VI. The following is the result of the calculation. When a string excited by a violin bow speaks well, all the upper partial tones which can be formed by a string of its degree of rigidity, are present, and their intensity diminishes as their pitch increases. The amplitude and the intensity of the second partial is one-fourth of that of the prime tone, that of the third partial a ninth, that of the fourth a sixteenth, and so on. This is the same scale of intensity as for the partial tones of a string plucked in its middle, with this exception, that in the latter case the evenly numbered partials all disappear, whereas they are all present when the bow is used. The upper partials in the compound tone of a violin are heard easily and will be found to be strong in sound if they have been first produced as so-called harmonics on the string, by bowing lightly while gently touching a node of the required partial tone. The strings of a violin will allow the harmonics to be produced as high as the sixth partial tone with ease, and with some difficulty even up to the tenth. The lower tones speak best when the string is bowed at from one-tenth to one-twelfth the length of the vibrating portion of the string from its extremity. For the higher harmonics where the sections are smaller, the strings must be bowed at about one-fourth or one-sixth of their vibrating length from the end.[25]
The prime in the compound tones of bowed instruments is comparatively more powerful than in those produced on a pianoforte or guitar by striking or plucking the strings near to their extremities ; the first upper partials are comparatively weaker; but the higher upper partials from the sixth to about the tenth are much more distinct, and give these tones their cutting character.
The fundamental form of the vibrations of a violin string just described, is, when the string speaks well, tolerably independent of the place of bowing, at least in all essential features. It does not in any respect alter, like the vibrational form of struck or plucked strings, according to the position of the point excited. Yet there are certain observable differences of the vibrational figure which depend upon the bowing point. Little crumples are usually perceived on the lines of the vibrational figure, as in fig. 25, which increase in breadth and height the further the bow is removed from the extremity of the string.
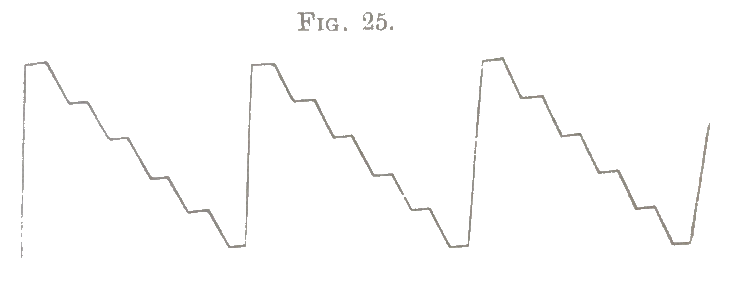
When we bow at a node of one of the higher upper partials which is near the bridge, these crumples are simply reduced by the absence of that part of the normal motion of the string which depends on the partial tones having a node at that place. When the observation on the vibrational form is made at one of the other nodes belonging to the deepest tone which is eliminated, none of these crumples are seen. Thus if the string is bowed at \(\tfrac17\)th, or \(\tfrac67\)ths, or \(\tfrac57\)ths, or \(\tfrac47\)ths, &c., of its length from the bridge, the vibrational figure is simple, as in fig. 24 (p. 83b). But if we observe between two nodes, the crumples appear as in fig. 25. Variations in the quality of tone partly depend upon this condition. When the violin bow is brought too near the finger board, the end of which is \(\tfrac15\)th the length of the string from the bridge, the 5th or 6th partial tone, which is generally distinctly audible, will be absent. The tone is thus rendered duller. The usual place of bowing is at about \(\tfrac{1}{10}\)th of the length of the string; for piano passages it is somewhat further from the bridge and for forte somewhat nearer to it. If the bow is brought near the bridge, and at the same time but lightly pressed, another alteration of quality occurs, which is readily seen on the vibrational figure. A mixture is formed of the prime tone and first harmonic of the string. By light and rapid bowing, namely at about \(\tfrac{1}{20}\)th of the length of the string from the bridge, we sometimes obtain the upper Octave of the prime tone by itself, a node being formed in the middle of the string. On bowing more firmly the prime tone immediately sounds. Intermediately the higher Octave may mix with it in any proportion. This is immediately recognised in the vibrational figure. Fig. 26 gives the corresponding series of forms. It is seen how a fresh crest appears on the longer side of the front of a wave, jutting out at first slightly, then more strongly, till at length the crests of the new waves are as high as those of the old, and then the vibrational number has doubled, and the pitch has passed into the Octave above. The quality of the lowest tone of the string is rendered softer and brighter, but less full and powerful when the intermixture commences. It is interesting to observe the vibrational figure while little changes are made in the style of bowing, and note how the resulting slight changes of quality are immediately rendered evident by very distinct changes in the vibrational figure itself.
This app simulates a bowed string, similar to that on a violin. Click on the base line to simulate dampening the string in that place. The harmonics are marked with tallies.
The vibrational forms just described may be maintained in a uniformly steady and unchanged condition by carefully uniform bowing. The instrument has then an uninterrupted and pure musical quality of tone. Any scratching of the bow is immediately shewn by sudden jumps, or discontinuous displacements and changes in the vibrational figure. If the scratching continues, the eye has no longer time to perceive a regular figure. The scratching noises of a violin bow must therefore be regarded as irregular interruptions of the normal vibrations of the string, making them to recommence from a new starting point. Sudden jumps in the
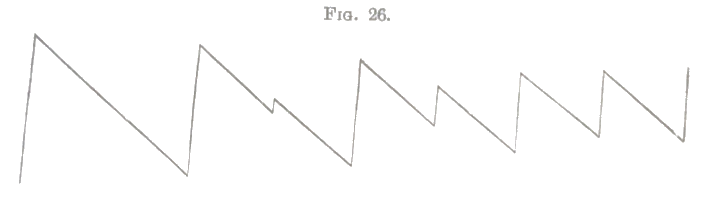
vibrational figure betray every little stumble of the bow which the ear alone would scarcely observe. Inferior bowed instruments seem to be distinguished from good ones by the frequency of such greater or smaller irregularities of vibration. On the string of my monochord, which was only used for the occasion as a bowed instrument, great neatness of bowing was required to preserve a steady vibrational figure lasting long enough for the eye to apprehend it; and the tone was rough in quality, accompanied by much scratching. With a very good modern violin made by Bausch it was easier to maintain the steadiness of the vibrational figure for some time; but I succeeded much better with an old Italian violin of Guadanini, which was the first one on which I could keep the vibrational figure steady enough to count the crumples. This great uniformity of vibration is evidently the reason of the purer tone of these old instruments, since every little irregularity is immediately felt by the ear as a roughness or scratchiness in the quality of tone.
An appropriate structure of the instrument, and wood of the most perfect elasticity procurable, are probably the important conditions for regular vibrations of the string, and when these are present, the bow can be easily made to work uniformly. This allows of a pure flow of tone, undisfigured by any roughness. On the other hand, when the vibrations are so uniform the string can be more vigorously attacked with the bow. Good instruments consequently allow of a much more powerful motion of the string, and the whole intensity of their tone can be communicated to the air without diminution, whereas the friction caused by any imperfection in the elasticity of the wood destroys part of the motion. Much of the advantages of old violins may, however, also depend upon their age, and especially their long use, both of which cannot but act favourably on the elasticity of the wood. But the art of bowing is evidently the most important condition of all. How delicately this must be cultivated to obtain certainty in producing a very perfect quality of tone and its different varieties, cannot be more clearly demonstrated than by the observation of vibrational figures. It is also well known that great players can bring out full tones from even indifferent instruments.
The preceding observations and conclusions refer to the vibrations of the strings of the instrument and the intensity of their upper partial tones, solely in so far as they are contained in the compound vibrational movement of the string. But partial tones of different pitches are not equally well communicated to the air, and hence do not strike the ear of the listener with precisely the same degrees of intensity as those they possess on the string itself. They are communicated to the air by means of the sonorous body of the instrument. As we have had already occasion to remark, vibrating strings do not directly communicate any sensible portion of their motion to the air. The vibrating strings of the violin, in the first place, agitate the bridge over which they are stretched. This stands on two feet over the most mobile part of the 'belly' between the two '\(f\) holes'. One foot of the bridge rests upon a comparatively firm support, namely the 'soundpost,' which is a solid rod inserted between the two plates, back and belly, of the instrument. It is only the other leg which agitates the elastic wooden plates, and through them the included mass of air.[26]
An inclosed mass of air, like that of the violin, vióla, and violoncello, bounded by elastic plates, has certain proper tones which may be evoked by blowing across the openings, or '\(f\) holes'. The violin thus treated gives \(c'\) according to Savart, who examined instruments made by Stradivari (Stradiuarius).[27] Zamminer found the same tone constant on even imperfect instruments. For the violoncello Savart found on blowing over the holes \(F\), and Zamminer \(G\).[28] According to Zamminer the sound-box of the vióla (tenor) is tuned to be a Tone deeper than that of the violin. [29] On placing the ear against the back of a violin and playing a scale on the pianoforte, some tones will be found to penetrate the ear with more force than others, owing to the resonance of the instrument. On a violin made by Bausch two tones of greatest resonance were thus discovered, one between \(c'\) and \(c'\sharp\) [between 264 and 280 vib.], and the other between \(a'\) and \(b'\flat\) [between 440 and 466 vib.]. For a vióla (tenor) I found the two tones about a Tone deeper, which agrees with Zamminer’s calculation.[30]
The consequence of this peculiar relation of resonance is that those tones of the strings which lie near the proper tones of the inclosed body of air, must be proportionably more reinforced. This is clearly perceived on both the violin and violoncello, at least for the lowest proper tone, when the corresponding notes are produced on the strings. They sound particularly full, and the prime tone of these compounds is especially prominent. I think that I heard this also for \(a'\) on the violin, which corresponds to its higher proper tone.
Since the lowest tone on the violin is \(g\), the only upper partials of its musical tones which can be somewhat reinforced by the resonance of the higher proper tone of its inclosed body of air, are the higher octaves of its three deepest notes. But the prime tones of its higher notes will be reinforced more than their upper partials, because these prime tones are more nearly of the same pitch as the proper tones of the body of air. This produces an effect similar to that of the construction of the hammer of a piano, which favours the upper partials of the deep notes, and weakens those of the higher notes. For the violoncello, where the lowest string gives \(C\), the stronger proper tone of the body of air is, as on the violin, a Fourth or a Fifth higher that the pitch of the lowest string. There is consequently a similar relation between the favoured and unfavoured partial tones, but all of them are a Twelfth lower than on the violin. On the other hand, the most favoured partial tones of the vióla (tenor) corresponding nearly with \(b'\), do not lie between the first and second strings, but between the second and third; and this seems to be connected with the altered quality of tone on this instrument. Unfortunately this influence cannot be expressed numerically. The maximum of resonance for the proper tones of the body of air is not very marked; were it otherwise there would be much more inequality in the scale as played on these bowed instruments, immediately on passing the pitch of the proper tones of their bodies of air. We must consequently conjecture that their influence upon the relative intensity of the individual partials in the musical tones of these instruments is not very prominent.

In these instruments the tone is produced by driving a stream of air against an opening, generally furnished with sharp edges, in some hollow space filled with air. To this class belong the bottles described in the last chapter, and shewn in fig. 20 (p. 60c), and especially flutes and the majority of organ pipes. For flutes, the resonant body of air is included in its own cylindrical bore. It is blown with the mouth, which directs the breath against the somewhat sharpened edges of its mouth hole. The construction of organ pipes will be seen from the two adjacent figures. Fig. 27, A, shews a square wooden pipe, cut open longwise, and B the external appearance of a round tin pipe. R R in each shews the tube which incloses the sonorous body of air, a b is the mouth where it is blown, terminating in a sharp lip. In fig. 27, A, we see the air chamber or throat K into which the air is first driven from the bellows, and whence it can only escape through the narrow slit c d, which directs it against the edge of the lip. The wooden pipe A as here drawn is open, that is its extremity is uncovered, and it produces a tone with a wave of air twice as long as the tube R R. The other pipe, B, is stopped, that is, its upper extremity is closed. Its tone has a wave four times the length of the tube R R, and hence an Octave deeper than an open pipe of the same length.[31]
Any air chambers can be made to give a musical tone, just like organ pipes, flutes, the bottles previously described, the windchests of violins, &c., provided they have a sufficiently narrow opening, furnished with somewhat projecting sharp edges, by directing a thin flat stream of air across the opening and against its edges.[32]
The motion of air that takes place in the inside of organ pipes, corresponds to a system of plane waves which are reflected backwards and forwards between the two ends of the pipe. At the stopped end of a cylindrical pipe the reflexion of every wave that strikes it is very perfect, so that the reflected wave has the same intensity as it had before reflexion. In any train of waves moving in a given direction, the velocity of the oscillating molecules in the condensed portion of the wave takes place in the same direction as that of the propagation of the waves, and in the rarefied portion in the opposite direction. But at the stopped end of a pipe its cover does not allow of any forward motion of the molecules of air in the direction of the length of the pipe. Hence the incident and reflected wave at this place combine so as to excite opposite velocities of oscillation of the molecules of air, and consequently by their superposition the velocity of the molecules of air at the cover is destroyed. Hence it follows that the phases of pressure in both will agree, because opposite motions of oscillation and opposite propagation, result in accordant pressure.
Hence at the stopped end there is no motion, but great alteration of pressure. The reflexion of the wave takes place in such a manner that the phase of condensation remains unaltered, but the direction of the motion of oscillation is reversed.
The contrary takes place at the open end of pipes, in which is also included the opening of their mouths. At an open end where the air of the pipe communicates freely with the great outer mass of air, no sensible condensation can take place. In the explanation usually given of the motion of air in pipes, it is assumed that both condensation and rarefaction vanish at the open ends of pipes, which is approximately but not exactly correct. If there were exactly no alteration of density at that place, there would be complete reflexion of every incident wave at the open ends, so that an equally large reflected wave would be generated with an opposite state of density, but the direction of oscillation of the molecules of air in both waves would agree. The superposition of such an incident and such a reflected wave would indeed leave the state of density unaltered at the open ends, but would occasion great velocity in the oscillating molecules of air.
In reality the assumption made explains the essential phenomena of organ pipes. Consider first a pipe with two open ends. On our exciting a wave of condensation at one end, it runs forward to the other end, is there reflected as a wave of rarefaction, runs back to the first end, is here again reflected with another alteration of phase, as a wave of condensation, and then repeats the same path in the same way a second time. This repetition of the same process therefore occurs, after the wave in the tube has passed once forwards and once backwards, that is twice through the whole length of the tube. The time required to do this is equal to double the length of the pipe divided by the velocity of sound. This is the duration of the vibration of the deepest tone which the pipe can give.
Suppose now that at the time when the wave begins its second forward and backward journey, a second impulse in the same direction is given, say by a vibrating tuning-fork. The motion of the air will then receive a reinforcement, which will constantly increase, if the fresh impulses take place in the same rhythm as the forward and backward progression of the waves.
Even if the returning wave does not coincide with the first following similar impulse of the tuning-fork, but only with the second or third or fourth and so on, the motion of the air will be reinforced after every forward and backward passage.
A tube open at both ends will therefore serve as a resonator for tones whose pitch number is equal to the velocity of sound (332 metres)[33] divided by twice the length of the tube, or some multiple of that number. That is to say, the tones of strongest resonance for such a tube will, as in strings, form the complete series of harmonic upper partials of its prime.
The case is somewhat different for pipes stopped at one end. If at the open end, by means of a vibrating tuning-fork, we excite an impulse of condensation which propagates itself along the tube, it will run on to the stopped end, will be there reflected as a wave of condensation, return, will be again reflected at the open end with altered phase as a wave of rarefaction, and only after it has been again reflected at the stopped end with a similar phase, and then, once more at the open end with an altered phase as a condensation, will a repetition of the process ensue, that is to say, not till after it has traversed the length of the pipe four times. Hence the prime tone of a stopped pipe has twice as long a period of vibration as an open pipe of the same length. That is to say, the stopped pipe will be an Octave deeper than the open pipe. If, then, after this double forward and backward passage, the first impulse is renewed, there will arise a reinforcement of resonance.
Partials [34] of the prime tone can also be reinforced, but only those which are unevenly numbered. For since at the expiration of half the period of vibration, the prime tone of the wave in the tube renews its path with an opposite phase of density, only such tones can be reinforced as have an opposite phase at the expiration of half the period of vibration. But at this time the second partial has just completed a whole vibration, the fourth partial two whole vibrations, and so on. These therefore have the same phases, and cancel their effect on the return of the wave with an opposite phase. Hence the tones of strongest resonance in stopped pipes correspond with the series of unevenly numbered partials of its fundamental tone. Supposing its pitch number is \(n\), then \(3n\) is the Twelfth of \(n\), that is the Fifth of \(2n\) the higher Octave, and \(5n\) is the major Third of \(4n\) the next higher Octave, and \(7n\) the [sub] minor Seventh of the same Octave, and so on.
Now although the phenomena follow these rules in the principal points, certain deviations from them occur because there is not precisely no change of pressure at the open ends of pipes. From these ends the motion of sound communicates itself to the uninclosed air beyond, and the waves which spread out from the open ends of the tubes have relatively very little alteration of pressure, but are not entirely without some. Hence a part of every wave which is incident on the open end of the pipe is not reflected, but runs out into the open air, while the remainder or greater portion of the wave is reflected, and returns into the tube. The reflexion is the more complete, the smaller are the dimensions of the opening of the tube in comparison with the wave-length of the tone in question.
Theory[35]also, agreeing with experiment, shews that the phases of the reflected part of the wave are the same as they would be if the reflexion did not take place at the surface of the opening itself but at another and somewhat different plane. Hence what may be called the reduced length of the pipe, or that answering to the pitch, is somewhat different from the real length, and the difference between the two depends on the form of the mouth, and not on the pitch of the notes produced unless they are so high and hence their wave-lengths so short, that the dimensions of the opening cannot be neglected in respect to them.
For cylindrical pipes of circular section, with ends cut at right angles to the length, the distance of the plane of reflexion from the end of the pipe is theoretically determined to be at a distance of 0.7854 the radius of the circle.[36] For a wooden pipe of square section, of which the sides were 36 mm. (1-4 inch) internal measure, I found the distance of the plane of reflexion 14 mm. (.55 inch). [37]
Now since on account of the imperfect reflexion of waves at the open ends of organ pipes (and respectively at their mouths) a part of the motion of the air must escape into the free air at every vibration, any oscillatory motion of its mass of air must be speedily exhausted, if there are no forces to replace the lost motion. In fact, on ceasing to blow an organ pipe scarcely any after sound is observable. Nevertheless the wave is frequently enough reflected forward and backward for its pitch to become perceptible on tapping against the pipe.
The means usually adopted for keeping them continually sounding, is blowing. In order to understand the action of this process, we must remember that when air is blown out of such a slit as that which lies below the lip of the pipe, it breaks through the air which lies at rest in front of the slit in a thin sheet like a blade or lamina, and hence at first does not draw any sensible part of that air into its own motion. It is not till it reaches a distance of some centimetres [a centimetre is nearly four-tenths of an inch] that the outpouring sheet splits up into eddies or vortices, which effect a mixture of the air at rest and the air in motion. This blade-shaped sheet of air in motion can be rendered visible by sending a stream of air impregnated with smoke or clouds of salammoniac through the mouth of a pipe from which the pipe itself is removed, such as is commonly found among physical apparatus. Any blade-shaped gas flame which comes from a split burner is also an example of a similar process. Burning renders visible the limits between the outpouring sheet of gas and the atmosphere. But the flame does not render the continuation of the stream visible.
Now the blade-shaped sheet of air at the mouth of the organ pipe is wafted to one side or the other by every stream of air which touches its surface, exactly as this gas flame is. The consequence is that when the oscillation of the mass of air in the pipe[38] causes the air to enter through the ends of the pipe, the blade-shaped stream of air arising from the mouth is also inclined inwards, and drives its whole mass of air into the pipe.[39] During the opposite phase of vibration, on the other hand, when the air leaves the ends of the pipe the whole mass of this blade of air is driven outwards. Hence it happens that exactly at the times when the air in the pipe is most condensed, more air still is driven in from the bellows, whence the condensation, and consequently also the equivalent of work of the vibration of the air is increased, while at the periods of rarefaction in the pipe the wind of the bellows pours its mass of air into the open space in front of the pipe. We must remember also that the blade-shaped sheet of air requires time in order to traverse the width of the mouth of the pipe, and is during this time exposed to the action of the vibrating column of air in the pipe, and does not reach the lip (that is the line where the two paths, inwards and outwards, intersect) until the end of this time. Every particle of air that is blown in, consequently reaches a phase of vibration in the interior of the pipe, which is somewhat later than that to which it was exposed in traversing the opening. If the latter motion was inwards, it encounters the following condensation in the interior of the pipe, and so on.
This mode of exciting the tone conditions also the peculiar quality of tone of these organ pipes. We may regard the blade-shaped stream of air as very thin in comparison with the amplitude of the vibrations of air. The latter often amount to 10 or 16 millimetres (.39 to .63 inches), as may be seen by bringing small flames of gas close to this opening. Consequently the alternation between the periods of time for which the whole blast is poured into the interior of the pipe, and those for which it is entirely emptied outside, is rather sudden, in fact almost instantaneous. Hence it follows [40] that the oscillations excited by blowing are of a similar kind; namely, that for a certain part of each vibration the velocity of the particles of air in the mouth and in free space, have a constant value directed outwards, and for a second portion of the same, a constant value directed inwards. With stronger blowing that directed inwards will be more intense and of shorter duration ; with weaker blowing, the converse may take place. Moreover, the pressure in the mass of air put in motion in the pipe must also alternate between two constant values with considerable rapidity. The rapidity of this change will, however, be moderated by the circumstance that the blade-shaped sheet of air is not infinitely thin, but requires a short time to pass over the lip of the pipe, and that secondly the higher upper partials, whose wave-lengths only slightly exceed the diameter of the pipe, are as a general rule imperfectly developed.
The kind of motion of the air here described is exactly the same as that shewn in fig. 23 (p. 82b), B and C, fig. 24 (p. 83b), A and B, for the vibrating points of a violin string. Organ-builders have long since remarked the similarity of the quality of tone, for the narrower cylindrical-pipe stops when strongly blown, as shewn by the names: Geigenprincipal, Vifila di Gamba, Violoncello, Violon-bass.[41] That these conclusions from the mechanics of blowing correspond with the facts in nature, is shewn by the experiments of Messrs. Toepier & Boltzmann, [42] who rendered the form of the oscillation of pressure in the interior of the pipe optically observable by the interference of light passed through a node of the vibrating mass of air. When the force of the wind was small they found almost a simple vibration (the smaller the oscillation of the air-blade at the lip, the more completely the discontinuities disappear). But when the force of the wind was greater they found a very rapid alternation between two different values of pressure, each of which remained almost unaltered for a fraction of a vibration.
Messrs. Mach and J. Hervert’s [43] experiments with gas flames placed before the end of an open pipe to make the vibrations visible, shew that the form of motion just described really occurs at the ends of the pipes. The forms of vibration which they deduced from the analysis of the forms of the flames correspond with those of a violin string, except that, for the reason given above, their corners are rounded off.
By using resonators I find that on narrow pipes of this kind the partial tones may be clearly heard up to the sixth.
For wide open pipes, on the other hand, the adjacent proper tones of the tube are all somewhat sharper than the corresponding harmonic tones of the prime, and hence these tones will be much less reinforced by the resonance of the tube. Wide pipes, having larger masses of vibrating air and admitting of being much more strongly blown without jumping up into an harmonic, are used for the great body of sound on the organ, and are hence called principalstimmen.[44] For the above reasons they produce the prime tone alone strongly and fully, with a much weaker retinue of secondary tones. For wooden 'principal' pipes, I find the prime tone and its Octave or first upper partial very distinct; the Twelfth or second upper partial is but weak, and the higher upper partials no longer distinctly perceptible. For metal pipes the fourth partial was also still perceptible. The quality of tone in these pipes is fuller and softer than that of the geigenprincipal. When flute or flue stops of the organ, and the German flute are blown softly, the upper partials lose strength at a greater rate than the prime tone, and hence the musical quality becomes weak and soft.
Another variety is observed on the pipes which are conically narrowed at their upper end, in the salicional, gemshorn, and spitzflöte stops.[45] Their upper opening has generally half the diameter of the lower section; for the same length the salicional pipe has the narrowest, and the spitzflöte the widest section. These pipes have, I find, the property of rendering some higher partial tones, from the Fifth to the Seventh, comparatively stronger than the lower. The quality of tone is consequently poor but peculiarly bright.
The narrower stopped cylindrical pipes have proper tones corresponding to the unevenly numbered partials of the prime, that is, the third partial or Twelfth, the fifth partial or higher major Third, and so on. For the wider stopped pipes, as for the wide open pipes, the next adjacent proper tones of the mass of air are distinctly higher than the corresponding upper partials of the prime, and consequently these upper partials are very slightly, if at all, reinforced. Hence wide stopped pipes, especially when gently blown, give the prime tone almost alone, and they were therefore previously adduced as examples of simple tones (p. 60c). Narrow stopped pipes, on the other hand, let the Twelfth be very distinctly heard at the same time with the prime time; and have hence been called quintaten (quintam tenentes).[46] When these pipes are strongly blown they also give the fifth partial, or higher major Third, very distinctly. Another variety of quality is produced by the rohrflöte.[47] Here a tube, open at both ends, is inserted in the cover of a stopped pipe, and in the examples I examined, its length was that of an open pipe giving the fifth partial tone of the prime tone of the stopped pipe. The fifth partial tone is thus proportionably stronger than the rather weak third partial on these pipes, and the quality of tone becomes peculiarly bright. Compared with open pipes the quality of tone in stopped pipes, where the evenly numbered partial tones are absent, is somewhat hollow; the wider stopped pipes have a dull quality of tone, especially when deep, and are soft and powerless. But their softness offers a very effective contrast to the more cutting qualities of the narrower open pipes and the noisy compound stops, of which I have already spoken (p. 57b), and which, as is well known, form a compound tone by uniting many pipes corresponding to a prime and its upper partial tones.
Wooden pipes do not produce such a cutting windrush as metal pipes. Wooden sides also do not resist the agitation of the waves of sound so well as metal ones, and hence the vibrations of higher pitch seem to be destroyed by friction. For these reasons wood gives a softer, but duller, less penetrating quality of tone than metal.
It is characteristic of all pipes of this kind that they speak readily, and hence admit of great rapidity in musical divisions and figures, but, as a little increase of force in blowing distinctly alters the pitch, their loudness of tone can scarcely be changed. Hence on the organ forte and piano have to be produced by stops, which regulate the introduction of pipes with various qualities of tone, sometimes more, sometimes fewer, now the loud and cutting, now the weak and soft. The means of expression on this instrument are therefore somewhat limited, but, on the other hand, it clearly owes part of its magnificent properties to its power of sustaining tones with unaltered force, undisturbed by subjective excitement.
The mode of producing the tones on these instruments resembles that used for the siren: the passage for the air being alternately closed and opened, its stream is separated into a series of individual pulses. This is effected on the siren, as we have already seen, by means of a rotating disc pierced with holes. In reed instruments, elastic plates or tongues are employed which are set in vibration and thus alternately close and open the aperture in which they are fastened. To these belong —

1. The reed pipes of organs and the vibrators of harmoniums. Their tongues, shewn in perspective in fig. 28, A, and in section in fig. 28, B, are thin oblong metal plates, z z, fastened to a brass block, a a, in which there is a hole, b b, behind the tongue and of the same shape. When the tongue is in its position of rest, it closes the hole completely, with the exception of a very fine chink all round its margin. When in motion it oscillates between the positions marked z\(_1\) and z\(_2\) in fig. 28, B. In the position z\(_1\) there is an aperture for the stream of air to enter, in the direction shewn by the arrow, and this is closed when the tongue has reached the other extreme position z\(_2\) The tongue shewn is a free vibrator or anche libre, such as is now universally employed. These tongues are slightly smaller than the corresponding opening, so that they can bend inwards without touching the edges of the hole.[48] Formerly, striking vibrators or reeds were employed, which on each oscillation struck against their frame. But as these produced a harsh quality of tone and an uncertain pitch they have gone out of use.[49]
The mode in which tongues are fastened in the reed stops of organs is shewn in fig. 29, A and B below. A bears a resonant cup above; B is a longitudinal section; p p is the air chamber into which the wind is driven; the tongue l is fastened in the groove r, which fits into the block s; d is the tuning wire, which presses against the tongue, and being pushed down shortens it and hence sharpens its pitch, and, conversely, flattens the pitch when pulled up. Slight variations of pitch are thus easily produced.[50]

2. The tongues of clarinets, oboes, and bassoons, are constructed in a somewhat similar manner and are cut out of elastic reed plates. The clarinet has a single wide tongue which is fastened before the corresponding opening of the mouthpiece like the metal tongues previously described, and would strike the frame if its excursions were long enough. But its excursions are small, and the pressure of the lips brings it just near enough to make the chink sufficiently small without allowing it to strike. For the oboe and bassoon two reeds or tongues of the same kind are placed opposite each other at the end of the mouthpiece. They are separated by a narrow chink, and by blowing are pressed near enough to close the chink whenever they swing inwards.
3. Membranous tongues. — The peculiarities of these tongues are best studied on those artificially constructed.

Cut the end of a wooden or gutta-percha tube obliquely on both sides, as shewn in fig. 30, leaving two nearly rectangular points standing between the two edges which are cut obliquely. Then gently stretch strips of vulcanised india-rubber over the two oblique edges, so as to leave a small slit between them, and fasten them with a thread. A reed mouthpiece is thus constructed which may be connected in any way with tubes or other air chambers. When the membranes bend inwards the slit is closed; when outwards, it is open. Membranes which are fastened in this oblique manner speak much better than those which are laid at right angles to the axis of the tube, as Johannes Muller proposed, for in the latter case they require to be bent outwards by the air before they can begin to open and shut alternately. Membranous tongues of the kind proposed may be blown either in the direction of the arrows or in the opposite direction. In the first case they open the slit when they move towards the air chamber, that is, towards the further end of the conducting tube. Tongues of this kind I distinguish as striking inwards. When blown they always give deeper tones than they would do if allowed to vibrate freely, that is, without being connected with an air chamber. The tongues of organ pipes, harmoniums, and wooden wind instruments already mentioned, are likewise always arranged to strike inwards. But both membranous and metal tongues may be arranged so as to act against the stream of air, and hence to open when they move towards the outer opening of the instrument. I then say that they strike outwards. The tones of tongues which strike outwards are always sharper than those of isolated tongues.
Only two kinds of membranous tongues have to be considered as musical instruments: the human lips in brass instruments, and the human larynx in singing.
The lips must be considered as very slightly elastic membranous tongues, loaded with much inelastic tissue containing water, and they would consequently vibrate very slowly, if they could be brought to vibrate by themselves. In brass instruments they form membranous tongues which strike outwards, and consequently by the above rule produce tones sharper than their proper tones. But as they offer very slight resistance, they are readily set in motion, by the alternate pressure of the vibrating column of air, when used with brass instruments.[51]
In the larynx, the elastic vocal chords act as membranous tongues. They are stretched across the windpipe, from front to back, like the india-rubber strips in fig. 30 (p. 97a), and leave a small slit, the glottis, between them. They have the advantage over all artificially constructed tongues of allowing the width of their slit, their tension, and even their form to be altered at pleasure with extraordinary rapidity and certainty, at the same time that the resonant tube formed by the opening of the mouth admits of much variety of form, so that many more qualities of tone can be thus produced than on any instrument of artificial construction. If the vocal chords are examined from above with a laryngoscope, while producing a tone, they will be seen to make very large vibrations for the deeper breast voice, shutting the glottis tightly whenever they strike inwards.
The pitch of the various reeds or tongues just mentioned is altered in very different manners. The metal tongues of the organ and harmonium are always intended to produce one single tone apiece. On the motion of these comparatively heavy and stiff tongues, the pressure of the vibrating air has very small influence, and their pitch within the instrument is consequently not much different from that of the isolated tongues. There must be at least one tongue for each note on such instruments.
In wooden wind instruments, a single tongue has to serve for the whole series of notes. But the tongues of these instruments are made of light elastic wood, which is easily set in motion by the alternating pressure of the vibrating column of air, arid swings sympathetically with it. Such instruments, therefore, in addition to those very high tones, which nearly correspond to the proper tones of their tongues, can, as theory and experience alike shew, also produce deep tones of a very different pitch,[52] because the waves of air which arise in the tube of the instrument excite an alternation in the pressure of air adjacent to the tongue itself sufficiently powerful to make it vibrate sensibly. Now in a vibrating column of air the alteration of pressure is greatest where the velocity of the particles of air is smallest; and since the velocity is always null, that is a minimum, at the end of a closed tube, such as a stopped organ pipe, and the alteration of pressure in that place is consequently a maximum, the tones of these reed pipes must be the same as those which the resonant tube alone would produce, if it were stopped at the place where the tongue is placed, and were blown as a stopped pipe. In musical practice, then, such tones of the instrument as correspond to the proper tones of the tongue are not used at all, because they are very high and screaming, and their pitch cannot be preserved with sufficient steadiness when the tongue is wet. The only tones produced are considerably deeper than the proper tone of the tongue, and have their pitches determined by the length of the column of air, which corresponds to the proper tones of the stopped pipe.
The clarinet has a cylindrical tube, the proper tones of which correspond to the third, fifth, seventh, &c., partial tone of the prime. By altering the style of blowing, it is possible to pass from the prime to the Twelfth or the higher major Third. The acoustic length of the tube may also be altered by opening the side holes of the clarinet, in which case the vibrating column of air is principally that between the mouthpiece and the uppermost open side hole.[53]
The oboe (hautbois) and bassoon (fagotto) have conical tubes which are closed up to the vertex of their cone, and have proper tones that are the same as those of open tubes of the same length. Hence the tones of both of these instruments nearly correspond to those of open pipes. By overblowing they give the Octave, Twelfth, second Octave, and so on, of the prime tone. Intermediate tones are produced by opening side holes.
The older \(horns\) and \(trumpets\) consist of long conical bent tubes, without keys or side holes.[54] They can produce such tones only as correspond to the proper tones of the tube, and these again are the natural harmonic upper partials of the prime. But as the prime tone of such a long tube is very deep, the upper partial tones in the middle parts of the scale lie rather close together, especially in the extremely long tubes of the horn,[55] so that they give most of the degrees of the scale. The trumpet is restricted to these natural tones. But by introducing the hand into the bell of the French horn and thus partly closing it, and by lengthening the tube of the trombone,[56] it was possible in some degree to supply the missing tones and improve the faulty ones. In later times trumpets and horns have been frequently supplied with keys [57] to supply the missing tones, but at some expense of power in the tone and the brilliancy in its quality. The vibrations of the air in these instruments are unusually powerful, and require the resistance of firm, smooth, unbroken tubes to preserve their strength. In the use of brass instruments, the different form and tension of the lips of the player act only to determine which of the proper tones of the tube shall speak; the pitch of the individual tones is almost [58] entirely independent of the tension of the lips.
On the other hand, in the larynx the tension of the vocal chords, which here form the membranous tongues, is itself variable, and determines the pitch of the tone. The air chambers connected with the larynx are not adapted for materially altering the tone of the vocal chords. Their walls are so yielding that they cannot allow the formation of vibrations of the air within them sufficiently powerful to force the vocal chords to oscillate with a period which is different from that required by their own elasticity. The cavity of the mouth is also far too short, and generally too widely open for its mass of air to have material influence on the pitch.
In addition to the tension of the vocal chords (which can be increased not only by separating the points of their insertion in the cartilages of the larynx, but also by voluntarily stretching the muscular fibres within them), their thickness seems also to be variable. Much soft watery inelastic tissue lies underneath the elastic fibrils proper and the muscular fibres of the vocal chords, and in the breast voice this probably acts to weight them and retard their vibrations. The head voice is probably produced by drawing aside the mucous coat below the chords, thus rendering the edge of the chords sharper, and the weight of the vibrating part less, while the elasticity is unaltered.[59]
We now proceed to investigate the quality of tone produced on reed pipes, which is our proper subject. The sound in these pipes is excited by intermittent pulses of air, which at each swing break through the opening that is closed by the tongue of the reed. A freely vibrating tongue has far too small a surface to communicate any appreciable quantity of sonorous motion to the surrounding air; and it is as little able to excite the air inclosed in pipes. The sound seems to be really produced by pulses of air, as in the siren, where the metal plate that opens and closes the orifice does not vibrate at all. By the alternate opening and closing of a passage, a continuous influx of air is changed into a periodic motion, capable of affecting the air. Like any other periodic motion of the air, the one thus produced can also be resolved into a series of simple vibrations. We have already remarked that the number of terms in such a series will increase with the discontinuity of the motion to be thus resolved (p. 34d). Now the motion of the air which passes through a siren, or past a vibrating tongue, is discontinuous in a very high degree, since the individual pulses of air must be generally separated by complete pauses during the closures of the opening. Free tongues without a resonance tube, in which all the individual simple tones of the vibration which they excite in the air are given off freely to the surrounding atmosphere, have consequently always a very sharp, cutting, jarring quality of tone, and we can really hear with either armed or unarmed ears a long series of strong and clear partial tones up to the 16th or 20th, and there are evidently still higher partials present, although it is difficult or impossible to distinguish them from each other, because they do not lie so much as a Semitone apart.[60] This whirring of dissonant partial tones makes the musical quality of free tongues very disagreeable.[61] A tone thus produced also shews that it is really due to puffs of air. I have examined the vibrating tongue of a reed pipe, like that in fig. 28 (p. 95b), when in action with the vibration microscope of Lissajous, in order to determine the vibrational form of the tongue, and I found that the tongue performed perfectly regular simple vibrations. Hence it would communicate to the air merely a simple tone and not a compound tone, if the sound were directly produced by its own vibrations.
The intensity of the upper partial tones of a free tongue, unconnected with a resonance tube, and their relation to the prime, are greatly dependent on the nature of the tongue, its position with respect to its frame, the tightness with which it closes, &c. Striking tongues which produce the most discontinuous pulses of air, also produce the most cutting quality of tone.[62] The shorter the puff of air, and hence the more sudden its action, the greater number of high upper partials should we expect, exactly as we find in the siren, according to Seebeck’s investigations. Hard, unyielding material, like that of brass tongues, will produce pulses of air which are much more disconnected than those formed by soft and yielding substances. This is probably the reason why the singing tones of the human voice are softer than all others which are produced by reed pipes. Nevertheless the number of upper partial tones in the human voice, when used in emphatic forte, is very great, and they reach distinctly and powerfully up to the four-times accented [or quarter-foot] Octave (p. 26a). To this we shall have to return.
The tones of tongues are essentially changed by the addition of resonance tubes, because they reinforce and hence give prominence to those upper partial tones which correspond to the proper tones of these tubes.[63] In this case the resonance tubes must be considered as closed at the point where the tongue is inserted.[64]
A brass tongue such as is used in organs, and tuned to \(b\flat\), was applied to one of my larger spherical resonators, also tuned to \(b\flat\), instead of to its usual resonance tube. After considerably increasing the pressure of wind in the bellows, the tongue spoke somewhat flatter than usual, but with an extraordinarily full, beautiful, soft tone, from which almost all upper partials were absent. Very little wind was used, but it was under high pressure. In this case the prime tone of the compound was in unison with the resonator, which gave a powerful resonance, and consequently the prime tone had also great power. None of the higher partial tones could be reinforced. The theory of the vibrations of air in the sphere further shews that the greatest pressure must occur in the sphere at the moment that the tongue opens. Hence arose the necessity of strong pressure in the bellows to overcome the increased pressure in the sphere, and yet not much wind really passed.
If instead of a glass sphere, resonant tubes are employed, which admit of a greater number of proper tones, the resulting musical tones are more complex. In the clarinet we have a cylindrical tube which by its resonance reinforces the uneven partial tones. [65] The conical tubes of the oboe, bassoon, trumpet, and French horn, on the other hand, reinforce all the harmonic upper partial tones of the compound up to a certain height, determined by the incapacity of the tubes to resound for waves of sound that are not much longer than the width of the opening. By actual trial I found only unevenly numbered partial tones, distinct to the seventh inclusive, in the notes of the clarinet, whereas on other instruments, which have conical tubes, I found the evenly numbered partials also. I have not yet had an opportunity of making observations on the further differences of quality in the tones of individual instruments with conical tubes. This opens rather a wide field for research, since the quality of tone is altered in many ways by the style of blowing, and even on the same instrument the different parts of the scale, when they require the opening of side holes, shew considerable differences in quality. On wooden wind instruments these differences are striking. The opening of side holes is by no means a complete substitute for shortening the tube, and the reflection of the waves of sound at the points of opening is not the same as at the free open end of the tube. The upper partials of compound tones produced by a tube limited by an open side hole, must certainly be in general materially deficient in harmonic purity, and this will also have a marked influence on their resonance.[66]
We have hitherto discussed cases of resonance, generated in such air chambers as were capable of reinforcing the prime tone principally, but also a certain number of the harmonic upper partial tones of the compound tone produced. The case, however, may also occur in which the lowest tone of the resonance chamber applied does not correspond with the prime, but only with some one of the upper partials of the compound tone itself, and in these cases we find, in accordance with the principles hitherto developed, that the corresponding upper partial tone is really more reinforced than the prime or other partials by the resonance of the chamber, and consequently predominates extremely over all the other partials in the series. The quality of tone thus produced has consequently a peculiar character, and more or less resembles one of the vowels of the human voice. For the vowels of speech are in reality tones produced by membranous tongues (the vocal chords), with a resonance chamber (the mouth) capable of altering in length, width, and pitch of resonance, and hence capable also of reinforcing at different times different partials of the compound tone to which it is applied.[67]
In order to understand the composition of vowel tones, we must in the first place bear in mind that the source of their sound lies in the vocal chords, and that when the voice is heard, these chords act as membranous tongues, and like all tongues produce a series of decidedly discontinuous and sharply separated pulses of air, which, on being represented as a sum of simple vibrations, must consist of a very large number of them, and hence be received by the ear as a very long series of partials belonging to a compound musical tone. With the assistance of resonators it is possible to recognise very high partials, up to the sixteenth, when one of the brighter vowels is sung by a powerful bass voice at a low pitch, and, in the case of a strained forte in the upper notes of any human voice, we can hear, more clearly than on any other musical instrument, those high upper partials that belong to the middle of the four-times accented Octave (the highest on modern pianofortes, see note 14, p. 18d), and these high tones have a peculiar relation to the ear, to be subsequently considered. The loudness of such upper partials, especially those of highest pitch, differs considerably in different individuals. For cutting bright voices it is greater than for soft and dull ones. The quality of tone in cutting screaming voices may perhaps be referred to a want of sufficient smoothness or straightness in the edges of the vocal chords, to enable them to close in a straight narrow slit without striking one another. This circumstance would give the larynx more the character of striking tongues, and the latter have a much more cutting quality than the free tongues of the normal vocal chords. Hoarseness in voices may arise from the glottis not entirely closing during the vibrations of the vocal chords. At any rate, when alterations of this kind are made in artificial membranous tongues, similar results ensue. For a strong and yet soft quality of voice it is necessary that the vocal chords should, even when most strongly vibrating, join rectilinearly at the moment of approach with perfect tightness, effectually closing the glottis for the moment, but without overlapping or striking against each other. If they do not close perfectly, the stream of air will not be completely interrupted, and the tone cannot be powerful. If they overlap, the tone must be cutting, as before remarked, as those arising from striking tongues. On examining the vocal chords in action by means of a laryngoscope, it is marvellous to observe the accuracy with which they close even when making vibrations occupying nearly the entire breadth of the chords themselves.[68]
There is also a certain difference in the way of putting on the voice in speaking and in singing, which gives the speaking voice a much more cutting quality of tone, especially in the open vowels, and occasions a sensation of much greater pressure in the larynx. I suspect that in speaking the vocal chords act as striking tongues.[69]
When the mucous membrane of the larynx is affected with catarrh, the laryngoscope sometimes shews little flakes of mucus in the glottis. When these are too great they disturb the motion of the vibrating chords and make them irregular, causing the tone to become unequal, jarring, or hoarse. It is, however, remarkable what comparatively large flakes of mucus may lie in the glottis without producing a very striking deterioration in the quality of tone.
It has already been mentioned that it is generally more difficult for the unassisted ear to recognise the upper partials in the human voice, than in the tones of musical instruments. Resonators are more necessary for this examination than for the analysis of any other kind of musical tone. The upper partials of the human voice have nevertheless been heard at times by attentive observers. Rameau had heard them at the beginning of last century. And at a later period Seiler of Leipzig relates that while listening to the chant of the watchman during a sleepless night, he occasionally heard at first, when the watchman was at a distance, the Twelfth of the melody, and afterwards the prime tone. The reason of this difficulty is most probably that we have all our lives remarked and observed the tones of the human voice more than any other, and always with the sole object of grasping it as a whole and obtaining a clear knowledge and perception of its manifold changes of quality.
We may certainly assume that in the tones of the human larynx, as in all other reed instruments, the upper partial tones would decrease in force as they increase in pitch, if they could be observed without the resonance of the cavity of the mouth. In reality they satisfy this assumption tolerably well, for those vowels which are spoken with a wide funnel-shaped cavity of the mouth, as A [a in art], or Ä [a in bat lengthened, which is nearly the same as a in bare]. But this relation is materially altered by the resonance which takes place in the cavity of the mouth. The more this cavity is narrowed, either by the lips or the tongue, the more distinctly marked is its resonance for tones of determinate pitch, and the more therefore does this resonance reinforce those partials in the compound tone produced by the vocal chords, which approach the favoured pitch, and the more, on the contrary, will the others be damped. Hence on investigating the compound tones of the human voice by means of resonators, we find pretty uniformly that the first six to eight partials are clearly perceptible, but with very different degrees of force according to the different forms of the cavity of the mouth, sometimes screaming loudly into the ear, at others scarcely audible.
Under these circumstances the investigation of the resonance of the cavity of the mouth is of great importance. The easiest and surest method of finding the tones to which the air in the oral cavity is tuned for the different shapes it assumes in the production of vowels, is that which is used for glass bottles and other spaces filled with air. That is, tuning-forks of different pitches have to be struck and held before the opening of the air chamber — in the present case the open mouth — and the louder the proper tone of the fork is heard, the nearer does it correspond with one of the proper tones of the included mass of air.[70] Since the shape of the oral cavity can be altered at pleasure, it can always be made to suit the tone of any given tuning-fork, and we thus easily discover what shape the mouth must assume for its included mass of air to be tuned to a determinate pitch.
Having a series of tuning-forks at command, I was thus able to obtain the following results: —
The pitch of strongest resonance of the oral cavity depends solely upon the vowel for pronouncing which the mouth has been arranged, and alters considerably for even slight alterations in the vowel quality, such, for example, as occur in the different dialects of the same language. On the other hand, the proper tones of the cavity of the mouth are nearly independent of age and sex. I have in general found the same resonances in men, women, and children. The want of space in the oral cavity of women and children can be easily replaced by a great closure of its opening, which will make the resonance as deep as in the larger oral cavities of men.[71]
The vowels can be arranged in three series, according to the position of the parts of the mouth, which may be written thus, in accordance with Du Bois-Reymond the elder[72]: —
The vowel A [a in father, or Scotch a in man] forms the common origin of all three series. With this vowel corresponds a funnel-shaped resonance cavity, enlarging with tolerably uniformity from the larynx to the lips. For the vowels of the lower series, O [o in more] and U [oo in poor], the opening of the mouth is contracted by means of the lips, more for U than for O, while the cavity is enlarged as much as possible by depression of the tongue, so that on the whole it becomes like a bottle without a neck, with rather a narrow mouth, and a single unbroken cavity.[73] The pitch of such a bottle-shaped chamber is lower the larger its cavity and the narrower its mouth. Usually only one upper partial with strong resonance can be clearly recognised; when other proper tones exist they are comparatively very high, or have only weak resonance. In conformity with these results, obtained with glass bottles, we find that for a very deep hollow U [oo in poor nearly], where the oral cavity is widest and the mouth narrowest, the resonance is deepest and answers to the unaccented \(f\). On passing from U to O [o in more nearly] the resonance gradually rises; and for a full, ringing, pure O the pitch is \(b'\flat\). The position of the mouth for O is peculiarly favourable for resonance, the opening of the mouth being neither too large nor too small, and the internal cavity sufficiently spacious. Hence if a \(b'\flat\) tuning-fork be struck and held before the mouth while O is gently uttered, or the O-position merely assumed without really speaking, the tone of the fork will resound so fully and loudly that a large audience can hear it. The usual \(a'\) tuning-fork of musicians may also be used for this purpose, but then it will be necessary to make a somewhat duller O, if we wish to bring out the full resonance.
On gradually bringing the shape of the mouth from the position proper to O, through those due to O\(^a\) [nearly o in cot, with rather more of the O sound], and A\(^o\) [nearly \(au\) in \(caught\), with rather more of the A sound] into that for A [Scotch a in man, with rather more of an O quality in it than English a in father], the resonance gradually rises an Octave, and reaches \(b''\flat\). This tone corresponds with the North German A; the somewhat brighter A [a in father] of the English and Italians, rises up to \(d'''\), or a major Third higher. It is particularly remarkable what little differences in pitch correspond to very sensible varieties of vowel quality in the neighbourhood of A; and I should therefore recommend philologists who wish to define the vowels of different languages to fix them by the pitch of loudest resonance.[74]
For the vowels already mentioned I have not been able to detect any second proper tone, and the analogy of the phenomena presented by artificial resonance chambers of similar shapes would hardly lead us to expect any of sensible loudness. Experiments hereafter described shew that the resonance of this single tone is sufficient to characterise the vowels above mentioned.
The second series of vowels consists of A, Ä, E, I. The lips are drawn so far apart that they no longer contract the issuing stream of air, but a fresh constriction is formed between the front (middle) parts of the tongue and the hard palate, the space immediately above the larynx being widened by depressing the root of the tongue, and hence causing the larynx to rise simultaneously. The form of the oral cavity consequently resembles a bottle with a narrow neck. The belly of the bottle is behind, in the pharynx, and its neck is the narrow passage between the upper surface of the tongue and the hard palate. In the above series of letters, Ä, E, I, these changes increase until for I the internal cavity of the bottle is greatest and the neck narrowest. For Ä [the broadest French ê, broader than e in there, and nearly as broad as a in bat lengthened, with which the name of their city is pronounced by the natives of Bath], the whole channel is, however, tolerably wide, so that it is quite easy to see down to the larynx when the laryngoscope is used. Indeed this vowel gives the very best position of the mouth for the application of this instrument, because the root of the tongue, which impedes the view when A is uttered, is depressed, and the observer can see over and past it.
When a bottle with a long narrow neck is used as a resonance chamber, two simple tones are readily discovered, of which one can be regarded as the proper tone of the belly, and the other as that of the neck of the bottle. Of course the air in the belly cannot vibrate quite independently of that in the neck, and both proper tones in question must consequently be different, and indeed somewhat deeper than they would be if belly and neck were separate and had their resonance examined independently. The neck is approximately a short pipe open at both ends. To be sure, its inner end debouches into the cavity of the bottle instead of the open air, but if the neck is very narrow, and the belly of the bottle very wide, the latter may be looked upon in some respects as an open space with regard to the vibrations of the air inclosed in the neck. These conditions are best satisfied for I, in which the length of the channel between tongue and palate, measured from the upper teeth to the back edge of the bony palate, is about 6 centimetres [2.36 inches]. An open pipe of this length when blown would give \(e''''\), while the observations made for determining the tone of loudest resonance for I gives nearly \(d''''\), which is as close an agreement as could possibly have been expected in such an irregularly shaped pipe as that formed by the tongue and palate.
In accordance with these experiments the vowels Ä, E, I, have each a higher and a deeper resonance tone. The higher tones continue the ascending series of the proper tones of the vowels U, O, A. By means of tuning-forks I found for Ä a tone between \(g'''\) and \(a'''\flat\), and for E the tone \(b'''\flat\). I had no fork suitable for I, but by means of the whistling noise of the air, to be considered presently (p. 108b), its proper tone was determined with tolerable exactness to be \(d''''\). The deeper proper tones which are due to the back part of the oral cavity are rather more difficult to discover. Tuning-forks may be used, but the resonance is comparatively weak, because it must be conducted through the long narrow neck of the air chamber. It must further be remembered that this resonance only occurs during the time that the corresponding vowel is gently whispered, and disappears as soon as the whisper ceases, because the form of the chamber on which the resonance depends then immediately changes. The tuning-forks after being struck must be brought as close as possible to the opening of the air chamber which lies behind the upper teeth. By this means I found \(d''\) for Ä and \(f'\) for E. For I, direct observation with tuning-forks was not possible; but from the upper partial tones, I conclude that its proper tone is as deep as that of U, or near \(f\). Hence, when we pass from A to I, these deeper proper tones of the oral cavity sink, and the higher ones rise in pitch.[75]
For the third series of vowels from A through Ö [French eu in peu, or the deeper eu in peuple], towards Ü [French u in pu, which is rather deeper than the German sound], we have the same internal positions of the mouth as in the last-named series of vowels. For Ü the mouth is placed in nearly the same position as for a vowel lying between E and I, and for Ö as for an E which inclines towards Ä. In addition to the constriction between the tongue and palate as in the second series, we have also a constriction of the lips, which are made into a sort of tube, forming a front prolongation of that made by the tongue and palate. The air chamber of the mouth, therefore, in this case also resembles a bottle with a neck, but the neck is longer than for the second series of vowels. For I the neck was 6 centimetres (2.36 inches) long, for Ü, measured from the front edge of the upper teeth to the commencement of the soft palate, it is 8 centimetres (3.15 inches). The pitch of the higher proper tone corresponding to the resonance of the neck must be, therefore, about a Fourth deeper than for I. If both ends were free, a pipe of this length would give \(b'''\), according to the usual calculation. In reality it resounded for a fork lying between \(g'''\) and \(a'''\flat\) a divergence similar to that found for I, and also probably attributable to the back end of the tube debouching into a wider but not quite open space. The resonance of the back space has to be observed in the same way as for the I series. For Ö it is \(f'\) the same as for E, and for Ü it is \(f\), the same as for I.
The fact that the cavity of the mouth for different vowels is tuned to different pitches was first discovered by Donders,[76] not with the help of tuning-forks, but by the whistling noise produced in the mouth by whispering. The cavity of the mouth thus reinforces by its resonance the corresponding tones of the windrush, which are produced partly in the contracted glottis, [77] and partly in the forward contracted passages of the mouth. In this way it is not usual to obtain a complete musical tone; this only happens, without sensible change of the vowel, for Ü and U, when a real whistle is produced. This, however, would be a fault in speaking. We have rather only such a degree of reinforcement of the noise of the air as occurs in an organ pipe, which does not speak well, either from a badly-constructed lip or an insufficient pressure of wind. A noise of this kind, although not brought up to being a complete musical tone, has nevertheless a tolerably determinate pitch, which can be estimated by a practised ear. But, as in all cases where tones of very different qualities have to be compared, it is easy to make a mistake in the Octave. However, after some of the important pitches have been determined by tuning-forks, and others, as Ü and Ö, by allowing the whisper to pass into a regular whistle, the rest are easily determined by arranging them in a melodic progression with the first. Thus the series: —
| Clear A | Ä | E | I |
| [a in father] |
[a in mat] |
[e in there] |
[i in machine] |
forms an ascending minor chord of \(g\) in the second Inversion \(6 \atop 4\), [with the Fifth in the bass,] and can be readily compared with the same melodic progression on the pianoforte. I was able to determine the pitch for clear A, Ä, and E by tuningforks, and hence to fix that for I also.[78]
For U it is also by no means easy to find the pitch of the resonance by a fork, as the smallness of the opening makes the resonance weak. Another phenomenon has guided me in this case. If I sing the scale from \(c\) upwards, uttering the vowel U for each note, and taking care to keep the quality of the vowel correct, and not allowing it to pass into O,[79] I feel the agitation of the air in the mouth, and even on the drums of both ears, where it excites a tickling sensation, most powerfully when the voice reaches \(f\). As soon as \(f\) is passed the quality changes, the strong agitation of the air in the mouth and the tickling in the ears cease. For the note \(f\) the phenomenon in this case is the same as if a spherical resonance chamber were placed before a tongue of nearly the same pitch as its proper tone. In this case also we have a powerful agitation of the air within the sphere and a sudden alteration of quality of tone, on passing from a deeper pitch of the mass of air through that of the tongue to a higher. The resonance of the mouth for U is thus fixed at \(f\) with more certainty than by means of tuning-forks. But we often meet with a U of higher resonance, more resembling O, which I will represent by the French Ou. Its proper tone may rise as high as \(f'\).[80] The resonance of the cavity of the mouth for different vowels may then be expressed in the notes as follows:
The mode in which the resonance of the cavity of the mouth acts upon the quality of the voice, is then precisely the same as that which we discovered to exist for artificially constructed reed pipes. All those partial tones are reinforced which coincide with a proper tone of the cavity of the mouth, or have a pitch sufficiently near to that of such a tone, while the other partial tones will be more or less damped. The damping of those partial tones which are not strengthened is the more striking the narrower the opening of the mouth, either between the lips as for U, or between the tongue and palate as for I and Ü.
These differences in the partial tones of the different vowel sounds can be easily and clearly recognised by means of resonators, at least within the once and twice accented Octaves [264 to 1056 vib.]. For example, apply a \(b'\flat\) resonator to the ear, and get a bass voice, that can preserve pitch well and form its vowels with purity, to sing the series of vowels to one of the harmonic under tones of \(b'\flat\), such as \(b\flat, \; e\flat, \; B\flat, \; G\flat, \; E\flat\). It will be found that for a pure, full-toned O the \(b'\flat\) of the resonator will bray violently into the ear. The same upper partial tone is still very powerful for a clear Ä and a tone intermediate between A and Ö, but is weaker for A, E, Ö, and weakest of all for U and I. It will also be found that the resonance of O is materially weakened if it is taken too dull, approaching U, or too open, becoming A°. But if the \(b''\flat\) resonator be used, which is an Octave higher, it is the vowel A that excites the strongest sympathetic resonance; while O, which was so powerful with the \(b'\flat\) resonator, now produces only a slight effect.
For the high upper partials of Ä, E, I, no resonators can be made which are capable of sensibly reinforcing them. We are, then, driven principally to observations made with the unassisted ear. It has cost me much trouble to determine these strengthened partial tones in the vowels, and I was not acquainted with them when my previous accounts were published.[81] They are best observed in high notes of women’s voices, or the falsetto of men’s voices. The upper partials of high notes in that part of the scale are not so nearly of the same pitch as those of deeper notes, and hence they are more readily distinguished. On \(b'\flat\), for example, women’s voices could easily bring out all the vowels, with a full quality of tone, but at higher pitches the choice is more limited. When \(b'\flat\) is sung, then, the Twelfth \(f''\) is heard for the broad Ä, the double Octave \(b'''\flat\) for E, the high Third \(d''''\) for I, all clearly, the last even piercingly. [See table on p. 124, note.] [82]
Further, I should observe, that the table of notes given on the preceding page, relates only to those kinds of vowels which appear to me to have the most characteristic quality of tone, but that in addition to these, all intermediate stages are possible, passing insensibly from one to the other, and are actually used partly in dialects, partly by particular individuals, partly in peculiar pitches while singing, or to give a more decided character while whispering.
It is easy to recognise, and indeed is sufficiently well known, that the vowels with a single resonance from U through O to clear A can be altered in continuous succession. But I wish further to remark, since doubts have been thrown on the deep resonance I have assigned to U, that when I apply to my ear a resonator tuned to \(f'\), and, singing upon \(f\) or \(B\flat\) as the fundamental tone, try to find the vowel resembling U which has the strongest resonance, it does not answer to a dull U, but to a U on the way to O.[83]
Then again transitions are possible between the vowels of the A — O — U series and those of the A — Ö — Ü series, as well as between the last named and those of the A — E — I series. I can begin on the position for U, and gradually transform the cavity of the mouth, already narrowed, into the tube-like forms for Ö and Ü, in which case the high resonance becomes more distinct and at the same time higher, the narrower the tube is made. If we make this transition while applying a resonator between \(b'\flat\) and \(b''\flat\) to the ear, we hear the loudness of the tone increase at a certain stage of the transition, and then diminish again. The higher the resonator, the nearer must the vowel approach to Ö or Ü. With a proper position of the mouth the reinforced tone may be brought up to a whistle. Also in a gentle whisper, where the rustle of the air in the larynx is kept very weak, so that with vowels having a narrow opening of the mouth it can be scarcely heard, a strong fricative noise in the opening of the mouth is often required to make the vowel audible. That is to say, we then make the vowels more like their related consonants, English W and German J [English Y].
Generally speaking the vowels[84] with double resonance admit of numerous modifications, because any high pitch of one of the resonances may combine with any low pitch of the other. This is best studied by applying a resonator to the ear and trying to find the corresponding vowel degrees in the three series which reinforce its tone, and then endeavouring to pass from one of these to the other in such a way that the resonator should have a reinforced tone throughout.
Thus the resonator \(b'\flat\) answers to O, to an Äö and to an E which resembles Ä, and these sounds may pass continuously one into the other.
The resonator \(f'\) answers to the transition Ou — Ö — E. The resonator \(d''\) to Oa — Äö — Ä. In a similar manner each of the higher tones may be connected with various deeper tones. Thus assuming a position of the mouth which would give \(e'''\) for whistling, we can, without changing the pitch of the fricative sound in the mouth, whisper a vowel inclining to Ö or inclining to Ü, by allowing the fricative sound in the larynx to have a higher or deeper resonance in the back part of the mouth.[85]
In comparing the strength of the upper partials of different vowels by means of resonators, it is further to be remembered, that the reinforcement by means of the resonance of the mouth affects the prime tone of the note produced by the voice, as well as the upper partials. And as it is especially the vibrations of the prime, which by their reaction on the vocal chords retain these in regular vibratory motion, the voice speaks much more powerfully, when the prime itself receives such a reinforcement. This is especially observable in those parts of the scale which the singer reaches with difficulty. It may also be noted with reed pipes having metal tongues. When a resonance pipe is applied to them tuned to the tone of the tongue, or a little higher, extraordinarily powerful and rich tones are produced, by means of strong pressure but little wind, and the tongue oscillates in large excursions either way. The pitch of a metal tongue becomes a little flatter than before. This is not perceived with the human voice because the singer is able to regulate the tension of the vocal chords accordingly. Thus I find distinctly that at \(b'\flat\), the extremity of my falsetto voice, I can sing powerfully an O, an Ä, and an A on the way to Ö, which have their resonance at this pitch, whereas U, if it is not made to come very near O, and I, are dull and uncertain, with the expenditure of more air than in the former case. Regard must be had to this circumstance in experiments on the strength of upper partials, because those of a vowel which speaks powerfully, may become proportionally too powerful, as compared with those of a vowel which speaks weakly. Thus I have found that the high tones of the soprano voice which lie in the reinforcing region of the vowel A at the upper extremity of the doubly-accented [or one-foot] Octave, when sung to the vowel A, exhibit their higher Octave more strongly than is the case for the vowels E and I, which do not speak so well although the latter have their strong resonance at the upper end of the thrice-accented [or six-inch] Octave.
It has been already remarked (p. 39c) that the strength and amplitude of sympathetic vibration is affected by the mass and boundaries of the body which vibrates sympathetically. A body of considerable mass which can perform its vibrations as much as possible without any hindrance from neighbouring bodies, and has not its motion damped by the internal friction of its parts, after it has once been excited, can continue to vibrate for a long time, and consequently, if it has to be set in the highest degree of sympathetic vibration, the oscillations of the exciting tone must, for a comparatively long time, coincide with those proper vibrations excited in itself. That is to say, the highest degree of sympathetic resonance can be produced only by using tones which lie within very narrow limits of pitch. This is the case with tuning-forks and bells. The mass of air in the cavity of the mouth, on the other hand, has but slight density and mass, its walls, so far as they are composed of soft parts, are not capable of offering much resistance, are imperfectly elastic, and when put in vibration have much internal friction to stop their motion. Moreover the vibrating mass of air in the cavity of the mouth communicates through the orifice of the mouth with the outer air, to which it rapidly gives off large parts of the motion it has received. For this reason a vibratory motion once excited in the air filling the cavity of the mouth is very rapidly extinguished, as any one may easily observe by filliping his cheek with a finger when the mouth is put into different vowel positions. We thus very easily distinguish the pitch of the resonance for the various transitional degrees from O towards U in one direction and towards A in the other. But the tone dies away rapidly. The various resonances of the cavity of the mouth can also be made audible by rapping the teeth. Just for this reason a tone, which oscillates approximately in agreement with the few vibrations of such a brief resonance tone, will be reinforced by sympathetic vibration to an extent not much less than another tone which exactly coincides with the first; and the range of tones which can thus be sensibly reinforced by a given position of the mouth, is rather considerable.[86] This is confirmed by experiment. When I apply a \(b'\flat\) resonator to the right, and an \(f''\) resonator to the left ear and sing the vowel O on \(B\flat\), I find a reinforcement not only of the 4th partial \(b'\flat\) which answers to the proper tone of the cavity of the mouth, but also, very perceptibly, though considerably less, of \(f''\), the 6th partial, also. If I then change O into an A, until \(f''\) finds its strongest resonance, the reinforcement of \(b'\flat\) does not entirely disappear although it becomes much less.
The position of the mouth from O to \(_a\) appears to be that which is most favourable for the length of its proper tone and the production of a resonance limited to a very narrow range of pitch. At least, as I have before remarked, for this position the reinforcement of a suitable tuning-fork is most powerful, and tapping the cheek or the lips gives the most distinct tone. If then for O the reinforcement by resonance extends to the interval of a Fifth, the intervals will be still greater for the other vowels. With this agree experiments. Apply any resonator to the ear, take a suitable under tone, sing the different vowels to this under tone, and let one vowel melt into another. The greatest reinforcements by resonance take place on that vowel or those vowels, for which one of the characteristic tones in the diagram p. 100b coincides with the proper tone of the resonator. But more or less considerable reinforcement is also observed for such vowels as have their characteristic tones at moderate differences of pitch from the proper tone of the resonator, and the reinforcement will be less the greater these differences of pitch.
By this means it becomes possible in general to distinguish the vowels from each other even when the note to which they are sung is not precisely one of the harmonic under tones of the vowels. From the second partial tone onwards, the intervals are narrow enough for one or two of the partials to be distinctly reinforced by the resonance of the mouth. It is only when the proper tone of the cavity of the mouth falls midway between the prime tone of the note sung by the voice and its higher Octave, or is more than a Fifth deeper than that prime tone, that the characteristic resonance will be weak.
Now in speaking, both sexes choose one of the deepest positions of their voice. Men generally choose the upper half of the great (or eight-foot) Octave; and women the upper half of the small (or four-foot) Octave,[87] With the exception of U, which admits of fluctuations in its proper tone of nearly an Octave, all these pitches of the speaking voice have the corresponding proper tones of the cavity of the mouth situated within sufficiently narrow intervals from the upper partials of the speaking tone to create sensible resonance of one or more of these partials, and thus characterise the vowel.[88] To this must be added that the speaking voice, probably through great pressure of the vocal ligaments upon one another, converting them into striking reeds, has a jarring quality of tone, that is, possesses stronger upper partials than the singing voice.
In singing, on the other hand, especially at higher pitches, conditions are less favourable for the characterisation of vowels. Every one knows that it is generally much more difficult to understand words when sung than when spoken, and that the difficulty is less with male than with female voices, each having been equally well cultivated. Were it otherwise, 'books of the words' at operas and concerts would be unnecessary. Above \(f'\), the characterisation of U becomes imperfect even if it is closely assimilated to O. But so long as it remains the only vowel of indeterminate sound, and the remainder allow of sensible reinforcement of their upper partials in certain regions, this negative character will distinguish U. On the other hand a soprano voice in the neighbourhood of \(f''\) should not be able to clearly distinguish U, O, and A; and this agrees with my own experience. On singing the three vowels in immediate succession, the resonance \(f'''\) for A will, however, be still somewhat clearer in the cavity of the mouth when tuned for \(b''\flat\), than when it is tuned to \(b'\flat\) for O. The soprano voice will in this case be able to make the A clearer, by elevating the pitch of the cavity of the mouth towards \(d'''\) and thus making it approach to \(f'''\). The O, on the other hand, can be separated from U by approaching O\(_a\), and giving the prime more decisive force. Nevertheless these vowels, if not sung in immediate succession, will not be very clearly distinguished by a listener who is unacquainted with the mode of pronouncing the vowels that the soprano singer uses.[89]
A further means of helping to discriminate vowels, moreover, is found in commencing them powerfully. This depends upon a general relation in bodies excited to sympathetic vibration. Thus, if we excite sympathetic vibration in a suitable body with a tone somewhat different from its proper tone, by commencing it suddenly with great power, we hear at first, in addition to the exciting tone which is reinforced by resonance, the proper tone of the sympathetically vibrating body.[90] But the latter soon dies away, while the first remains. In the case of tuning-forks with large resonator, we can even hear beats between the two tones. Apply a \(b'\flat\) resonator to the ear, and commence singing the vowel O powerfully on \(g\), of which the upper partials \(g'\) and \(d''\) have only a weak lasting resonance in the cavity of the mouth, and you may hear immediately at the commencement of the vowel, a short sharp beat between the \(b'\flat\) of the cavity of the mouth and of the resonator. On selecting another vowel, this \(b'\flat\) vanishes, which shews that the pitch of the cavity of the mouth helps to generate it. In this case then also the sudden commencement of the tones \(g''\) and \(d''\) belonging to the compound tone of the voice, excites the intermediate proper tone \(b'\flat\) of the cavity of the mouth, which rapidly fades. The same thing may be observed for other pitches of the resonator used, when we sing notes, powerfully commenced, which have upper partials that are not reinforced by the resonator, provided that a vowel is chosen with a characteristic pitch which answers to the pitch of the resonator. Hence it results that when any vowel in any pitch is powerfully commenced, its characteristic tone becomes audible as a short beat. By this means the vowel may be distinctly characterised at the moment of commencement, even when it becomes intermediate on long continuance. But for this purpose, as already remarked, an exact and energetic commencement is necessary. How much such a commencement assists in rendering the words of a singer intelligible is well known. For this reason also the vocalisation of the briefly-uttered words of a reciting parlando, is more distinct than that of sustained song.[91]
Moreover vowels admit of other kinds of alterations in their qualities of tone, conditioned by alterations of their characteristic tones within certain limits. Thus the resonating capability of the cavity of the mouth may undergo in general alterations in strength and definition, which would render the character of the various vowels and their difference from one another in general more or less conspicuous or obscure. Flaccid soft walls in any passage with sonorous masses of air, are generally prejudicial to the force of the vibrations. Partly too much of the motion is given off to the outside through the soft masses, partly too much is destroyed by friction within them. Wooden organ pipes have a less energetic quality of tone than metal ones, and those of pasteboard a still duller quality, even when the mouthpiece remains unaltered. The walls of the human throat, and the cheeks, are, however, much more yielding than pasteboard. Hence if the tone of the voice with all its partials is to meet with a powerful resonance and come out unweakened, these most flaccid parts of the passage for our voice, must be as much as possible thrown out of action, or else rendered elastic by tension, and in addition the passage must be made as short and wide as possible. The last is effected by raising the larynx. The soft wall of the cheeks can be almost entirely avoided, by taking care that the rows of teeth are not too far apart. The lips, when their co-operation is not necessary, as it is for Ö and Ü, may be held so far apart that the sharp firm edges of the teeth define the orifice of the mouth. For A the angles of the mouth can be drawn entirely aside. For O they can be firmly stretched by the muscles above and below them (levator anguli oris and triangularis menti), which then feel like stretched cords to the touch, and can be thus pressed against the teeth, so that this part of the margin of the orifice of the mouth is also made sharp and capable of resisting.
In the attempt to produce a clear energetic tone of the voice we also become aware of the tension of a large number of muscles lying in front of the throat, both those which lie between the under jaw and the tongue-bone and help to form the floor of the cavity of the mouth (mylohyoideus, geniohyoideus, and perhaps also biventer), and likewise those which run down near the larynx and air tubes, and draw down the tongue-bone (sternohyoideus, sternothyroideus and thyrohyoideus). Without the counteraction of the latter, indeed, considerable tension of the former would be impossible. Besides this a contraction of the skin on both sides of the larynx which takes place at the commencement of the tone of the voice, shews that the omohyoideus muscle, which runs obliquely down from the tongue-bone backwards to the shoulder-blade, is also stretched. Without its co-operation the muscles arising from the under jaw and breast-bone would draw the larynx too far forwards. Now the greater part of these muscles do not go to the larynx at all, but only to the tongue-bone, from which the larynx is suspended. Hence they cannot directly assist in the formation of the voice, so far as this depends upon the action of the larynx. The action of these muscles, so far as I have been able to observe it on myself, is also much less when I utter a dull guttural A, than when I endeavour to change it into a ringing, keen and powerfully penetrating A. Ringing and keen, applied to a quality of tone, imply many and powerful upper partials, and the stronger they are, of course the more marked are the differences of the vowels which their own differences condition. A singer, or a declaimer, will occasionally interpose among his bright and rich tones others of a duller character as a contrast. Sharp characterisation of vowel quality is suitable for energetic, joyful or vigorous frames of mind; indifferent and obscure quality of tone for sad and troubled, or taciturn states. In the latter case speakers like to change the proper tone of the vowels, by drawing the extremes closer to a middle Äö (say the short German E [the final English obscure A in idea]), and hence select somewhat deeper tones in place of the high tones of A, E, I.
A peculiar circumstance must also be mentioned which distinguishes the human voice from all other instruments and has a peculiar relation to the human ear. Above the higher reinforced partial tones of I, in the neighbourhood of \(e''''\) up to \(g''''\) [2640 to 3168 vib.] the notes of a pianoforte have a peculiar cutting effect, and we might be easily led to believe that the hammers were too hard, or that their mechanism somewhat differed from that of the adjacent notes. But the phenomenon is the same on all pianofortes, and if a very small glass tube or sphere is applied to the ear, the cutting effect ceases, and these notes become as soft and weak as the rest, but another and deeper series of notes now becomes stronger and more cutting. Hence it follows that the human ear by its own resonance favours the tones between \(e''''\) and \(g''''\), or, in other words, that it is tuned to one of these pitches.[92] These notes produce a feeling of pain in sensitive ears. Hence the upper partial tones which have nearly this pitch, if any such exist, are extremely prominent and affect the ear powerfully. This is generally the case for the human voice when it is strained, and will help to give it a screaming effect. In powerful male voices singing forte, these partial tones sound like a clear tinkling of little bells, accompanying the voice, and are most audible in choruses, when the singers shout a little. Every individual male voice at such pitches produces dissonant upper partials. When basses sing their high \(e'\), the 7th partial tone[93] is \(d''''\), the 8th \(e''''\), the 9th \(f''''\sharp\), and the 10th \(g''''\sharp\) Now, if \(e''''\) and \(f''''\sharp\) are loud, and \(d''''\) and \(g''''\sharp\), though weaker, are audible, there is of course a sharp dissonance. If many voices are sounding together, producing these upper partials with small differences of pitch, the result is a very peculiar kind of tinkling, which is readily recognised a second time when attention has been once drawn to it. I have not noticed any difference of effect for different vowels in this case, but the tinkling ceases as soon as the voices are taken piano; although the tone produced by a chorus will of course still have considerable power. This kind of tinkling is peculiar to human voices; orchestral instruments do not produce it in the same way either so sensibly or so powerfully. I have never heard it from any other musical instrument so clearly as from human voices.
The same upper partials are heard also in soprano voices when they sing forte; in harsh, uncertain voices they are tremulous, and hence shew some resemblance to the tinkling heard in the notes of male voices. But I have heard them brought out with exact purity, and continue to sound on perfectly and quietly, in some steady and harmonious female voices, and also in some excellent tenor voices. In the melodic progression of a voice part, I then hear these high upper partials of the four-times accented Octave, falling and rising at different times within the compass of a minor Third, according as different upper partials of the notes sung enter the region for which our ear is so sensitive. It is certainly remarkable that it should be precisely the human voice which is so rich in those upper partials for which the human ear is so sensitive. Madame E. Seiler, however, remarks that dogs are also very sensitive for the high \(e''''\) of the violin.
This reinforcement of the upper partial tones belonging to the middle of the four-times accented Octave, has, however, nothing to do with the characterisation of vowels. I have mentioned it here, merely because these high tones are readily remarked in investigations into the vowel qualities of tone, and the observer must not be misled to consider them as peculiar characteristics of individual vowels. They are simply a characteristic of strained voices.
The humming tone heard when singing with closed mouth, lies nearest to U. This hum is used in uttering the consonants, M, N and N\(^g\). The size of the exit of the air (the nostrils) is in this case much smaller in comparison with the resonant chamber (the internal nasal cavity) than the opening of the lips for U in comparison with the corresponding resonant chamber in the mouth. Hence, in humming, the peculiarities of the U tone are much enhanced. Thus although upper partials are present, even up to a considerably high pitch, yet they decrease in strength as they rise in pitch much faster than for U. The upper Octave is tolerably strong in humming, but all the higher partial tones are weak. Humming in the N-position differs a little from that in the M-position, by having its upper partials less damped than for M. But it is only at the instant when the cavity of the mouth is opened or closed that a clear difference exists between these consonants. We cannot enter into the details of the composition of the sound of the other consonants, because they produce noises which have no constant pitch, and are not musical tones, to which we have here to confine our attention.
The theory of vowel sounds here explained may be confirmed by experiments with artificial reed pipes, to which proper resonant chambers are attached. This was first done by Willis, who attached reed pipes to cylindrical chambers of variable length, and produced different tones by increasing the length of the resonant tube. The shortest tubes gave him I, and then E, A, O, up to U, until the tube exceeded the length of a quarter of a wave. On further increasing the length the vowels returned in converse order. His determination of the pitch of the resonant pipes agrees well with mine for the deeper vowels. The pitch found by Willis for the higher vowels was relatively too high, because in this case the length of the wave was smaller than the diameter of the tubes, and consequently the usual calculation of pitch from the length of the tubes alone was no longer applicable. The vowels E and I were also far from accurately resembling those of the voice, because the second resonance was absent, and hence, as Willis himself states, they could not be well distinguished.[94]
| Vowel | In the Word | Pitch, Willis | Pitch, Helmholtz | Length of Tube in Inches |
| O | No |
|
|
4.7 |
| A\(^o\) | Nought Paw |
|
|
3.8 3.05 |
| A | Part Pad |
|
|
2.2 1.8 |
| E | Pay Pet |
|
|
1.0 0.6 |
| I | See |
|
|
0.38 (?) |
The vowels are obtained much more clearly and distinctly with properly tuned resonators, than with cylindrical resonance chambers. On applying to a reed pipe which gave \(b\flat\), a glass resonator tuned to \(b\flat\), I obtained the vowel U; changing the resonator to one tuned for \(b'\flat\), I obtained O; the \(b''\flat\) resonator gave a rather close A, and the \(d'''\) resonator a clear A. Hence by tuning the applied chambers in the same way we obtain the same vowels quite independently of the form of the chamber and nature of its walls. I also succeeded in producing various grades of Ä, Ö, E, and I with the same reed pipe, by applying glass spheres into whose external opening glass tubes were inserted from 6 to 10 centimetres (2.36 to 3.94 inches) in length in order to imitate the double resonance of the oral cavity for these vowels.
Willis has also given another interesting method for producing vowels. If a toothed wheel, with many teeth, revolve rapidly, and a spring be applied to its teeth, the spring will be raised by each tooth as it passes, and a tone will be produced having its pitch number equal to the number of teeth by which it has been struck in a second. Now if one end of the spring is well fastened, and the spring be set in vibration, it will itself produce a tone which will increase in pitch as the spring diminishes in length. If then we turn the wheel with a constant velocity, and allow a watch spring of variable length to strike against its teeth, we shall obtain for a long spring a quality of tone resembling U, and as we shorten the spring other qualities in succession like O, A, E, I, the tone of the spring here playing the part of the reinforced tone which determines the vowel. But this imitation of the vowels is certainly much less complete than that obtained by reed pipes. The reason of this process also evidently depends upon our producing compound tones in which certain upper partials (which in this case correspond with the proper tones of the spring itself) are more reinforced than others.
Willis himself advanced a theory concerning the nature of vowel tones which differs from that I have laid down in agreement with the whole connection of all other acoustical phenomena. Willis imagines that the pulses of air which produce the vowel qualities, are themselves tones which rapidly die away, corresponding to the proper tone of the spring in his last experiment, or the short echo produced by a pulse or a little explosion of air in the mouth, or in the resonance chamber of a reed pipe. In fact something like the sound of a vowel will be heard if we only tap against the teeth with a little rod, and set the cavity of the mouth in the position required by the different vowels. Willis’s description of the motion of sound for vowels is certainly not a great way from the truth; but it only assigns the mode in which the motion of the air ensues, and not the corresponding reaction which this produces in the ear. That this kind of motion as well as all others is actually resolved by the ear into a series of partial tones, according to the laws of sympathetic resonance, is shewn by the agreement of the analysis of vowel qualities of tone made by the unarmed ear and by the resonators. This will appear still more clearly in the next chapter, where experiments will be described shewing the direct composition of vowel qualities from their partial tones.
Vowel qualities of tone consequently are essentially distinguished from the tones of most other musical instruments by the fact that the loudness of their partial tones does not depend solely upon their numerical order but preponderantly upon the absolute pitch of those partials. Thus when I sing the vowel A to the note \(E\flat\)[95], the reinforced tone \(b''\flat\) is the 12th partial of the compound tone; and when I sing the same vowel A to the note \(b'\flat\), the reinforced tone is still \(b''\flat\), but is now the 2nd partial of the compound tone sung.[96]
From the examples adduced to shew the dependence of quality of tone from the mode in which a musical tone is compounded, we may deduce the following general rules : —
1. Simple Tones, like those of tuning-forks applied to resonance chambers and wide stopped organ pipes, have a very soft, pleasant sound, free from all roughness, but wanting in power, and dull at low pitches.
2. Musical Tones, which are accompanied by a moderately loud series of the lower partial tones, up to about the sixth partial, are more harmonious and musical. Compared with simple tones they are rich and splendid, while they are at the same time perfectly sweet and soft if the higher upper partials are absent. To these belong the musical tones produced by the pianoforte, open organ pipes, the softer piano tones of the human voice and of the French horn. The last-named tones form the transition to musical tones with high upper partials ; while the tones of flutes, and of pipes on the flue-stops of organs with a low pressure of wind, approach to simple tones.
3. If only the unevenly numbered partials are present (as in narrow stopped organ pipes, pianoforte strings struck in their middle points, and clarinets), the quality of tone is hollow, and, when a large number of such upper partials are present, nasal. When the prime tone predominates the quality of tone is rich; but when the prime tone is not sufficiently superior in strength to the upper partials, the quality of tone is poor. Thus the quality of tone in the wider open organ pipes is richer than that in the narrower; strings struck with pianoforte hammers give tones of a richer quality than when struck by a stick or plucked by the finger; the tones of reed pipes with suitable resonance chambers have a richer quality than those without resonance chambers.
4. When partial tones higher than the sixth or seventh are very distinct, the quality of tone is cutting and rough. The reason for this will be seen hereafter to lie in the dissonances which they form with one another. The degree of harshness may be very different. When their force is inconsiderable the higher upper partials do not essentially detract from the musical applicability of the compound tones; on the contrary, they are useful in giving character and expression to the music. The most important musical tones of this description are those of bowed instruments and of most reed pipes, oboe (hautbois), bassoon (fagotto), harmonium, and the human voice. The rough, braying tones of brass instruments are extremely penetrating, and hence are better adapted to give the impression of great power than similar tones of a softer quality. They are consequently little suitable for artistic music when used alone, but produce great effect in an orchestra. Why high dissonant upper partials should make a musical tone more penetrating will appear hereafter.
As my friend, Mr. A. J. Hipkins, of Broadwoods', author of a paper on the 'History of the Pianoforte,' in the Journal of the Society of Arts (for March 9, 1883, with additions on Sept. 21, 1883), has paid great attention to the archaeology of the pianoforte, and from his position at Messrs. Broadwoods' has the best means at his disposal for making experiments, I requested him to favour me with his views upon the subject of the striking place and harmonics of pianoforte strings, and he has obliged me with the following observations : — 'Harpsichords and spinets, which were set in vibration by quill or leather plectra, had no fixed point for plucking the strings. It was generally from about \(\tfrac12\) to \(\tfrac17\) of the vibrating length, and although it had been observed by Huyghens and the Antwerp harpsichord maker Jan Couchet, that a difference of quality of tone could be obtained by varying the plucking place on the same string, which led to the so-called lute stop of the 18th century, no attempt appears to have been made to gain a uniform striking place throughout the scale. Thus in the latest improved spinet, a Hitchcock, of early 18th century, in my possession, the striking place of the \(c\)’s varies from \(\tfrac12\) to \(\tfrac17\), and in the latest approved harpsichord, a Kirkman of 1773, also in my possession, the striking distances vary from \(\tfrac12\) to \(\tfrac{1}{10}\) and for the lute stop from \(\tfrac{1}{29}\) to of the string, the longest distances in the bass of course, but all without apparent rule or proportion. Nor was any attempt to gain a uniform striking place made in the first pianofortes. Stein of Augsburg (the favourite pianoforte-maker of Mozart, and of Beethoven in his virtuoso time) knew nothing of it, at least in his early instruments. The great length of the bass strings as carried out on the single bellybridge copied from the harpsichord made a reasonable striking place for that part of the scale impossible.
'John Broadwood, about the year 1788, was the first to try to equalise the scale in tension and striking place. Ho called in scientific aid, and assisted by Signor Cavallo and the then Dr. Gray of the British Museum, he produced a divided belly-bridge, which shortening the too great length of the bass strings, permitted the establishment of a striking place, which, in intention, should be proportionate to the length of the string throughout. He practically adopted a ninth of the vibrating length of the string for his striking place, allowing some latitude in the treble. This division of the belly-bridge became universally adopted, and with it an approximately rational striking place.
'Carl Kützing (Das Wissenschaftliche der Fortepiano-Baukunst, 1844, p. 41) was enabled to propound from experience, that \(\tfrac18\) of the length of the string was the most suitable distance in a pianoforte for obtaining the best quality of tone from the strings. The love of noise or effect has, however, inclined makers to shorten distances, particularly in the trebles. Kützing appears to have met with in some instances, and Helmholtz has adopted that very exceptional measure for his table on p. 79c. I cannot say I have ever met with a striking place of this long distance from the wrestplank-bridge. The present head of the firm of Broadwood (Mr. Henry Fowler Broadwood) has arrived at the same conclusions as Kützing with respect to the superiority of the \(\tfrac18\)th distance, and has introduced it in his pianofortes. At \(\tfrac19\)th the hammers have to be softer to get a like quality of tone; an equal system of tension being presupposed.
'According to Young’s law, which Helmholtz by experiment confirms, the impact of the hammer abolishes the node of the striking place, and with it the partial belonging to it throughout the string. I do not find, however, that the hammer striking at the \(\tfrac18\)th eliminates the 8th partial. It is as audible, when touchod as an harmonic, as the 9th and higher partials. It is easy, on a long string of say from 25 to 45 inches, to obtain the series of upper partials up to the fifteenth. On a string of 45 inches I have obtained as far as the 23rd harmonic, the diameter of the wire being 1-17 mm. or .07 inches, and the tension being 71 kilogrammes or 156-6 lbs. The partials diminish in intensity with the reduction of the vibrating length; the 2nd is stronger than the 3rd, and the 3rd than the 4th, &c. Up to the 7th a good harmonic note can always be brought out. After the 8th, as Helmholtz says, the higher partials are all comparatively weak and become gradually fainter. To strengthen them we may use a narrower, harder hammer. To hear them with an ordinary hammer it is necessary to excite them by a firm blow of the hand upon the finger-key and to continue to hold it down. They sing out quite clearly and last a very sensible time. On removing the stop immediately after production, they last much longer and are much brighter.
'I do not think the treble strings are from shortness and stiffness incapable of forming high proper tones. If it were so the notes would be of a very different quality of tone to that which they are found to have. Owing to the very acute pitch of these tones our ears cannot follow them, but their existence is proved by the fact that instrument-makers often bring their treble striking place very near the wrestplauk-bridge in order to secure a brilliant tone effect, or ring, by the preponderance of these harmonics.
'The clavichord differs entirely from hammer and plectrum keyboard instruments in the note being started from the end, the tangent (brass pin) which stops the string being also the means of exciting the sound. But the thin brass wires readily break up into segments of short recurrence, the bass wires, which are most indistinct, being helped in the latest instruments by lighter octave strings, which serve to make the fundamental tones apparent.' See also the last note, p. 76d’, and App. XX. sect. N.— Translator.]
↵This rule is always sufficiently accurate for cutting organ pipes to their approximate length, and piercing them to bring out the Octave harmonic, and has long been used for these purposes in M. Cavaillé-Coll’s factory. The rule is not so safe for the square wooden as for the cylindrical metal pipes. The pitch of a pipe of known dimensions ought to be first ascertained by other means. Then this pitch number multiplied by the divisors in (3) and (4) should be used in place of the 20,080 or 510,000 of the rule, for all similar pipes.
As to strength of wind, as pressure varies from 2f to 3} inches, the pitch number increases by about 1 in 300, but as pressure varies from 3J to 4 inches, the pitch number increases by about 1 in 440, the whole increase of pressure from 2j to 4 inches increases the pitch number by 1 in 180.
For temperature, I found by numerous observations at very different temperatures that the following practical rule is sufficient for reducing the pitch number observed at one temperature to that due to another. It is not quite accurate, for the air blown from the bellows is often lower than the external temperature. Let \(P\) be the pitch number observed at a given temperature, and \(d\) the difference of temperature in degrees Fahr. Then the pitch number is \(P \times (1 \pm .00104 d)\) according as the temperature is higher or lower. The practical operation is as follows: supposing \(P = 528\), and \(d = 14\) increase of temperature. To 528 add 4 in 100, or 21.12, giving 549.12. Divide by 1000' to 2 places of decimals, giving .55. Multiply by d = 14, giving 7.70. Adding this to 528, we get 535.7 for the pitch number at the new temperature. — Translator.] ↵
| for diameter | .45 | .75 | 1.25 | 2.08 | 3.47 English inches |
| pitch various, velocity | 1064.26 | 1072.53 | 1078.71 | 1081.78 | 1083.13 English feet |
| pitch 260 vib., velocity | 1062.12 | 1072.47 | 1078.73 | 1082.51 | 1084.88 English feet |
Fig. 28, p. 95b, shown the vibrator of an harmonium, not of an organ pipe. The figures are the same as in all the German editions. — Translator.]↵
| Pitch | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8,&c. |
|
|
\(f\) | \(f\) | \(p\) | \(mf\) | \(p\) | ... | ... | |
|
|
\(f\) | \(f\) | \(p\) | \(mf\) | ... | \(mf\) | \(pp\) | |
|
|
\(f\) | \(f\) | \(p\) | \(mf\) | ... | \(mf\) | \(pp\) | |
|
|
\(f\) | Just Discernible | \(f\) | ... | \(mf\) | \(mf\) | \(p\) | \(pp\) |
|
|
\(f\) | \(f\) | ... | \(mf\) | \(p\) | \(mf\) | \(pp\) | |
|
|
\(f\) | \(mf\) | ... | \(p\) | \(p\) | \(mf\) | \(pp\) | |
|
|
\(f\) | \(mf\) | \(p\) | \(mf\) | \(p\) | \(p\) | \(pp\) |
| Notes | \(e'\flat\) | \(f'\) | \(g'\) | \(a'\flat\) | \(b'\flat\) | \(c''\) | \(d''\flat\) | \(d''\) | \(e''\flat\) |
|---|---|---|---|---|---|---|---|---|---|
| Just cents | 0, | 204, | 386, | 498, | 702, | 884, | 996, | 1088, | 1200 |
| Harmonic cents | 0, | 204, | 386, | 551, | 702, | 841, | 969, | 1088, | 1200 |
| Harmonics, No. | 8, | 9, | 10, | 11, | 12, | 13, | 14, | 15, | 16. |
The mechanism is as follows (pp. 163-171): —
1. Lower thick. The hindmost points of the pyramids (arytenoid cartilages) close together, an elliptical slit between the vocal ligaments (or chords), which vibrate through their whole length, breadth, and thickness fully, loosely, and visibly. The lid (epiglottis) is low.
2. Upper thick. The elliptical chink disappears and becomes linear. The lid (epiglottis) rises ; the vocal ligaments are stretched.
3. Lower thin. The lid (epiglottis) is more raised, so as to shew the cushion below it, the whole larynx and the insertions of the vocal ligaments in the shield (thyroid) cartilage. The vocal ligaments are quite still, and their vibrations are confined to the thin inner edges. The vocal ligaments are made thinner and transparent, as shewn by illumination from below. Male voices cease here.
4. Upper thin. An elliptical slit again forms between the vocal ligaments. When this is used by men it gives the falsetto arising from the upper thin being carried below its true place. This slit is gradually reduced in size as the contralto and soprano voices ascend.
5. Small. The back part of the glottis contracts for at least two-thirds of its length, the vocal ligaments being pressed together so tightly that scarcely any trace of a slit remains, and no vibrations are visible. The front part opens as an oval chink, and the edges of this vibrate so markedly that the outline is blurred. The drawings of the two lost registers (pp. 168-169) were made from laryngoscopic examination of a lady.
Reference should be made to the book itself for full explanations, and the reader should especially consult Mr. Behnke’s admirable little work The Mechanism of the Human Voice (Curwen, 3rd ed., 1881, pp. 125). — Translator.]
↵| Vowel | Pitch according to Donders | Pitch according to Helmholtz |
| \(\text{U}\) \(\text{O}\) \(\text{A}\) \(\text{Ö}\) \(\text{Ü}\) \(\text{E}\) \(\text{I}\) |
|
|
[The extreme divergence of results obtained by different investigators shews the inherent difficulties of the determination, which (as already indicated) arise partly from different values attributed to the vowels, partly from the difficulty of retaining the form of the mouth steadily for a sufficient time, partly from the wide range of tones which the same cavity of the mouth will more or loss reinforce, partly from the difficulty of judging of absolute pitch in general, and especially of the absolute pitch of a scarcely musical whisper, and other causes. In C. L. Merkel's Physiologic der menschlichen Sprache (Leipzig, 1866), p. 47, a table is given of the results of Reyher, Hellwag, Flörcke, and Donders (the latter differing materially from that just given by Prof. Helmholtz), and on Merkel's p. 109, he adds his last results. These are reproduced in the following table with the notes, and their pitch to the nearest vibration, taking \(a' \; 440\), and supposing equal temperament. To these I add the results of Donders, as just given, and of Helmholtz, both with pitches similarly assumed. Koenig (Comptes Rendus, April 25, 1870) also gives his pitches with exact numbers, reckoned as Octaves of the 7th harmonic of \(c' \; 256\), and hence called \(b\flat\), although they are nearer the \(a\) of this standard. Reference should also be made to Dr. Koenig's paper on 'Manometric Flames' translated in the Philosophical Magazine, 1873, vol. xlv. pp. 1-18, 105-114. Lastly, Dr. Moritz Trautmann (Anglia, vol. i. p. 590) very confidently gives results utterly different from all the above, which I subjoin with the pitch as before. I give the general form of the vowel at the head of each column, and when the writer distinguishes different forms I add them immediately before the resonance note. Thus we have Helmholtz's Ou between U and O; Merkel’s O\(^a\) between O and A, his obscure A`, E` and clear A', E'; Trautmann’s O` = Italian open O, and (as he says) English a in all (which is, however, slightly different), O' ordinary o in Berliner ohne, E' Berlin Schnee, E` French père (the same as Ä?), Ö' Berlin schön, French peu, Ö` French leur. Of course this is far from exhausting the list of vowels in actual use.
| Observer | U | O | A | Ä | E | I | Ü | Ö |
| 1. Reyher |
|
|
|
|
|
|
||
| 2. Hellwag |
|
|
|
|
|
|
|
|
| 3. Flörcke |
|
|
|
|
|
|
|
|
| 4. Donders according to Helmholtz |
|
|
|
|
|
|
|
|
| 5. Donders according to Merkel |
|
|
|
|
|
|
|
|
| 6. Helmholtz | U, Ou. |
|
|
|
|
|
|
|
| 7. Merkel |
|
O |
A`, A', |
or |
E`, E', |
|
|
or |
| 8. Koenig, 7th harmonics |
|
|
|
|
|
|||
| 9. Trautmann |
|
O`, O', |
|
=E`? | E`, E', |
|
|
Ö`, Ö', \(a''' \; 1760 \) |