At the end of the last chapter we came upon the remarkable fact that the human ear is capable, under certain conditions, of separating the musical tone produced by a single musical instrument, into a series of simple tones, namely, the prime partial tone, and the various upper partial tones, each of which produces its own separate sensation. That the ear is capable of distinguishing from each other tones proceeding from different sources, that is, which do not arise from one and the same sonorous body, we know from daily experience. There is no difficulty during a concert in following the melodic progression of each individual instrument or voice, if we direct our attention to it exclusively; and, after some practice, most persons can succeed in following the simultaneous progression of several united parts. This is true, indeed, not merely for musical tones, but also for noises, and for mixtures of music and noise. When several persons are speaking at once, we can generally listen at pleasure to the words of any single one of them, and even understand those words, provided that they are not too much overpowered by the mere loudness of the others. Hence it follows, first, that many different trains of waves of sound can be propagated at the same time through the same mass of air, without mutual disturbance; and, secondly, that the human ear is capable of again analysing into its constituent elements that composite motion of the air which is produced by the simultaneous action of several musical instruments. We will first investigate the nature of the motion of the air when it is produced by several simultaneous musical tones, and how such a compound motion is distinguished from that due to a single musical tone. We shall see that the ear has no decisive test by which it can in all cases distinguish between the effect of a motion of the air caused by several different musical tones arising from different sources, and that caused by the musical tone of a single sounding body. Hence the ear has to analyse the composition of single musical tones, under proper conditions, by means of the same faculty which enabled it to analyse the composition of simultaneous musical tones. We shall thus obtain a clear conception of what is meant by analysing a single musical tone into a series of partial simple tones, and we shall perceive that this phenomenon depends upon one of the most essential and fundamental properties of the human ear.

We begin by examining the motion of the air which corresponds to several simple tones acting at the same time on the same mass of air. To illustrate this kind of motion it will be again convenient to refer to the waves formed on a calm surface of water. We have seen (p. 9) that if a point of the surface is agitated by a stone thrown upon it, the agitation is propagated in rings of waves over the surface to more and more distant points. Now, throw two stones at the same time on to different points of the surface, thus producing two centres of agitation. Each will give rise to a separate ring of waves, and the two rings gradually expanding, will finally meet. Where the waves thus come together, the water will be set in motion by both kinds of agitation at the same time, but this in no wise prevents both series of waves from advancing further over the surface, just as if each were alone present and the other had no existence at all. As they proceed, those parts of both rings which had just coincided, again appear separate and unaltered in form. These little waves, caused by throwing in stones, may be accompanied by other kinds of waves, such as those due to the wind or a passing steamboat. Our circles of waves will spread out over the water thus agitated, with the same quiet regularity as they did upon the calm surface. Neither will the greater waves be essentially disturbed by the less, nor the less by the greater, provided the waves never break; if that happened, their regular course would certainly be impeded.

Indeed it is seldom possible to survey a large surface of water from a high point of sight, without perceiving a great multitude of different systems of waves mutually overtopping and crossing each other. This is best seen on the surface of the sea, viewed from a lofty cliff, when there is a lull after a stiff breeze. We first see the great waves, advancing in far-stretching ranks from the blue distance, here and there more clearly marked out by their white foaming crests, and following one another at regular intervals towards the shore. From the shore they rebound, in different directions according to its sinuosities, and cut obliquely across the advancing waves. A passing steamboat forms its own wedge-shaped wake of waves, or a bird, darting on a fish, excites a small circular system. The eye of the spectator is easily able to pursue each one of these different trains of waves, great and small, wide and narrow, straight and curved, and observe how each passes over the surface, as undisturbedly as if the water over which it flits were not agitated at the same time by other motions and other forces. I must own that whenever I attentively observe this spectacle it awakens in me a peculiar kind of intellectual pleasure, because it bares to the bodily eye, what the mind's eye grasps only by the help of a long series of complicated conclusions for the waves of the invisible atmospheric ocean.

We have to imagine a perfectly similar spectacle proceeding in the interior of a ball-room, for instance. Here we have a number of musical instruments in action, speaking men and women, rustling garments, gliding feet, clinking glasses, and so on. All these causes give rise to systems of waves, which dart through the mass of air in the room, are reflected from its walls, return, strike the opposite wall, are again reflected, and so on till they die out. We have to imagine that from the mouths of men and from the deeper musical instruments there proceed waves of from 8 to 12 feet in length [\(c\) to \(F\)], from the lips of the women waves of 2 to 4 feet in length [\(c''\) to \(c'\)], from the rustling of the dresses a fine small crumple of wave, and so on; in short, a tumbled entanglement of the most different kinds of motion, complicated beyond conception.

And yet, as the ear is able to distinguish all the separate constituent parts of this confused whole, we are forced to conclude that all these different systems of wave coexist in the mass of air, and leave one another mutually undisturbed. But how is it possible for them to coexist, since every individual train of waves has at any particular point in the mass of air its own particular degree of condensation and rarefaction, which determines the velocity of the particles of air to this side or that? It is evident that at each point in the mass of air, at each instant of time, there can be only one single degree of condensation, and that the particles of air can be moving with only one single determinate kind of motion, having only one single determinate amount of velocity, and passing in only one single determinate direction.

What happens under such circumstances is seen directly by the eye in the waves of water. If where the water shews large waves we throw a stone in, the waves thus caused will, so to speak, cut into the larger moving surface, and this surface will be partly raised, and partly depressed, by the new waves, in such a way that the fresh crests of the rings will rise just as much above, and the troughs sink just as much below the curved surfaces of the previous larger waves, as they would have risen above or sunk below the horizontal surface of calm water. Hence where a crest of the smaller system of rings of waves comes upon a crest of the greater system of waves, the surface of the water is raised by the sum of the two heights, and where a trough of the former coincides with a trough of the latter, the surface is depressed by the sum of the two depths. This may be expressed more briefly if we consider the heights of the crests above the level of the surface at rest, as positive magnitudes, and the depths of the troughs as negative magnitudes, and then form the so-called algebraical sum of these positive and negative magnitudes, in which case, as is well known, two positive magnitudes (heights of crests) must be added, and similarly for two negative magnitudes (depths of troughs); but when both negative and positive concur, one is to be subtracted from the other. Performing the addition then in this algebraical sense, we can express our description of the surface of the water on which two systems of waves concur, in the following simple manner: The distance of the surface of the water at any point from its position of rest is at any moment equal to the [algebraical] sum of the distances at which it would have stood had each wave acted separately at the same place and at the same time.

The eye most clearly and easily distinguishes the action in such a case as has been just adduced, where a smaller circular system of waves is produced on a large rectilinear system, because the two systems are then strongly distinguished from each other both by the height and shape of the waves. But with a little attention the eye recognises the same fact even when the two systems of waves have but slightly different forms, as when, for example, long rectilinear waves advancing towards the shore concur with those reflected from it in a slightly different direction. In this case we observe those well-known comb-backed waves where the crest of one system of waves is heightened at some points by the crests of the other system, and at others depressed by its troughs. The multiplicity of forms is here extremely great, and any attempt to describe them would lead us too far. The attentive observer will readily comprehend the result by examining any disturbed surface of water, without further description. It will suffice for our purpose if the first example has given the reader a clear conception of what is meant by adding waves together.^[1]

Hence although the surface of the water at any instant of time can assume only one single form, while each of two different systems of waves simultaneously attempts to impress its own shape upon it, we are able to suppose in the above sense that the two systems coexist and are superimposed, by considering the actual elevations and depressions of the surface to be suitably separated into two parts, each of which belongs to one of the systems alone.

In the same sense, then, there is also a superimposition of different systems of sound in the air. By each train of waves of sound, the density of the air and the velocity and position of the particles of air, are temporarily altered. There are places in the wave of sound comparable with the crests of the waves of water, in which the quantity of the air is increased, and the air, not having free space to escape, is condensed; and other places in the mass of air, comparable to the troughs of the waves of water, having a diminished quantity of air, and hence diminished density. It is true that two different degrees of density, produced by two different systems of waves, cannot coexist in the same place at the same time; nevertheless the condensations and rarefactions of the air can be (algebraically) added, exactly as the elevations and depressions of the surface of the water in the former case. Where two condensations are added we obtain increased condensation, where two rarefactions are added we have increased rarefaction; while a concurrence of condensation and rarefaction mutually, in whole or in part, destroy or neutralise each other.

The displacements of the particles of air are compounded in a similar manner. If the displacements of two different systems of waves are not in the same direction, they are compounded diagonally; for example, if one system would drive a particle of air upwards, and another to the right, its real path will be obliquely upwards towards the right. For our present purpose there is no occasion to enter more particularly into such compositions of motion in different directions. We are only interested in the effect of the mass of air upon the ear, and for this we are only concerned with the motion of the air in the passages of the ear. Now the passages of our ear are so narrow in comparison with the length of the waves of sound, that we need only consider such motions of the air as are parallel to the axis of the passages, and hence have only to distinguish displacements of the particles of air outwards and inwards, that is towards the outer air and towards the interior of the ear. For the magnitude of these displacements as well as for their velocities with which the particles of air move outwards and inwards, the same (algebraical) addition holds good as for the crests and troughs of waves of water.

Hence, when severed sonorous bodies in the surrounding atmosphere, simultaneously excite different systems of waves of sound, the changes of density of the air, and the displacements and velocities of the particles of the air within the passages of the ear, are each equal to the (algebraical) sum of the corresponding changes of density, displacements, and velocities, which each system of waves would have separately produced, if it had acted independently;^[2] and in this sense we can say that all the separate vibrations which separate waves of sound would have produced, coexist undisturbed at the same time within the passages of our ear. After having thus in answer to the first question explained in what sense it is possible for several different systems of waves to coexist on the same surface of water or within the same mass of air, we proceed to determine the means possessed by our organs of sense, for analysing this composite whole into its original constituents.

I have already observed that an eye which surveys an extensive and disturbed surface of water, easily distinguishes the separate systems of waves from each other and follows their motions. The eye has a great advantage over the ear in being able to survey a large extent of surface at the same moment. Hence the eye readily sees whether the individual waves of water are rectilinear or curved, and whether they have the same centre of curvature, and in what direction they are advancing. All these observations assist it in determining whether two systems of waves are connected or not, and hence in discovering their corresponding parts. Moreover, on the surface of the water, waves of unequal length advance with unequal velocities, so that if they coincide at one moment to such a degree as to be difficult to distinguish, at the next instant one train pushes on and the other lags behind, so that they become again separately visible. In this way, then, the observer is greatly assisted in referring each system to its point of departure, and in keeping it distinctly visible during its further course. For the eye, then, two systems of waves having different points of departure can never coalesce; for example, such as arise from two stones thrown into the water at different points. If in any one place the rings of waves coincide so closely as not to be easily separable, they always remain separate during the greater part of their extent. Hence the eye could not be easily brought to confuse a compound with a simple undulatory motion. Yet this is precisely what the ear does under similar circumstances when it separates the musical tone which has proceeded from a single source of sound, into a series of simple partial tones.

But the ear is much more unfavourably situated in relation to a system of waves of sound, than the eye for a system of waves of water. The ear is affected only by the motion of that mass of air which happens to be in the immediate neighbourhood of its tympanum within the aural passage. Since a transverse section of the aural passage is comparatively small in comparison with the length of waves of sound (which for serviceable musical tones varies from 6 inches to 32 feet),^[3] it corresponds to a single point of the mass of air in motion. It is so small that distinctly different degrees of density or velocity could scarcely occur upon it, because the positions of greatest and least density, of greatest positive and negative velocity, are always separated by half the length of a wave. The ear is therefore in nearly the same condition as the eye would be if it looked at one point of the surface of the water, through a long narrow tube, which would permit of seeing its rising and falling, and were then required to undertake an analysis of the compound waves. It is easily seen that the eye would, in most cases, completely fail in the solution of such a problem. The ear is not in a condition to discover how the air is moving at distant spots, whether the waves which strike it are spherical or plane, whether they interlock in one or more circles, or in what direction they are advancing. The circumstances on which the eye chiefly depends for forming a judgment, are all absent for the ear.

If, then, notwithstanding all these difficulties, the ear is capable of distinguishing musical tones arising from different sources — and it really shews a marvelous readiness in so doing — it must employ means and possess properties altogether different from those employed or possessed by the eye. But whatever these means may be — and we shall endeavour to determine them hereafter — it is clear that the analysis of a composite mass of musical tones must in the first place be closely connected with some determinate properties of the motion of the air, capable of impressing themselves even on such a very minute mass of air as that contained in the aural passage. If the motions of the particles of air in this passage are the same on two different occasions, the ear will receive the same sensation, whatever be the origin of those motions, whether they spring from one or several sources.

We have already explained that the mass of air which sets the tympanic membrane of the ear in motion, so far as the magnitudes here considered are concerned, must be looked upon as a single point in the surrounding atmosphere. Are there, then, any peculiarities in the motion of a single particle of air which would differ for a single musical tone, and for a combination of musical tones? We have seen that for each single musical tone there is a corresponding periodical motion of the air, and that its pitch is determined by the length of the periodic time, but that the kind of motion during any one single period is perfectly arbitrary, and may indeed be infinitely various. If then the motion of the air lying in the aural passage is not periodic, or if at least its periodic time is not as short as that of an audible musical tone, this fact will distinguish it from any motion which belongs to a musical tone; it must belong either to noises or to several simultaneous musical tones. Of this kind are really the greater number of cases where the different musical tones have been only accidentally combined, and are therefore not designedly framed into musical chords; nay, even where orchestral music is performed, the method of tempered tuning which at present prevails, prevents an accurate fulfillment of the conditions under which alone the resulting motion of the air can be exactly periodic. Hence in the greater number of cases a want of periodicity in the motion might furnish a mark for distinguishing the presence of a composite mass of musical tones.

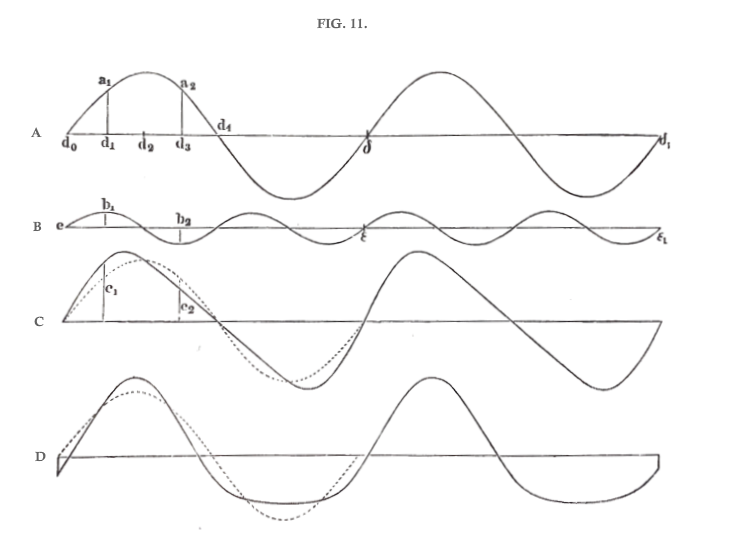
But a composite mass of musical tones may also give rise to a purely periodic motion of the air, namely, when all the musical tones which intermingle, have pitch numbers which are all multiples of one and the same old number, or which comes to the same thing, when all these musical tones, so far as their pitch is concerned, may be regarded as the upper partial tones of the same prime tone. It was mentioned in Chapter I. (p. 22) that the pitch numbers of the upper partial tones are multiples of the pitch number of the prime tone. The meaning of this rule will be clear from a particular example. The curve A, fig. 11, represents a pendular motion in the manner explained in Chap. I. (p. 21), as produced in the air of the aural passage by a tuning-fork in action. The horizontal lengths in the curves of fig. 11, consequently represent the passing time, and the vertical heights the corresponding displacements of the particles of air in the aural passage. Now suppose that with the first simple tone to which the curve A corresponds, there is sounded a second simple tone, represented by the curve B, an Octave higher than the first. This condition requires that two vibrations of the curve B should be made in the same time as one vibration of the curve A. In A, the sections of the curve d₀δ and δ δ₁ are perfectly equal and similar. The curve B is also divided into equal and similar sections e ε and ε ε₁ by the points e, ε, ε₁. We could certainly halve each of the sections e ε and ε ε₁, and thus obtain equal and similar sections, each of which would then correspond to a single period of B. But by taking sections consisting of two periods of B, we divide B into larger sections, each of which is of the same horizontal length, and hence corresponds to the same duration of time, as the sections of A.

If, then, both simple tones are heard at once, and the times of the points e and d₀, ε and δ, ε₁ and δ₁ coincide, the heights of the portions of the section of curve e ε have to be [algebraically] added to heights of the section of curve d₀δ, and similarly for the sections ε ε₁ and δ δ₁. The result of this addition is shewn in the curve C. The dotted line is a duplicate of the section d₀δ in the curve A. Its object is to make the composition of the two sections immediately evident to the eye. It is easily seen that the curve C in every place rises as much above or sinks as much below the curve A, as the curve B respectively rises above or sinks beneath the horizontal line. The heights of the curve C are consequently, in accordance with the rule for compounding vibrations, equal to the [algebraical] sum of the corresponding heights of A and B. Thus the perpendicular c₁ in C is the sum of the perpendiculars a₁ and b₁ in A and B; the lower part of this perpendicular c₁, from the straight line up to the dotted curve, is equal to the perpendicular a₁, and the upper part, from the dotted to the continuous curve, is equal to the perpendicular b₁. On the other hand, the height of the perpendicular c₂ is equal to the height a₂ diminished by the depth of the fall b₂. And in the same way all other points in the curve C are found.^[4]

It is evident that the motion represented by the curve C is also periodic, and that its periods have the same duration as those of A. Thus the addition of the section d₀δ of A and e ε of B, must give the same result as the addition of the perfectly equal and similar sections δ δ₁ and ε ε₁, and, if we supposed both curves to be continued, the same would be the case for all the sections into which they would be divided. It is also evident that equal sections of both curves could not continually coincide in this way after completing the addition, unless the curves thus added could be also separated into exactly equal and similar sections of the same length, as is the case in fig. 11, where two periods of B last as long or have the same horizontal length as one of A. Now the horizontal lengths of our figure represent time, and if we pass from the curves to the real motions, it results that the motion of air caused by the composition of the two simple tones, A and B, is also periodic, just because one of these simple tones makes exactly twice as many vibrations as the other in the same time.

It is easily seen by this example that the peculiar form of the two curves A and B has nothing to do with the fact that their sum C is also a periodic curve. Whatever be the form of A and B, provided that each can be separated into equal and similar sections which have the same horizontal lengths as the equal and similar sections of the other — no matter whether these sections correspond to one or two, or three periods of the individual curves — then any one section of the curve A compounded with any one section of the curve B, will always give a section of the curve C, which will have the same length, and will be precisely equal and similar to any other section of the curve C obtained by compounding any other section of A with any other section of B.

When such a section embraces several periods of the corresponding curve (as in fig. 11, the sections e ε and ε ε₁ each consist of two periods of the simple tone B), then the pitch of this second tone B, is that of an upper partial tone of a prime (as the simple tone A in fig. 11), whose period has the length of that principal section, in accordance with the rule above cited.

In order to give a slight conception of the multiplicity of forms producible by comparatively simple compositions, I may remark that the compound curve would receive another form if the curves B, fig. 11, were displaced a little with respect to the curve A before the addition were commenced. Let B be displaced by being slid to the right until the point e falls under d₁ in A, and the composition will then give the curve D with narrow crests and broad troughs, both sides of the crest being, however, equally steep; whereas in the curve C one side is steeper than the other. If we displace the curve B still more by sliding it to the right till e falls under d₂, the compound curve would resemble the reflection of C in a mirror: that is, it would have the same form as C reversed as to right and left; the steeper inclination which in C lie to the left would now lie to the right. Again, if we displace B till e falls under d₃ we obtain a curve similar to D, fig. 11, but reversed as to up and down, as may be seen by holding the book upside-down, the crests being broad and the troughs narrow.

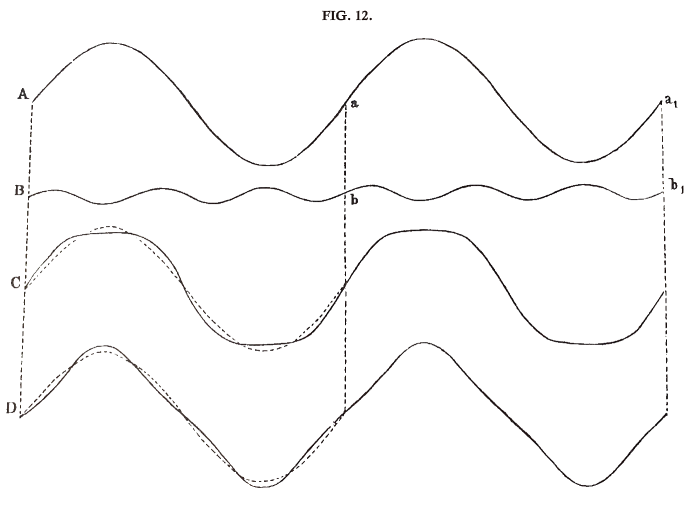
All these curves with their various transitional forms are periodic curves. Other composite periodic curves are shewn at C, D, fig. 12 above, where they are compounded of the two curves A and B, having their periods in the ratio of 1 to 3. The dotted curves are as before copies of the first complete vibration or period of the curve A, in order that the reader may see at a glance that the compound curve is always as much higher or lower than A, as B is higher or lower than the horizontal line. In C, the curves A and B are added as they stand, but for D the curve B has been first slid half a wave's length to the right, and then the addition has been effected. Both forms differ from each other and from all preceding ones. C has broad crests and broad troughs, D narrow crests and narrow troughs.

In these and similar cases we have seen that the compound motion is perfectly and regularly periodic, that is, it is exactly of the same kind as if it proceeded from a single musical tone. The curves compounded in these examples correspond to the motions of single simple tones. Thus, the motions shewn in fig. 11 (on p. 30) might have been produced by two tuning-forks, of which one sounded an Octave higher than the other. But we shall hereafter see that a flute by itself when gently blown is sufficient to create a motion of the air corresponding to that shewn in C or D of fig. 11. The motions of fig. 12 might be produced by two tuning-forks of which one sounded the twelfth of the other. Also a single; closed organ pipe of the narrower kind (the stop called Quintaten^[5]) would give nearly the same motion as that of C or D in fig. 12.

Here, then, the motion of the air in the aural passage has no property by which the composite^[6] musical tone can be distinguished from the single musical tone. If the ear is not assisted by other accidental circumstances, as by one tuning-fork beginning to sound before the other, so that we hear them struck, or, in the other case, the rustling of the wind against the mouthpiece of the flute or lip of the organ pipe, it has no means of deciding whether the musical tone is simple or composite.

Now, in what relation does the ear stand to such a motion of the air? Does it analyse it or does it not? Experience shews us that when two tuning-forks, an Octave or a Twelfth apart in pitch, are sounded together, the ear is quite able to distinguish their simple tones, although the distinction is a little more difficult with these than with other intervals. But if the ear is able to analyse a composite musical tone produced by two tuning-forks, it cannot but be in a condition to carry out a similar analysis, when the same motion of the air is produced by all single flute or organ pipe. And this is really the case. The single musical tone of such instruments, proceeding from a single source, is, as we have already mentioned, analysed into partial simple tones, consisting in each case of a prime tone, and one upper partial tone, the latter being different in the two cases.

The analysis of a single musical tone into a series of partial tones depends, then, upon the same property of the ear as that which enables it to distinguish different musical tones from each other, and it must necessarily effect both analyses by a rule which is independent of the fact that the waves of sound are produced by one or by several musical instruments.

The rule by which the ear proceeds in its analysis was first laid down as generally true by G. S. Ohm. Part of this rule has been already enunciated in the last chapter (p. 23), where it was stated that only that particular motion of the air which we have denominated a simple vibration, for which the vibrating particles swing backwards and forwards according to the law of pendular motion, is capable of exciting in the ear the sensation of a single simple tone. Every motion of the air, then, which corresponds to a composite mass of musical tones, is, according to Ohm's law, capable of being analysed into a sum of simple pendular vibrations, and to each such single simple vibration corresponds a simple lone, sensible to the ear, and having a pitch determined by the periodic time of the corresponding motion of the air.

The proofs of the correctness of this law, the reasons why, of all vibrational forms, only that one which we have called a simple vibration plays such an important part, must be left for Chapters IV. and VI. Our present business is only to gain a dear conception of what the rule means.

The simple vibrational form is inalterable and always the same. It is only its amplitude and its periodic time which are subject to change. But we have seen in figs. 11 and 12 (p. 30 and p. 32) what varied forms the composition of only two simple vibrations can produce. The number of these forms might be greatly increased, even without introducing fresh simple vibrations of different periodic times, by merely changing the proportions which the heights of the two simple vibrational curves A and B bear to each other, or displacing the curve B by other distances to the right or left, than those already selected in the figures. By these simplest possible examples of such compositions, the reader will be able to form some idea of the enormous variety of forms which would result from using more than two simple forms of vibration, each form representing an upper partial tone of the same prime, and hence, on addition, always producing fresh periodic curves. We should be able to make the heights of each single simple vibrational curve greater or smaller at pleasure, and displace each one separately by any amount in respect to the prime, — or, in physical language, we should be able to alter their amplitudes and the difference of their phases; and each such alteration of amplitude and difference of phase in each one of the simple vibrations would produce a fresh change in the resulting composite vibrational form. [See App. XX. sect. M. No. 2.]

The multiplicity of vibrational forms which can be thus produced by the composition of simple pendular vibrations is not merely extraordinarily great: it is so great that it cannot be greater. The French mathematician Fourier has proved the correctness of a mathematical law, which in reference to our present subject may be thus enunciated: Any given regular periodic form of vibration can always be produced by the addition of simple vibrations, having pitch numbers which are once, twice, thrice, four times, &c., as great as the pitch numbers of the given motion.

The amplitudes of the elementary simple vibrations to which the height of our wave-curves corresponds, and the difference of phase, that is, the relative amount of horizontal displacement of the wave-curves, can always be found in every given case, as Fourier has shewn, by peculiar methods of calculation (which, however, do not admit of any popular explanation), so that any given regularly periodic motion can always be exhibited in one single way, and in no other way whatever, as the sum of a certain number of pendular vibrations.

Since, according to the results already obtained, any regularly periodic motion corresponds to some musical tone, and any simple pendular vibration to a simple musical tone, these propositions of Fourier may be thus expressed in acoustical terms:

Any vibrational motion of the air in the entrance to the ear, corresponding to a musical tone, may be always, and for each case only in one single way, exhibited as the sum of a number of simple vibrational motions, corresponding to the partials of this musical tone.

Since, according to these propositions, any form of vibration, no matter what shape it may take, can be expressed as the sum of simple vibrations, its analysis into such a sum is quite independent of the power of the eye to perceive, by looking at its representative curve, whether it contains simple vibrations or not, and if it does, what they are. I am obliged to lay stress upon this point, because I have by no means unfrequently found even physicists start on the false hypothesis, that the vibrational form must exhibit little waves corresponding to the several audible upper partial tones. A mere inspection of the figs. 11 and 12 (p. 30 and p. 32) will suffice to shew that although the composition can be easily traced in the parts where the curve of the prime tone is dotted in, this is quite impossible in those parts of the curve C and D in each figure, where no such assistance has been provided. Or, if we suppose that an observer who had rendered himself thoroughly familiar with the curves of simple vibrations imagined that he could trace the composition in these easy cases, he would certainly utterly fail on attempting to discover by his eye alone the composition of such curves as are shewn in figs. 8 and 9 (p. 21). In these will be found straight lines and acute angles. Perhaps it will be asked how it is possible by compounding such smooth and uniformly rounded curves as those of our simple vibrational forms A and B in figs. 11 and 12, to generate at one time straight lines, and at another acute angles. The answer is, that an infinite number of simple vibrations are required to generate curves with such discontinuities as are there shewn. But when a great many such curves are combined, and are so chosen that in certain places they all bend in the same direction, and in others in opposite directions, the curvatures mutually strengthen each other in the first case, finally producing an infinitely great curvature, that is, an acute angle, and in the second case they mutually weaken each other, so that ultimately a straight line results. Hence we can generally lay it down as a rule that the force or loudness of the upper partial tones is the greater, the sharper the discontinuities of the atmospheric motion. When the motion alters uniformly and gradually, answering to a vibrational curve proceeding in smoothly curved forms, only the deeper partial tones, which lie nearest to the prime tone, have any perceptible intensity. But where the motion alters by jumps, and hence the vibrational curves shew angles or sudden changes of curvature, the upper partial tones will also have sensible force, although in all these cases the amplitudes decrease as the pitch of the upper partial tones becomes higher.^[7]

We shall become acquainted with examples of the analysis of given vibrational forms into separate partial tones in Chapter V.

The theorem of Fourier here adduced shews first that it is mathematically possible to consider a musical tone as a sum of simple tones, in the meaning we have attached to the words, and mathematicians have indeed always found it convenient to base their acoustic investigations on this mode of analysing vibrations. But it by no means follows that we are obliged to consider the matter in this way. We have rather to inquire, do these partial constituents of a musical tone, such as the mathematical theory distinguishes and the ear perceives, really exist in the mass of air external to the ear? Is this means of analysing forms of vibration which Fourier’s theorem prescribes and renders possible, not merely a mathematical fiction, permissible for facilitating calculation, but not necessarily having any corresponding actual meaning in things themselves? What makes us hit upon pendular vibrations, and none other, as the simplest element of all motions producing sound? We can conceive a whole to be split into parts in very different and arbitrary ways. Thus we may find it convenient for a certain calculation to consider the number 12 as the sum 8 + 4, because the 8 may have to be cancelled, but it does not follow that 12 must always and necessarily be considered as merely the sum of 8 and 4. In another case it might be more convenient to consider 12 as the sum of 7 and 5. Just as little does the mathematical possibility, proved by Fourier, of compounding all periodic vibrations out of simple vibrations, justify us in concluding that this is the only permissible form of analysis, if we cannot in addition establish that this analysis has also an essential meaning in nature. That this is indeed the case, that this analysis has a meaning in nature independently of theory, is rendered probable by the fact that the ear really effects the same analysis, and also by the circumstance already named, that this kind of analysis has been found so much more advantageous in mathematical investigations than any other. Those modes of regarding phenomena that correspond to the most intimate constitution of the matter under investigation are, of course, also always those which lead to the most suitable and evident theoretical treatment. But it would not be advisable to begin the investigation with the functions of the ear, because these are very intricate, and in themselves require much explanation. In the next chapter, therefore, we shall inquire whether the analysis of compound into simple vibrations has an actually sensible meaning in the external world, independently of the action of the ear, and we shall really be in a condition to shew that certain mechanical effects depend upon whether a certain partial tone is or is not contained in a composite mass of musical tones. The existence of partial tones will thus acquire a meaning in nature, and our knowledge of their mechanical effects will in turn shed a new light on their relations to the human ear.