Chapter X.

BEATS OF THE UPPER PARTIAL TONES.

The beats hitherto considered, were produced by two simple tones, without any intervention of upper partial or combinational tones. Such beats could only arise when the two given tones made a comparatively small interval with each other. As soon as the interval increased even to a minor Third the beats became indistinct. Now it is well known that beats can also arise from two tones which make a much greater interval with each other, and we shall see hereafter that these beats play a principal part in settling the consonant intervals of our musical scales, and they must consequently be closely examined. The beats heard when the two generating tones are more than a minor Third apart in the scale, arise from upper partial and combinational tones.^[1] When the compound tones have distinctly audible upper partials, the beats resulting from them are generally clearer and stronger than those due to the combinational tones, and it is much more easy to determine their source. Hence we begin the investigation of the beats occurring in wider intervals with those which arise from the presence of upper partial tones. It must not be forgotten, however, that beats of combinational tones are much more general than these, as they occur with all kinds of musical tones, both simple and compound, whereas of course those due to upper partial tones are only found when such partials are themselves distinct. But since all tones which are useful for musical purposes are, with rare exceptions, richly endowed with powerful upper partial tones, the beats due to these upper partials are relatively of much greater practical importance than those due to the weak combinational tones.

When two compound tones are sounded at the same time, it is readily seen, from what precedes, that beats may arise whenever any two upper partial tones lie sufficiently near to each other, or when the prime of one tone approaches to an upper partial of the other. The number of beats is of course, as before, the difference of the vibrational numbers of the two partial tones to which the beats are due. When this difference is small, and the beats are therefore slow, they are relatively most distinct to hear and to count and to investigate, precisely as for beats of prime tones. They are also more distinct when the particular partial tones which generate them are loudest. Now, for the tones most used in music, partials with a low ordinal number are loudest, because the intensity of partial tones usually diminishes as their ordinal number increases.

Let us begin, then, with examples like the following, on an organ in its principal or violin stops,^[2] or upon an harmonium:

The minims in these examples denote the prime tones of the notes struck, and the crotchets the corresponding upper partial tones. If the octave \(C\) \(c\) in the first example is tuned accurately, no beats will be heard. But if the upper note is changed into \(B\) as in the second example, or \(d\flat\) as in the third, we obtain the same beats as we should from the two tones \(B\) \(c\), or \(c\) \(d\flat\) , where the interval is a Semitone. The number of beats (16\(\small{\tfrac{1}{2}}\) in a second) is the same in each case, but their intensity is naturally less in the former case, because they are somewhat smothered by the strong deep tone \(C\), and also because \(c\), the second partial of \(C\), has generally less force than its prime. ^[3]

In examples 4 and 5 beats will be heard on keyed instruments tuned according to the usual system of temperament. If the tempered intonation is exact there will be one beat in a second, ^[4] because the note \(a''\) on the instrument does not exactly agree with the note \(a''\), which is the third partial tone of the note \(d'\). On the other hand the note \(a''\) on the instrument exactly coincides with \(a''\), the second partial tone of the note \(a'\) in the fifth example, so that on instruments exactly tuned in any temperament the two examples 4 and 5 should give the same number of beats. Since the first upper partial tone makes exactly twice as many vibrations in a second as its prime, the \(c\) on the instrument in Ex. 1, is identical with the first upper partial of the prime tone \(C\), provided \(c\) makes twice as many vibrations in a second as \(C\). The two notes \(G\), \(c\), cannot be struck together without producing beats, unless this exact relation is maintained. The least deviation from this exact relation is betrayed by beats. In the fourth example the beats will not cease till we tune \(a''\) on the instrument so as to coincide with the third partial tone of the note \(d\), and this can only happen when the pitch number of \(a''\) is precisely three times that of \(d'\). In the fifth example we have to make the pitch number of \(a'\) half as great as that of \(a''\), which is three times that of \(d'\); that is the pitch numbers of \(d'\) and \(a'\) must be exactly as 2 : 3, or beats will ensue. Any deviation from this ratio will be detected at once by beats.

Now we have already shewn that the pitch numbers of two tones which form an Octave are in the ratio 1 : 2, and those of two which form a Fifth in that of 2 : 3. These ratios were discovered long ago by merely following the judgment of the ear respecting the most pleasant concord of two tones. The circumstances just stated furnish the reason why these intervals when tuned according to these simple ratios of numbers, and in no other case, will produce an undisturbed concord, whereas very small deviations from this mathematical intonation will betray themselves by that restless fluctuation of tone known as beats. The \(d'\) and \(a'\) of the last example, if \(d'\) tuned as a perfect Fifth below \(a\) [that is as \(d_1\) on the Harmonical], make 293\(\small{\tfrac{2}{3}}\) and 440 vibrations in a second respectively, and their common upper partial \(a''\) makes 3 x 293 \(\small{\tfrac{2}{3}}\) = 2 x 440 = 880 vibrations in a second. In the tempered intonation \(d'\) makes almost exactly 293\(\small{\tfrac{2}{3}}\) vibrations in a second, and hence its second upper partial (or third partial) tone makes 881 vib. in the same time, and this extremely small difference is betrayed to the ear by one beat in a second. That imperfect Octaves and Fifths will produce beats, was a fact long known to organ builders, who made use of it practically to obtain the required just or tempered intonation with greater ease and certainty. Indeed, there is no more sensitive means of proving the correctness of intervals.

Two musical tones, therefore, which stand in the relation of a perfect Octave, a perfect Twelfth, or a perfect Fifth, go on sounding uniformly without disturbance, and are thus distinguished from the next adjacent intervals, imperfect Octaves and Fifths, for which a part of the tone breaks up into distinct pulses, and consequently the two tones do not continue to sound without interruption. For this reason the perfect Octave, Twelfth, and Fifth will be called consonant intervals in contradistinction to the next adjacent intervals, which are termed dissonant. Although these names were given long ago, long before anything was known about upper partial tones and their beats, they give a very correct notion of the essential character of the phenomenon which consists in the undisturbed or disturbed coexistence of sounds.

Since the phenomena just described form the essential basis for the construction of normal musical intervals, it is advisable to establish them experimentally in every possible form.

We have stated that the beats heard are the beats of those partial tones of both compounds which nearly coincide. Now it is not always very easy on hearing a Fifth or an Octave which is slightly out of tune recognise clearly with the unassisted ear which part of the whole sound is beating. On listening we are apt to feel that the whole sound is alternately reinforced and weakened. Yet an ear accustomed to distinguish upper partial tones, after directing its attention on the common upper partials concerned, will easily hear the strong beats of these particular tones, and recognise the continued and undisturbed sound of the primes. Strike the note \(d'\) , attend to its upper partial \(a''\), and then strike a tempered Fifth \(a'\) ; the beats of \(a''\) will be clearly heard. To an unpractised ear the resonators already described will be of great assistance. Apply the resonator for \(a''\), and the above beats will be heard with great distinctness. If, on the other hand, a resonator, tuned to one of the prime tones \(d'\) or \(a'\), be employed, the beats are heard much less distinctly, because the continuous part of the tone is then reinforced.

This last remark must not be taken to mean that no other simple tones beat in this combination except \(a''\). On the contrary, there are other higher and weaker upper partials, and also combinational tones which beat, as we shall learn in the next chapter, and these beats coexist with those already described. But the beats of the lowest common upper partials are the most prominent, simply because these beats are the loudest and slowest of all.

Secondly, a direct experimental proof is desirable that the numerical ratios here deduced from the pitch numbers are really those which give no beats. This proof is most easily given by means of the double siren (fig. 56, p. 162). Set the discs in revolution and open the series of 8 holes on the lower and 16 on the upper, thus obtaining two compound tones which form an Octave. They continue to sound without beats as long as the upper box is stationary. But directly we begin to revolve the upper box, thus slightly sharpening or flattening the tone of the upper disc, beats are heard. As long as the box was stationary, the ratio of the pitch numbers was exactly 1 : 2, because exactly 8 pulses of air escaped on one rotation of the lower, and 16 on one rotation of the upper disc. By diminishing the speed of rotation of the handle this ratio may be altered as slightly as we please, but however slowly we turn it, if it move at all, the beats are heard, which shews that the interval is mistuned.

Similarly with the Fifth. Open the series of 12 holes above, and 18 below, and a perfectly unbroken Fifth will be heard as long as the upper windbox is at rest. The ratio of the vibrational numbers, fixed by the holes of the two series, is exactly 2 to 3. On rotating the windchest, beats are heard. We have seen that each revolution of the handle increases or diminishes the number of vibrations of the tone due to the 12 holes by 4 (p. 164c). When we have the tone of 12 holes on the lower discs also, we thus obtain 4 beats. But with the Fifth from 12 and 18 holes each revolution of the handle gives 12 beats, because the pitch number of the third partial tone increases on each revolution of the handle by 3 x 4 = 12, when that of the prime tone increases by 4, and we are now concerned with the beats of this partial tone.

In these investigations the siren has the great advantage over all other musical instruments, of having its intervals tuned according to their simple numerical relations with mechanical certainty by the method of constructing the instrument, and we are consequently relieved from the extremely laborious and difficult measurements of the pitch numbers which would have to precede the proof of our law on any other musical instrument. Yet the law had been already established by such measurements, and the ratios were shewn to approximate more and more closely to those of the simple numbers, as the degree of perfection increased, to which the methods of measuring numbers of vibrations and tuning perfectly had been brought. Just as the coincidences of the two first upper partial tones led us to the natural consonances of the Octave and Fifth, the coincidences of higher upper partials would lead us to a further series of natural consonances. But it must be remarked that in the same proportion that these higher upper partials become weaker, the less perceptible become the beats by which the imperfect are distinguished from the perfect intervals, and the error of tuning is shewn. Hence the delimitation of those intervals which depend upon coincidences of the higher upper partials becomes continually more indistinct and indeterminate as the upper partials involved are higher in order. In the following table the first horizontal line and first vertical column contain the ordinal numbers of the coincident upper partial tones, and at their intersection will be found the name of the corresponding interval between the prime tones, and the ratio of the vibrational numbers of the tones composing it. This numerical ratio always results from the ordinal numbers of the two coincident upper partial tones.

The two lowest lines of this table contain the intervals already considered, the Octave, Twelfth, and Fifth. In the third line from the bottom the 4th partial gives the intervals of the Fourth and double Octave. The 5th partial determines the major Third, either simple or increased by one or two Octaves, and the major Sixth. The 6th partial introduces the minor Third in addition. Here I have stopped, because the 7th partial tone is entirely eliminated, or at least much weakened, on instruments such as the piano, where the quality of tone can be regulated within certain limits.^[5] Even the 6th partial is generally very weak, but an endeavour is made to favour all the partials up to the 5th. We shall return hereafter to the intervals characterised by the 7th partial, and to the minor Sixth, which is determined by the 8th. The following is the order of the consonants intervals beginning with those distinctly characterised, and then proceeding to those which have their limits somewhat blurred, so to speak, by the weaker beats of the higher upper partial tones:—

The following examples in musical notation shew the coincidences of the upper partials. The primes are as before represented by minims, and the upper partials by crotchets. The series of upper partials is continued up to the common tone only.

We have hitherto confined our attention to beats arising from intervals which differ but slightly from those of perfect consonances. When the difference is small the beats are slow, and hence easy both to observe and count. Of course beats continue to occur when the deviation of the two coincident upper partials increases. But as the beats then become more numerous the overwhelming mass of sound of the louder primes conceals their real character more easily than the quicker beats of dissonant primes themselves. These more rapid beats give a rough effect to the whole mass of sound, but the ear does not readily recognise its cause, unless the experiments have been conducted by gradually increasing the imperfection of an harmonic interval, so as to make the beats gradually more and more rapid, thus leading the observer to mark the intermediate steps between the numerable rapid beats on the one hand, and the roughness of a dissonance on the other, and hence to convince himself that the two phenomena differ only in degree.

In the experiments with pairs of simple tones we saw that the distinctness and 1 roughness of their beats depended partly on the magnitude of the interval between the beating tones, and partly upon the rapidity of the beats themselves, so that for high tones this increasing rapidity injured the distinctness of even the beats arising from small intervals, and obliterated them in sensation. At present, as we have to deal with beats of upper partials, which, when their primes lie in the middle region, principally belong to the higher parts of the scale, the rapidity of the beats has a preponderating influence on the distinctness of their definition.

The law determining the number of beats in a second for a given imperfection in a consonant interval, results immediately from the law above assigned for the beats of simple tones. When two simple tones, making a small interval, generate beats, the number of beats in a second is the difference of their vibrational numbers. Let us suppose, by way of example, that a certain prime tone has the pitch number 300. The pitch numbers of the primes which make consonant intervals with it, will be as follows:—

Now assume that the prime tone has been put out of tune by one vibration in a second, so that its pitch number becomes 301, then calculating the vibrational number of the coincident upper partial tones, and taking their difference, we find the number of beats thus:—

Hence the number of beats which arise from putting one of the generating tones out of tune to the amount of one vibration in a second, is always given by the two numbers which define the interval. The smaller number gives the number of beats which arise from increasing the pitch number of the upper tone by 1. The larger number gives the number of beats which arise from increasing the pitch number of the lower tone by 1. Hence if we take the major Sixth \(c\) \(a\), having the ratio 3 : 5, and sharpen \(a\) so as to make one additional vibration in a second, we shall have 3 beats in a second; but if we sharpen \(c\) so as to make one more vibration in a second, we obtain 5 beats in a second and so on.

Our calculation and the rule based on it shew that if the amount by which one of the tones is put out of time remains constant, the number of the beats increases according as the interval is expressed in larger numbers. Hence for Sixths and Thirds the pitch numbers of the tones must be much more nearly in the normal ratio, if we wish to avoid slow beats, than for Octaves and Unisons. On the other hand a slight imperfection in the tuning of Thirds brings us much sooner to the limit where the beats become too rapid to be distinctly separable. If we change the Unison \(c''\) \(c''\), by flattening one of the tones, into the Semitone \(b'\) \(c''\), on sounding the notes together there results a clear dissonance of 33 beats, the number which, as before observed, seems to give the maximum of harshness. But to obtain 33 beats from fifth \(f' c''\), it is only necessary to alter \(c''\) by a quarter of a Tone. If it is changed by a Semitone, so that \(f'\) \(c''\) becomes \(f'\) \(b'\), there result 66 beats, and their clearness is already much injured. To obtain 33 beats the \(c''\) must not be changed in the Fifth \(c''\) \(g''\) by more than one-sixth of a Tone , in the Fourth \(c''\) \(f''\) by more than one-eighth, in the major Third \(c''\) \(e''\) and major Sixth \(c''\) \(a''\) by more than one-tenth, and in the minor Third \(c''\) \(e''\flat\) by more than one-twelfth. Conversely, if in each of these intervals the pitch number of \(c''\) be altered by 33, so that \(c''\) becomes \(b'\) or \(d''\flat\), we obtain the following numbers of beats:—

Now since 99 beats in a second produce very weak effects even under favourable circumstances for simple tones, and 132 beats in a second seem to lie at the limit of audibility, we must not be surprised if such numbers of beats, produced by the weaker upper partials, and smothered by the more powerful prime tones, no longer produce any sensible effect, and in fact vanish so far as the ear is concerned. Now this relation is of great importance in the practice of music, for in the table it will be seen that the mistuned Fifth gives the interval \(b'\) \(g''\), which is much used as an imperfect consonance under the name of minor Sixth. In the same way we find the major Third \(d''\flat\) \(f''\) as a mistuned Fourth, and the Fourth \(b'\) \(e''\) as a mistuned major Third, and so on. That, at least in this part of the scale, the major Third does not produce the beats of a mistuned Fourth, or the Fourth those of a mistuned major Third, is explained by the great number of beats. In point of fact these intervals in this part of the scale give a perfectly uninterrupted sound, without a trace of beats or harshness, when they are tuned perfectly.

This brings us to the investigation of those circumstances which affect the perfection of the consonance for the different intervals. A consonance has been characterised by the coincidence of two of the upper partial tones of the compounds forming the chord. When this is the case the two compound tones cannot generate any slow beats. But it is possible that some other two upper partial tones of these two compounds may be so nearly of the same pitch that they can generate rapid beats. Cases of this kind occur in the last examples in musical notation (p. 183d). Among the upper partials of the major Third \(F A\) occur \(f'\) and \(e'\), side by side; and among those of the minor Third \(F A\flat\), will be found \(a'\) and \(a'\flat\). In each case there is the dissonance of a Semitone, and these must produce the same beats as if they had been given directly as simple prime tones. Now although such beats can produce no very prominent impression, partly on account of their rapidity, partly on account of the weakness of the tones which generate them, and partly because the primes and other partial tones are sounding on at the same time unintermittently, yet they cannot but exert some effect on the harmoniousness of the interval. In the last chapter we found that in certain qualities of tone, where the higher upper partials are strongly developed, sensible dissonances may arise within a single compound tone (p. 178b). When two such musical tones are sounded together, there will be not only the dissonances resulting from the higher upper partial tones in each individual compound, but also those which arise from a partial tone of the one forming a dissonance with a partial tone of the other, and in this way there must be a certain increase in roughness.

An easy method of finding those upper partials in each consonant interval which form dissonances with each other, may be deduced from what has been already stated concerning larger imperfections in tuning consonant intervals (p. 185c, d). We thus found that the major Third might be considered as a mistuned Fourth, and the Fourth again as a mistuned Third. On raising the pitch of a compound tone by a Semitone, we raise the pitch of all its upper partial tones by the same amount. Those upper partials which coincide for the interval of a Fourth, separate by a Semitone when by altering the pitch of one generating tone we convert the Fourth into a major Third, and similarly those which coincide for the major Third differ by a Semitone for the Fourth, as will appear in the following example:—

The 4th and 3rd partial in the Fourth of the first example coincide as \(f'\). But if the Fourth \(B\flat\) sinks, as in the second example, to the major Third \(A\), its 3rd partial \(f'\) sinks also to \(e'\), and forms a dissonance with the 4th partial \(f'\) of \(F\), which was unaltered. On the other hand the 5th and 4th tone of the two compounds, which in the first example formed the dissonance \(a'\) \(b'\flat\), now coincide as \(a'\). In the same way the consonant unison \(a'\) \(a'\) of the second example appears as the dissonance \(a'\) \(a'\flat\) in the third, and the dissonance \(c''\) \(c''\sharp\) in the second becomes the consonant unison \(c''\) \(c''\) in the third.

Hence in each consonant interval those upper partials form a dissonance, which coincide in one of the adjacent consonant intervals^[6] and in this sense we can say, that every consonance is disturbed by the proximity of the consonances next adjoining it in the scale, and that the resulting disturbance is the greater, the lower and louder the upper partials which by their coincidence characterise the disturbing interval, or, in other words, the smaller the number which expresses the ratio of the pitch numbers.

The following table gives a general view of this influence of the different consonances on each other. The partials are given up to the 9th inclusive, and corresponding names assigned to the intervals arising from the coincidence of the higher upper partial tones. The third column contains the ratios of their pitch numbers, which at the same time furnish the number of the order of the coincident partial tones. The fourth column gives the distance of the separate intervals from each other, and the last a measure of the relative strength of the beats resulting from the mistuning of the corresponding interval, reckoned for the quality of tone of the violin.^[7] The degree to which any interval disturbs the adjacent intervals, increases with this last number.^[8]

The most perfect chord is the Unison, for which both compound tones have the same pitch. All its partial tones coincide, and hence no dissonance can occur except such as is contained in each compound separately (p. 178b).

It is much the same with the Octave. All the partial tones of the higher note of this interval coincide with the evenly numbered partials of the deeper, and reinforce them, so that in this case also there can be no dissonance between two upper partial tones, except such as already exists, in a weaker form, among those of the deeper note. A note accompanied by its Octave consequently becomes brighter in quality, because the higher upper partial tones on which brightness of quality depends, are partly reinforced by the additional Octave. But a similar effect would also be produced by simply increasing the intensity of the lower note without adding the Octave; the only difference would be, that in the latter case the reinforcement of the different partial tones would be somewhat differently distributed.

The cases hitherto considered, where the prime of one compound tone coincides with one of the partials of the other, may be termed absolute consonances. The second compound tone introduces no new element, but merely reinforces a part of the other.

Unison and Octave disturb the next adjacent intervals considerably, in the sense assigned to this expression on p. 186d, so that the minor Second \(C\) \(D\flat\), and the major Seventh \(C\) \(B\), which differ from the Unison and Octave by a Semitone respectively, are the harshest dissonances in our scale. Even the major Second \(C\) \(D\), and the minor Seventh \(C\) \(B\flat\) which are a whole Tone apart from the disturbing intervals, must be reckoned as dissonances, although, owing to the greater interval of the dissonant partial tones, they are much milder than the others. In the higher regions of the scale their roughness is materially lessened by the increased rapidity of the beats. Since the dissonance of the minor Seventh is due to the second partial tone, which in most musical qualities of tone is much weaker than the prime, it is still milder than that of the major Second, and hence lies on the very boundary between dissonance and consonance.

To find additional good consonances we must consequently go to the middle of the Octave, and the first we meet is the Fifth. Immediately next to it within the interval of a Semitone there are only the intervals 5 : 7 and 5 : 8 in our table, and these cannot much disturb it, because in all the better kinds of musical tones the 7th and 8th partials are either very weak or entirely absent. The next intervals with stronger upper partials are the Fourth 3 : 4 and the major Sixth 3 : 5. But here the interval is a whole Tone, and if the tones 1 and 2 of the interval of the Octave could produce very little disturbing effect in the minor Seventh, the disturbance by the tones 2 and 3, or by the vicinity of the Fifth to the Fourth and major Sixth must be insignificant, and the reaction of these two intervals with the tones 3 and 4 or 3 and 5 on the Fifth must be entirely neglected. Hence the Fifth remains a perfect consonance, in which there is no sensible disturbance of closely adjacent upper partial tones. It is only in harsh qualities of tone (harmonium, double-bass, violoncello, reed organ pipes) with high upper partial tones, and deep primes, when the number of beats is small, that we remark that the Fifth is somewhat rougher than the Octave.^[9] Hence the Fifth has been acknowledged as a consonance from the earliest times and by all musicians. On the other hand the intervals next adjacent to the Fifth are those which produce the harshest dissonances after those next adjacent to the Octave. Of the dissonant intervals next the Fifth, those in which the Fifth is flattened, that is which lie between the Fifth and Fourth, and are disturbed firstly by the tones 2 and 3, and secondly by the tones 3 and 4, are more decidedly dissonant than those in which the Fifth is sharpened and which lie between the Fifth and major Sixth, because for the latter the second disturbance arises from the tone 3 and the weaker tone 5.^[10] The intervals between the Fifth and Fourth are consequently always considered dissonant in musical practice. But between the Fifth and major Sixth lies the interval of the minor Sixth, which is treated as an imperfect consonance, and owes this preference mainly to its being the inversion of the major Third. On keyed instruments, as the piano, the same keys will strike notes which at one time represent the consonance \(C\) \(A\flat\), and at another the dissonance \(C\) \(G\sharp\).^[11]

Next to the Fifth follow the consonances of the Fourth 3 : 4 and the major Sixth, the chief disturbance of which arises usually from the Fifth. The Fourth is somewhat further from the Fifth (the interval is 8 : 9) than the major Sixth is (the interval is 9 : 10), and hence the major Sixth is a less perfect consonance than the Fourth. But close by the Fourth lies the major Third with the 4th and 5th partials coincident, and hence when these partials are strongly developed, the Fourth may lose its advantage over the major Sixth. It is also well known that the old theoretical musicians long disputed as to whether the Fourth should be considered consonant or dissonant. The precedence given to the Fourth over the major Sixth and major Third, is rather due to its being the inversion of the Fifth than to its own inherent harmoniousness. The Fourth, the major Sixth and minor Sixth, are rendered less pleasant by being widened by an Octave (thus becoming the Eleventh, and major and minor Thirteenth), because they then lie near the Twelfth, and consequently the disturbance by the characteristic tones of the Twelfth 1 and 3, is greater, and hence also the adjacent intervals 2 : 5 for the Eleventh, and 2 : 7 for the Thirteenth, are more disturbing than are the 4 : 5 for the Fourth and the 4 : 7 for the Sixth in the lower Octave.^[12]

Next in the order of the consonances come the major and minor Third. The latter is very imperfectly delimited on instruments which, like the pianoforte, do not strongly develop the 6th partial of the compound tone, because it can then be imperfectly tuned without producing sensible beats.^[13] The minor Third is sensibly exposed to disturbance from the Unison, and the major Third from the Fourth; and both mutually disturb each other, the minor Third coming off worse than the major. For the harmoniousness of either interval it is necessary that the disturbing beats should be very rapid. Hence in the upper part of the scale these intervals are pure and good, but in the lower part they are very rough. All antiquity, therefore, refused to accept Thirds as consonances. It was not till the time of Franco of Cologne (at the end of the twelfth century) that they were admitted as imperfect consonances. The reason of this may probably be that musical theory was developed among classical nations and in medieval times principally in respect to men’s, voices, and in the lower part of this scale Thirds are far from good. With this we must connect the fact that the proper intonation of major Thirds was not discovered in early times, and that the Pythagorean Third, with its ratio of 64 : 81, was looked upon as the normal form till towards the close of the middle ages.

The important influence exercised on the harmoniousness of the consonances, especially the less perfect ones, by the rapidity of the weak beats of the dissonant upper partials, has already been indicated. If we place all the intervals above the same bass note, the number of their beats in a second varies much, and is much greater for the imperfect than for the perfect consonances. But we can give all the intervals hitherto considered such a position in the scale that the number of their beats in a second should be the same. Since we have found that 33 beats in a second produce about the maximum amount of roughness, I have so chosen the position of the intervals in the following examples in musical notation, as to give^[15] that number in every ease. The intonation is supposed to be that of the scale of \(C\) major with just intervals, but \(b\flat\) represents the subminor Seventh of \(c\) (4 : 7).^[16]

The prime tones of the notes in this example are all partials of \(C_{\prime}\) which makes 33 vibrations in a second, and hence their own pitch numbers and those of their upper partials are multiples of 33; consequently the difference of these pitch numbers, which gives the number of beats, must always be 33, 66, or some higher multiple of 33.

In the low positions here assigned the beats arising from the dissonant upper partials are as effective as their intensity will allow, and in this case the Sixths, Thirds, and even the Fourth are considerably rough. But the major Sixth and major Third shew their superiority over the minor Third and minor Sixth, by descending lower down in the scale, and yet sounding somewhat milder than the others. It is also a well-known practical rule among musicians to avoid these close intervals in low positions, when soft chords are required, though there was no justification for this rule in any previous theory of chords.

My theory of hearing by means of the sympathetic vibration of elastic appendages to the nerves, would allow of calculating the intensity of the beats of the different intervals, when the intensity of the upper partials in the corresponding quality of tone belonging to the instrument used, is known, and the intervals are so chosen that the number of beats in a second is the same. But such a calculation would be very different for different qualities of tone, and holds only for such a particular case as may be assumed.

For intervals constructed on the same lower note a new factor comes into play, namely, the number of beats which occur in a second; and the influence of this factor on the roughness of the sensation cannot be calculated directly by any fixed law. 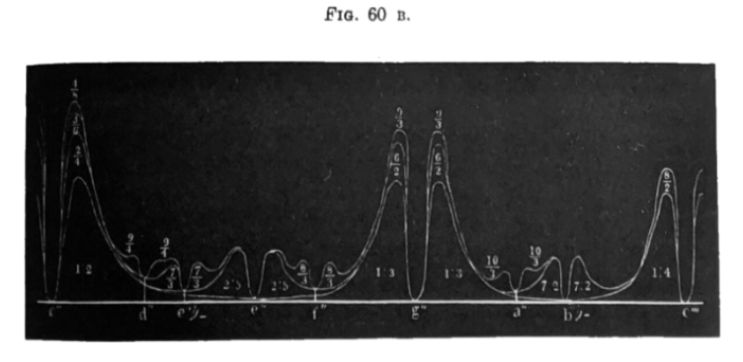But to obtain a general graphical representation of the complicated relations which co-operate to produce the effect, I have made such a calculation, knowing that diagrams teach more at a glance than the most complicated descriptions, and have hence constructed figs. 60, A and B (p. 193). In order to construct them I have been forced to assume a somewhat arbitrary law for the dependence of roughness upon the number of beats. I chose for this purpose the simplest mathematical formula which would shew that the roughness vanishes when there 5) are no beats, increases to a maximum for 33 beats, and then diminishes as the number of beats increases. Next I have selected the quality of tone on the violin in order to calculate the intensity and roughness of the beats due to the upper partials taken two and two together, and from the final results I have constructed figs. 60, A and B, opposite. The base lines \(c'\) \(c''\), \(c''\) \(c'''\) denote those parts of the musical scale which lie between the notes thus named, but the pitch is taken to increase continuously [as when the finger slides down the violin string], and not by separate steps [as when the finger stops off definite lengths of the violin string]. It is further assumed that the notes or compound tones belonging to any individual part of the scale, are sounded together with the note \(c'\), which forms the constant lower note of all the intervals. Fig. 60 A, therefore, shews the roughness of all intervals which are less than an Octave, and fig. 60 B of those which are greater than one Octave, and less than two. Above the base line there are prominences marked with the ordinal numbers of the partials. The height of these prominences at every point of their width is made proportional to the roughness produced by the two partial tones denoted by the numbers, when a note of corresponding pitch is sounded at the same time with the note \(c'\). The roughnesses produced by the different pairs of upper partials are erected one over the other.^[17] It will be seen that the various roughnesses arising from the different intervals encroach on each other’s regions, and that only a few narrow valleys remain, corresponding to the position of the best consonances, in which the roughness of the chord is comparatively small. The deepest valleys in the first Octave \(c'\) \(c''\) belong to the Octave \(c'\) and the Fifth \(g'\); then comes the Fourth \(f'\), the major Sixth \(a'\), and the major Third \(e'\), in the order already found for these intervals. The minor Third \(e'\flat\), and the minor Sixth \(a'\flat\), have 'cols' rather than valleys, the bottoms of their

depressions lie so high, corresponding to the greater roughness of these intervals. They are almost the same as for the intervals involving 7, as 4 : 7, 5 : 7, 6 : 7.^[18]

In the second Octave as a general rule all those intervals of the first Octave are improved, in which the smaller of the two numbers expressing the ratio was even; thus the Twelfth 1 : 3 or \(c'\)\(g''\) , major Tenth 2 : 5 or \(c'\)\(e''\), subminor Fourteenth 2 : 7 or \(c'\)\(b''\flat\)— and subminor Tenth 3 : 7 or \(c'\)\(e''\flat\)- are smoother than the Fifth 2 : 3 or \(c'\)\(g'\), major Third 4 : 5 or \(c'\)\(e'\), subminor Seventh 4 : 7 or \(c'\)\(b'\flat\)-, and subminor Third 6 : 7 or \(c'\)\(e'\flat\)—. The other intervals are relatively deteriorated. The Eleventh or \(c'\)\(f''\) or increased Fourth is distinctly worse than the major Tenth or \(c'\)\(e''\); the major Thirteenth or \(c'\)\(a''\), or increased major Sixth, is similarly worse than the subminor Fourteenth \(c'\)\(d''\flat\)— . The minor Third or \(c'\)\(e'\flat\), when increased to a minor Tenth or \(c'\)\(e''\flat\),^[19] and the minor Sixth or \(c'\)\(a'\flat\), when increased to a minor Thirteenth or \(c\) \(a''\flat\), fare still worse, on account of the increased disturbance of the adjacent intervals. The conclusions here drawn from calculation are easily confirmed by experiments on justly intoned instruments.^[20] That they are also attended to in the practice of musical composition, notwithstanding the theoretical assumption that the nature of a chord is not changed by altering the pitch of any one of its constituents by whole octaves, we shall see further on, when considering chords and their inversions.

It has already been mentioned that peculiarities of individual qualities of tone may have considerable effect in altering the order of the relative harmoniousness of the intervals. The quality of tone in the musical instruments now in use has been of course selected and altered with a view to its employment in harmonic combinations. The preceding investigation of the qualities of tone in our principal musical instruments has shewn that in what are considered good qualities of tone the Octave and Twelfth of the prime, that is the 2nd and 3rd partials, are powerful, the 4th and 5th partials have only moderate strength, and the higher partials rapidly diminish in force. Assuming such a quality of tone, the results of this chapter may be summed up as follows.

When two musical tones are sounded at the same time, their united sound is generally disturbed by the beats of the upper partials, so that a greater or less part of the whole mass of sound is broken up into pulses of tone, and the joint effect is rough. This relation is called Dissonance.

But there are certain determinate ratios between pitch numbers, for which this rule suffers an exception, and either no beats at all are formed, or at least only such as have so little intensity that they produce no unpleasant disturbance of the united sound. These exceptional cases are called Consonances.

1. The most perfect consonances are those that have been here called absolute, in which the prime tone of one of the combined notes coincides with some partial tone of the other. To this group belong the Octave , Twelfth , and double Octave .

2. Next follow the Fifth and the Fourth , which may be called perfect consonances, because they may be used in all parts of the scale without any important disturbance of harmoniousness. The Fourth is the less perfect consonance and approaches those of the next group. It owes its superiority in musical practice simply to its being the defect of a Fifth from an Octave, a circumstance to which we shall return in a later chapter.

3. The next group consists of the major Sixth and the major Third , which may be called medial consonances. The old writers on harmony considered them as imperfect consonances. In lower parts of the scale the disturbance of the harmoniousness is very sensible, but in the higher positions it disappears, because the beats are too rapid to be sensible. But each, in good musical qualities of tone, is independently characterised, by the fact that any little defect in its intonation produces sensible beats of the upper partials, and consequently each interval is sharply separated from all adjacent intervals.

4. The imperfect consonances, consisting of the minor Third and minor Sixth , are not in general independently characterised, because in good musical qualities of tone the partials on which their definition depends are often not found for the minor Third, and are generally absent for the minor Sixth, so that small imperfections in the intonation of these intervals do not necessarily produce beats.^[21] They are all less suited for use in lower parts of the scale than the others, and they owe their precedence as consonances over many other intervals which lie on the boundaries of consonance and dissonance, essentially to their being indispensable in the formation of chords, because they are defects of the major Sixth and major Third from the Octave or Fifth. The subminor Seventh 4 : 7 or \(c'\)\(b'\flat\)- is very often more harmonious than the minor Sixth 5 : 8 or \(c'\)\(a'\flat\) , in fact it is always so when the third partial tone of the note is strong as compared with the second, because then the Fifth has a more powerfully disturbing effect on the intervals distant from it by a Semitone, than the Octave on the subminor Seventh, which is rather more than a whole Tone removed from it.^[22] But this subminor Seventh when combined with other consonances in chords produces intervals which are all worse than itself, as 6 : 7, 5 : 7, 7 : 8, &c., and it is consequently not used as a consonance in modern music.^[23]

5. By increasing the interval by an Octave, the Fifth \(c'\)\(g'\) and major Third \(c'\)\(e'\) are improved on becoming the Twelfth \(c'\)\(g''\) and major Tenth \(c'\)\(e''\) . But the Fourth \(c'\)\(f'\) and major Sixth \(c'\)\(a'\) become worse as the Eleventh \(c'\)\(f''\) and major Thirteenth \(c'\)\(a''\). The minor Third \(c'\)\(e'\flat\) and minor Sixth \(c'\)\(a'\flat\), however, become still worse as the minor Tenth \(c\) \(e''\) and minor Thirteenth \(c'\)\(a''\flat\), so that the latter intervals are far less harmonious than the subminor Tenth 3 : 7, \(c'\) \(e''\flat\)-[or \(g\) \(^7b'\flat\)], and subminor Fourteenth 2 : 7, \(c'\)\(b''\flat\)- .

The order of the consonances here proposed is based upon a consideration of the harmoniousness of each individual interval independently of any connection with other intervals, and consequently without any regard to key, scale, and modulation. Almost all writers on musical theory have proposed similar orders for the consonances, agreeing in their general features with each other and with that here deduced from the theory of beats. Thus all put the Unison and Octave first, as the most perfect of all consonances; and next in order comes the Fifth, after which the Fourth is placed by those who do not include the modulational properties of the Fourth, but restrict their observation to the independent harmoniousness of the interval. There is great diversity, on the other hand, in the arrangement of the Sixths and Thirds. The Greeks and Romans did not acknowledge these intervals to be consonances at all, perhaps because in the unaccented Octave, within which their music, arranged for men’s voices, usually lay, these intervals really sound badly, and perhaps because their ear was too sensitive to endure the trifling increase of roughness generated by compound tones when sounded together in Thirds and Sixths. In the present century, the Archbishop Chrysanthus of Dyrrhachium declares that modern Greeks have no pleasure in polyphonic music, and consequently he disdains to enter upon it in his book on music, and refers those who are curious to know its rules, to the writings of the West.^[24] Arabs are of the same opinion according to the accounts of all travellers.

This rule remained in force even during the first half of the middle ages, when the first attempts were made at harmonies for two voices. It was not till towards the end of the twelfth century that Franco of Cologne included the Thirds among the consonances. He distinguishes:—

1. Perfect Consonances: Unison and Octave.

2. Medial Consonances: Fifth and Fourth.

3. Imperfect Consonances: Major and minor Thirds.

4. Imperfect Dissonances: Major and minor Sixth.

5. Perfect Dissonances: Minor Second, augmented Fourth, major and minor Seventh.^[25]

It was not till the thirteenth and fourteenth centuries that musicians began to include the Sixths among the consonances. Philipp de Vitry and Jean de Muris^[26] mention as perfect consonances the Unison, Octave, and Fifth; as imperfect, the Thirds and Sixths. The Fourth has been cut out. The first author opposes the major Third and major Sixth, as more perfect, to the minor Third and minor Sixth. The same order is found in the Dodecachordon of Glareanus, 1557,^[27] who merely added the intervals increased by an Octave. The reason why the Fourth was not admitted as either a perfect or an imperfect consonant, must be looked for in the rules for the progression of parts. Perfect consonances were not allowed to follow each other between the same parts, still less dissonances; but imperfect consonances, as the Thirds and Sixths, were permitted to do so. But on the other hand the perfect consonances, Octaves, and Fifths were admitted in chords on which the music paused, as in the closing chord. Here, however, the Fourth of the bass could not occur because it does not occur in the triad of the tonic. Again a succession of Fourths for two voices was not admitted, as the Fourth and Fifth were too closely related for such a purpose. Hence so far as the progression of parts was concerned, the Fourth shared the properties of dissonances, and it was at once placed among them; but it would have been better to have placed it in an intermediate class between perfect and imperfect consonances. As far as harmoniousness is concerned, there can be no doubt that, for most qualities of tone, the Fourth is much superior to the major Third and major Sixth, and beyond all doubt better than the minor Third and minor Sixth. But the Eleventh, or Fourth increased by an Octave, sounds far from well when the third partial tone is in any degree strong.^[28]

The dispute as to the consonance or dissonance of the Fourth has been continued to the present day. As late as 1840, in Dehn’s treatise on harmony we find it asserted that the Fourth must be treated and resolved as a dissonance; but Dehn certainly puts a totally different interpretation on the question in dispute by laying it down that the Fourth of any bass within its key and independently of the intervals with which it is combined, has to be treated as a dissonance. Otherwise it has been the constant custom in modern music to allow the reduplication of the tonic to occur as the Fourth of the dominant in conjunction with the dominant even in final chords, and it was long so used in these chords, even before Thirds were allowed in them, and in this way it came to be recognised as one of the superior consonances.^[29]